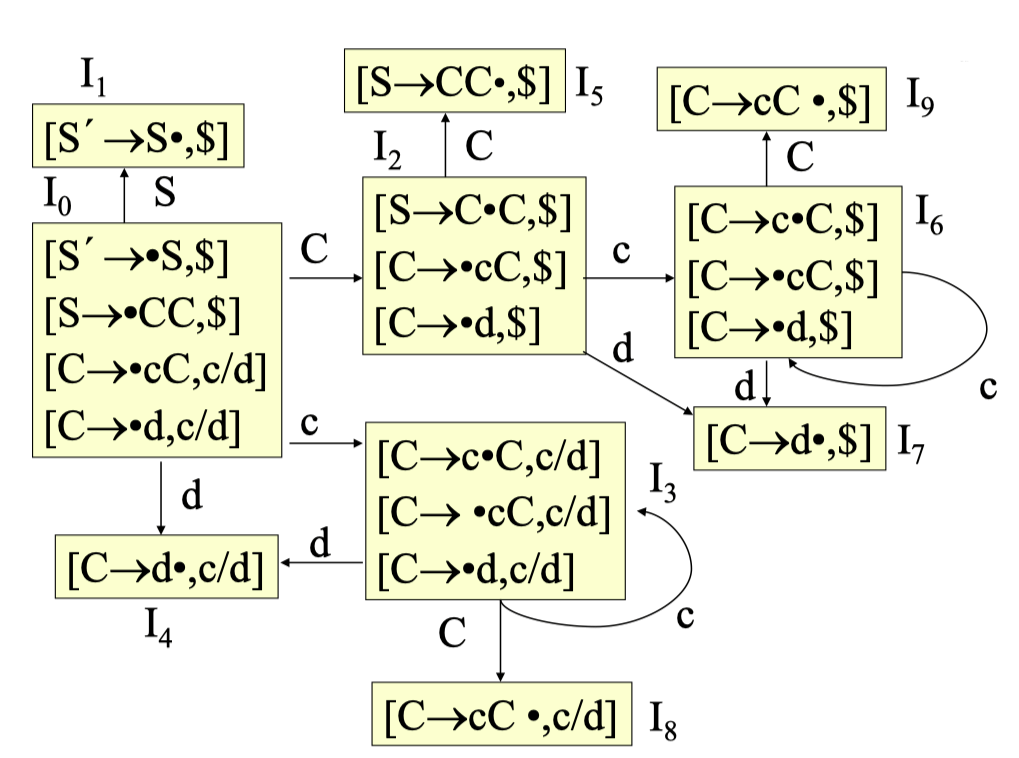语法分析 IV

LR (1) 文法

LR (k) 项

形式：$[A \rightarrow \alpha \cdot \beta, a_1a_2 \ldots a_k]$

• 当 $\beta \neq \varepsilon$ 时，为移进或待归约项，$a_1a_2 \ldots a_k$ 不直接起作用
• 当 $\beta = \varepsilon$ 时，即为归约项 $[A \rightarrow \alpha \cdot, a_1a_2 \ldots a_k]$，仅当前输入符串前 $k$ 个符号是 $a_1a_2 \ldots a_k$ 时，才能用 $A \rightarrow \alpha$ 进行归约
• $a_1a_2 \ldots a_k$ 称为向前搜索符号串（展望项）

LR (1) 有效项

LR (1) 项 $[A \rightarrow \alpha \cdot \beta, a]$ 对于一个可行前缀 $\gamma$ 有效的条件是存在一个推导：

其中：

1. $\gamma = \delta \alpha$
2. 要么 $a$ 是 $w$ 的第一个符号，要么 $w$ 为 $\varepsilon$ 且 $a$ 等于 $\$$

考虑文法 $G:S \rightarrow CC \quad C \rightarrow cC \mid d$

规范推导：

$$S \Rightarrow_{rm}^* ccCcd \Rightarrow_{rm} cccCcd$$

项 $[C \rightarrow c \cdot C, c]$ 对可行前缀 $ccc$ 是有效的。

LR (1) 有效项的推导

若项 $[A \rightarrow \alpha \cdot B \beta, a]$ 对可行前缀 $\gamma = \delta \alpha$ 是有效的，则存在一个规范推导：

假定 $\beta ax \Rightarrow_{rm}^* by$，则对每一个形如 $B \rightarrow \xi$ 的产生式，有规范推导：

从而项 $[B \rightarrow \cdot \xi, b]$ 对于可行前缀 $\gamma = \delta \alpha$ 也是有效的。

注意到 $b$ 必然属于二者之一：

1. 从 $\beta$ 推出的第一个终结符号
2. $\beta \Rightarrow_{rm}^* \varepsilon$ 而 $b = a$

这两种可能性结合在一起，则 $b \in \text{First}(\beta a)$。

LR (1) 项集的构造

构造有效 LR (1) 项集族的方法实质上和构造规范 LR (0) 项集族的方法相同。

我们只需要修改两个过程：Closure 和 Goto。

Closure

设 $I$ 是 $G$ 的一个 LR (1) 项集，$\text{Closure}(I)$ 是从 $I$ 出发用以下三条规则构造的项集：

1. 每一个 $I$ 中的项都属于 $\text{Closure}(I)$
2. 若项 $[A \rightarrow \alpha \cdot B \beta, a]$ 属于 $\text{Closure}(I)$ 且 $B \rightarrow \gamma \in P$，则对任何 $b \in \text{First}(\beta a)$，把 $[B \rightarrow \cdot \gamma, b]$ 加到 $\text{Closure}(I)$ 中
3. 重复执行 (2) 直到 $\text{Closure}(I)$ 不再增大为止

Goto

设 $I$ 是 $G$ 的一个 LR (1) 项集，$X$ 是一个文法符号，定义：

其中 $J = \{[A \rightarrow \alpha X \cdot \beta, a] \mid [A \rightarrow \alpha \cdot X \beta, a] \in I\}$

LR (1) 项集族的构造方法

输入：一个增广文法 $G'$。

输出：LR (1) 项集族，其中的每个项集对文法 $G'$ 的一个或多个可行前缀有效。

方法：过程 Closure 和 Goto，以及用于构造项集的主例程 items。

过程 Closure

过程 Goto

最后执行 $\text{Closure}$ 的原因是，$\text{Goto}$ 函数返回的是一个新的项集，需要对其进行闭包操作。

项集族 $C$

构造 LR (1) 分析表

1. DFA 状态对应分析表行：

   DFA 中的每个状态对应分析表中的一行。

2. DFA 状态转移：

   对于 DFA 中的每一个从状态 $i$ 到状态 $j$ 的转移：

   • 如果转移符号为终结符 $a$：在表项 $M[i, a]$ 中填写 移进动作 $S_j$ （Shift，Action 列）
   • 如果转移符号为非终结符 $A$：在表项 $M[i, A]$ 中填写 转移到状态 $j$ （Goto 列）

3. 包含归约项 $[A \rightarrow \alpha \cdot, a]$ 的状态 $i$：

   在表项 $M[i, a]$ 中填写归约动作 $r_k$（Reduce），其中 $k$ 是产生式 $A \rightarrow \alpha$ 的编号

注意：如果每个单元格中只包含一个动作，则分析表合法。

LR（1）分析表举例

文法：

项集族：

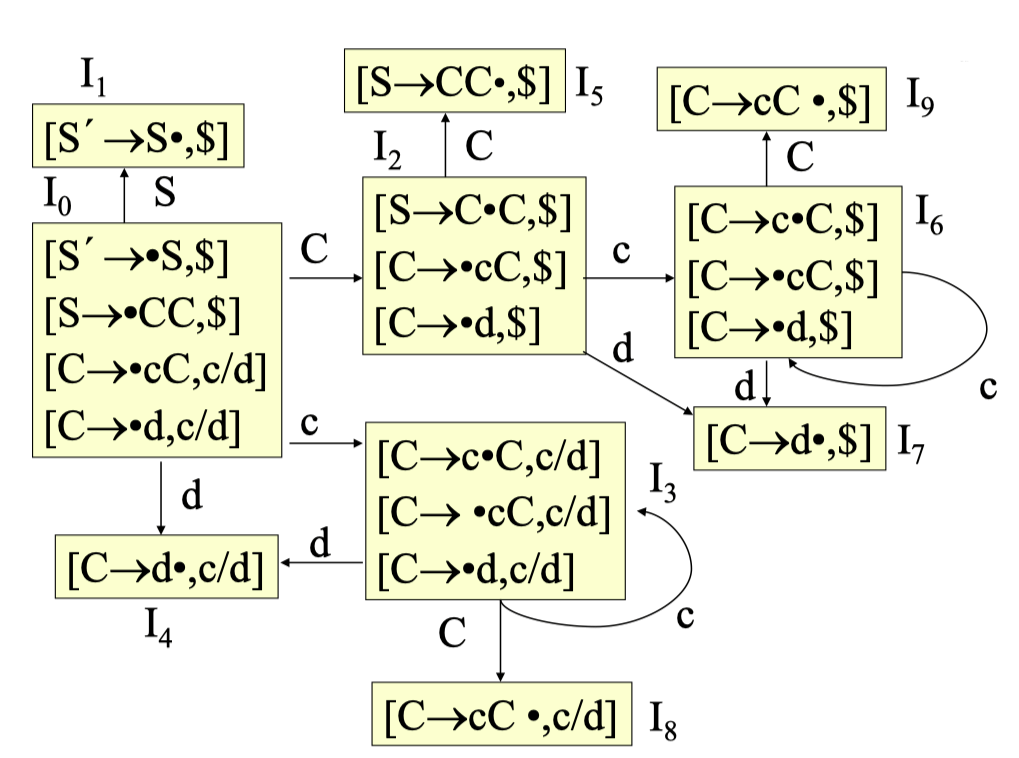
分析表：

LALR 文法

LALR：Look-Ahead LR

LR (1) 分析表：状态多，实际使用较少。

同心集：两个 LR (1) 项集 去掉搜索符后相同，称为 同心。

LALR (1) 分析表：合并同心集（合并搜索符串）后构造出的 LR 分析表。

合并同心项集不会产生移进 / 归约冲突，但是有可能产生归约 / 归约冲突。

因为合并的时候合并的是同心项的展望符，而展望符只在规约的时候起作用，在移入的时候是不起作用的，只要合并前各个同心项目集本身是没有移进 / 归约冲突的，就不会有移进 / 归约冲突（后文有证明）。

LALR 分析表的高效构造算法

通过先构造 LR (1) 分析表再合并得到 LALR (1) 分析表的过程太慢了。

1. 内核项表示：

   使用内核项表示 LR (0) 或 LR (1) 项集。

   内核项：$[S' \rightarrow \cdot S]$ 或 $[S' \rightarrow \cdot S, \$]$，以及 $\cdot$ 不在最左边的项（这些项代表对于已经读入的符号完全没有要求）。

2. 传播和自发生成：

   通过传播和自发生成，获得向前看符号，得到 LALR (1) 内核项。

   传播 / 自发生成：向前看符号的传递过程。

   对于某个项 $[A \rightarrow \alpha \cdot B \beta, a]$ 执行闭包：

   传播：假设向前看符号是一个不在文法中的符号 $\#$，即对 $[A \rightarrow \alpha \cdot B \beta, \#]$ 进行闭包，若得到的某些项的向前看符号 就是 $\#$，那么就认为这些项的向前看符号是传播得到的，直接复制 $a$，就行；

   自发生成：假设向前看符号是一个不在文法中的符号 $\#$，即对 $[A \rightarrow \alpha \cdot B \beta, \#]$ 进行闭包，若有些项的向前看符号 不是 $\#$，那么就认为这些项的向前看符号是传播得到的，不改动这些项的向前看符号；

3. Closure 函数：

   使用 $\text{Closure}$ 函数求出内核项的闭包，得到 LALR 分析表。

由于传播和自发生成的表述比较抽象，这里给一个例子（书 P175）来自己悟：

文法：

直接根据产生式，构建出只有内核项的项集族：

使用如下算法来确定向前看符号：

输入：一个 LR (0) 项集 $I$ 的内核 $K$ 以及一个文法符号 $X$。$\#$ 是一个不在文法中的符号。

输出：由 $I$ 中的项为 $\text{Goto}(I, X)$ 中内核项自生成的向前看符号，以及 $I$ 中将其向前看符号传播到 $\text{Goto}(I, X)$ 中内核项的项。

当我们将算法应用于项集 $I_0$ 的内核时，我们首先计算 $\text{Closure}(\{[S' \rightarrow \cdot S, \#]\})$，得到：

在这个闭包的项中，我们看到有两个项中的向前看符号 $=$ 是自发生成的；

而对于这个闭包结果，把 $\#$ 替换为真实的闭包前原始项 $[S' \rightarrow \cdot S, \$]$ 的向前看符号，即 $\$$，我们认为此时的向前看符号 $\$$ 是传播得到的。

LALR (1) 的讨论

1. 核心依赖性：

   由于 $\text{Goto}(I, X)$ 仅依赖于 $I$ 的核心，因此 LALR（1）项集合并后的转换函数 $\text{Goto}(I, X)$ 随自身的合并而得到

2. 动作修改：

   动作 $\text{action}$ 应当进行修改，以反映各被合并集合的既定动作

3. 归约 - 归约冲突：

   项集合合并时，可能会导致冲突。这种冲突不会是移进 - 归约冲突：

   $$\begin{aligned} I_k: &\{[A \rightarrow \alpha \cdot, u_1] \quad [B \rightarrow \beta \cdot ay, b]\} \quad a \cap u_1 = \varnothing \\ I_j: &\{[A \rightarrow \alpha \cdot, u_2] \quad [B \rightarrow \beta \cdot ay, c]\} \quad a \cap u_2 = \varnothing \\ I_{kj}: &\{[A \rightarrow \alpha \cdot, u_1 \cup u_2] \quad [B \rightarrow \beta \cdot ay, b/c]\} \quad a \cap (u_1 \cup u_2) = \varnothing \end{aligned}$$

   但可能引起归约 - 归约冲突：

   $$\begin{aligned} I_k: &\{[A \rightarrow \alpha \cdot, u_1] \quad [B \rightarrow \beta \cdot, u_2]\}\\ I_j: &\{[A \rightarrow \alpha \cdot, u_2] \quad [B \rightarrow \beta \cdot, u_1]\}\\ I_{kj}: &\{[A \rightarrow \alpha \cdot, u_1 \cup u_2] \quad [B \rightarrow \beta \cdot, u_1 \cup u_2]\} \end{aligned}$$

   此时，有两个展望符号相同、核心也相同的归约项，可能产生归约 - 归约冲突。

二义性文法的使用

1. 二义性文法不是 LR 的
2. 有用的二义性文法：
   • 简洁描述某些结构
   • 隔离某些语法结构，对其进行特殊处理
3. 处理某些二义性文法：
   • 通过消除二义性规则，保证每个句子只有一棵语法分析树
   • 可以在 LR 分析器中实现这一规则

利用优先级 / 结合性消除冲突

1. 二义性文法：
   • $E \rightarrow E + E \mid E * E \mid (E) \mid \text{id}$
   • 等价于：$E \rightarrow E + T \mid T \quad T \rightarrow T * F \mid F \quad F \rightarrow (E) \mid \text{id}$
2. 二义性文法的优点：
   • 容易：修改算符的优先级和结合性
   • 简洁：多优先级无需引入大量非终结符
   • 高效：不需处理 $E \rightarrow T$ 这样的归约

四种 LR 解析的对比

1. 如果构造 LR (0) 的 DFA
   • 没有归约冲突就是 LR (0) 文法
   • 有冲突但可以通过 Follow 集合解决冲突就是 SLR 文法
   • 否则不是 SLR 文法
2. 如果构造 LR (1) 的 DFA
   • 没有冲突就是 LR (1) 文法
   • 如果合并同心集之后也没有冲突，那么就是 LALR (1) 文法
3. 包含关系
   • $\text{LR(0)} < \text{SLR} < \text{LALR} < \text{LR(1)}$

用途比较：

• $\text{LR}(0)$：最简单，但只能用于最简单的文法
• $\text{SLR}$：构造简单，易于实现，实用价值高（大多数上下文无关文法均可构造 SLR 分析表）
• $\text{LR}(1)$：适用文法类最大（几乎所有上下文无关文法），但分析表体积过大，使用价值不大
• $\text{LALR}(1)$：介于 $\text{SLR}$ 和 $\text{LR}(1)$ 之间，最实用（比 $\text{SLR}$ 适用更多，比 $\text{LR}(1)$ 更简单）