语法分析 III

自底向上语法分析

自底向上语法分析：将一个串 $w$ 归约回到文法开始符号 $S$ 的过程。

在每个归约（reduction）步骤中，一个与某 产生式右部相匹配的特定子串 被替换为该 产生式左部 的非终结符号。

下文中，对如下概念不加区分：

产生式左部 / 产生式头
产生式右部 / 产生式体

归约：是一个推导步骤的反向操作

推导步骤：将句型中的一个非终结符号替换为该符号的某个产生式的体 $A \rightarrow \alpha$
归约步骤：与某产生式体匹配的子串被替换为该产生式头部的非终结符号 $\alpha \leftarrow A$

自底向上语法分析的目标

目标：反向构造一个推导过程。

方法：对输入进行从左到右的扫描，并在扫描过程中进行自底向上语法分析，就可以反向构造出一个最右推导。

句柄（Handle）

句柄：是与某个 产生式体 匹配的子串，对它的归约代表了相应的最右推导中的一个反向步骤（看接下来的形式定义会好理解一些）。

Ref：
前缀（prefix）：移走 $x$ 尾部的零个或多个连续的符号。
后缀（suffix）：移走 $x$ 头部的零个或多个连续的符号。
子串（substring）：从 $x$ 中删去一个前缀和一个后缀。

注意，和某个产生式体匹配的最左子串不一定是句柄（ 需要归约后能回到开始符号 ）。

形式定义

若有 $S {\Rightarrow}^{*}_{\text{rm}} \alpha A w \Rightarrow_{\text{rm}} \underbrace{\alpha \beta w}_{\gamma}$ ，那么紧跟在 $\alpha$ 之后的 $\beta$ 是句柄。

最右句型：所有在最右推导中出现的句型，其内句柄右边的串 $w$ 只包含终结符号。

将 $\beta$ 替换为 $A$ （规约）之后得到的串（ $\alpha A w$ ）是 $\gamma$ 的某个 最右推导序列 中出现在位于 $\gamma$ （ $\alpha \beta w$ ）之前的最右句型。

句柄可能存在多个，如果一个文法是 无二义性 的，那么该文法的 每个最右句型都有且只有一个句柄。

句柄的寻找方法

给定：

S = \gamma_0 \stackrel{rm}{\Rightarrow} \gamma_1 \stackrel{rm}{\Rightarrow} \gamma_2 \stackrel{rm}{\Rightarrow} \cdots \stackrel{rm}{\Rightarrow} \gamma_{n-1} \stackrel{rm}{\Rightarrow} \gamma_n = w

为了以相反顺序重构这个推导，我们在 $\gamma_n$ 中寻找句柄 $\beta_n$ ，并将 $\beta_n$ 替换为相关产生式 $A \rightarrow \beta_n$ 的头部 $A$ ，得到前一个最右句型 $\gamma_{n-1}$ 。

移入 - 归约语法分析技术

移入 - 归约语法分析是一种 自底向上 的语法分析技术，主要操作包括移入和归约。

组成

栈：存放已识别的文法符号，句柄通常出现在栈的顶部
输入缓冲区：存放待分析的符号，通常显示在右侧

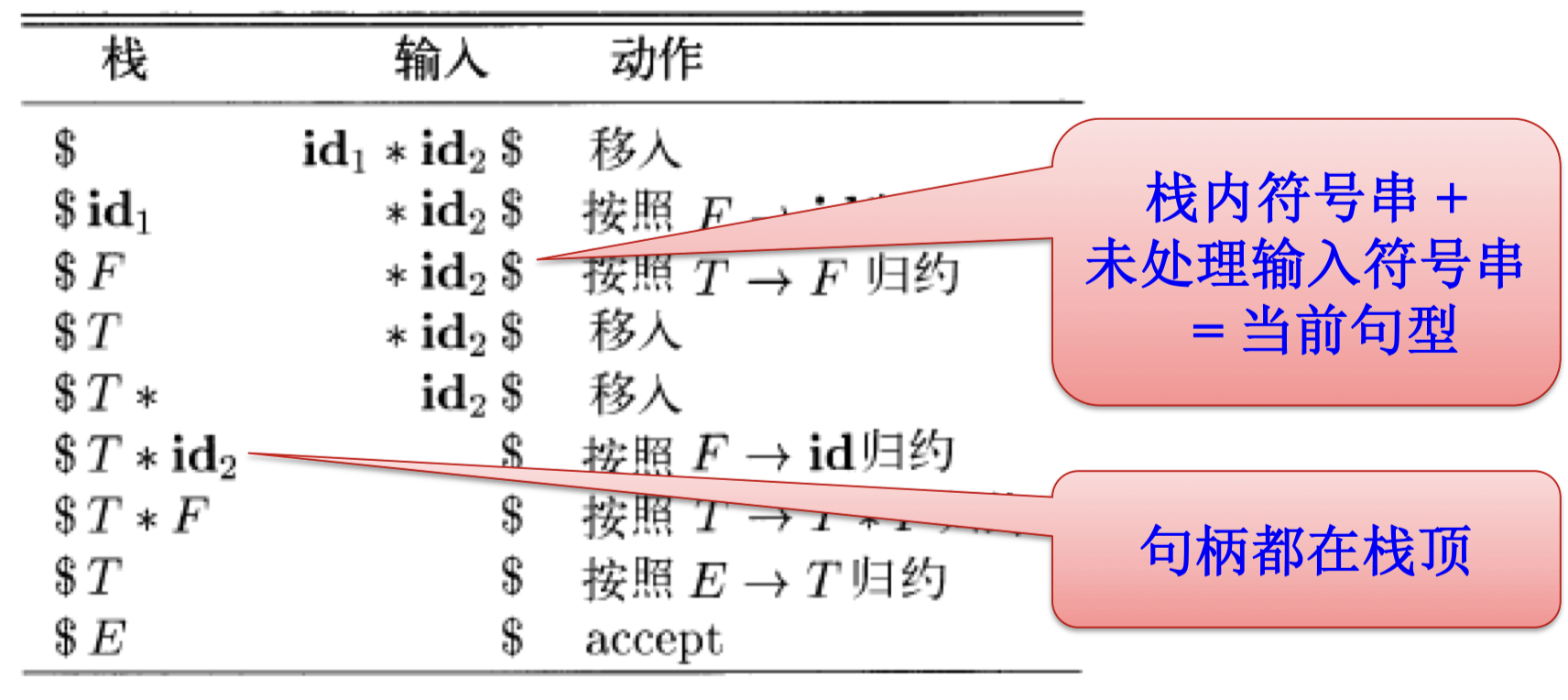
主要操作

移入（shift）：将下一个输入符号移到栈的顶部
归约（reduce）：将栈顶符号串（右部）替换为相应的产生式左部
接受（accept）：语法分析成功完成
报错（error）：发现语法错误，并调用错误恢复工具

LR ( $k$ ) 中的 $k$ 表示 在输入中向前看 $k$ 个符号。

移入 - 归约的语法分析技术可以使用栈中离栈顶很远的信息（向前看符号）来引导语法分析过程。

移入 - 归约语法分析中的冲突

有些上下文无关文法不能使用移入 - 归约语法分析技术。

即使知道了栈中的所有内容以及接下来的 $k$ 个输入符号，我们仍然可能会遇到：

移入 / 归约冲突：无法判断应该进行移入还是归约操作
归约 / 归约冲突：无法在多个可能的归约方法中选择正确的归约动作

接下来，我们举例说明。

移入 / 规约冲突举例

定义：在某个状态下，分析器既可以进行移入操作，也可以进行归约操作，但无法确定应该选择哪一种。

考虑以下文法：

$E \rightarrow E + E$
$E \rightarrow id$

假设当前状态是：

栈： $id$
剩余输入： $+ id$

在这种情况下，分析器可以选择：

移入：将 $+$ 移入栈中
归约：根据 $E \rightarrow id$ ，将 $id$ 归约为 $E$

这是一个典型的移入 / 归约冲突，因为分析器无法确定是应该移入 $+$ 还是进行归约。

规约 / 规约冲突举例

定义：在某个状态下，分析器可以进行多种归约操作，但无法确定应当选择哪一种。

考虑以下文法：

$S \rightarrow A$
$S \rightarrow B$
$A \rightarrow a$
$B \rightarrow a$

假设当前状态是：

栈： $a$
剩余输入：空

在这种情况下，分析器可以选择：

根据 $A \rightarrow a$ 进行归约。
根据 $B \rightarrow a$ 进行归约。

这是一个归约 / 归约冲突，因为分析器无法确定是应该将 $a$ 归约为 $A$ 还是 $B$ 。

LR ( $k$ ) 语法分析

LR ( $k$ ) 语法分析的定义：

L 表示对输入进行从左到右的扫描
R 表示反向构造出一个最右推导序列
$k$ 表示在做出语法分析决策时向前看 $k$ 个输入符号（用于指导规约操作）

对于实际应用， $k = 0$ 和 $k = 1$ 具有重要意义，因此这里只考虑 $k \leq 1$ 的情况。当省略 $k$ 时，假设 $k = 1$ 。

LR (0) 项和 LR (0) 自动机

LR (0) 项

项：一些状态，这些状态表示了语法分析过程中所处的位置。

一个文法 $G$ 的一个 LR (0) 项 是 $G$ 的一个产生式再加上一个位于它的右侧某处的点。

举例： $A \rightarrow XYZ$ ：

$A \rightarrow \cdot XYZ$
$A \rightarrow X \cdot YZ$
$A \rightarrow XY \cdot Z$
$A \rightarrow XYZ \cdot$

这里， $\cdot$ 标记了当前读到的位置， $\cdot$ 左边是已经读到的， $\cdot$ 右边是尚未读到的。

项表明了语法分析过程的给定点，我们已经看到一个产生式的哪些部分。

比如， $A \rightarrow X \cdot YZ$ 表明当前已经读到了 $X$ ，期望接下来在输入中看到一个从 $YZ$ 推导得到的串（从而可以规约回 $YZ$ ，再读入 $YZ$ 后即可规约回 $A$ ）。

LR (0) 项可分为四类：

移进项： $A \to \alpha \cdot a \beta, \quad a \in V_T$ ，表示当前可以读取符号 $a$ 并进行移入操作
待归约项： $A \to \alpha \cdot B \beta, \quad B \in V_N$ ，表示当前需要继续其他操作后（至少还要把 $B$ 给规约出来），才可以归约到 $A$
归约项： $A \to \alpha \cdot$ ，表示当前可以进行规约操作（已经把一个产生式体完全读入了），即将 $\alpha$ 规约为 $A$
接受项： $S' \to S \cdot$

对于产生式 $A \to \varepsilon$ 的唯一一项是 $A \to \cdot$ ，它是归约项。

项集：这些项的列表

我们还可以划分每个项为如下两类：

内核项：包括初始项 $S' \rightarrow \cdot S$ 以及点不在最左端的所有项（代表要么正在从头开始，要么已经有一些已读信息了）
非内核项：除了 $S' \rightarrow \cdot S$ 之外点在最左端的所有项（代表我们对于这个产生式完全没有任何已读信息）

规范 LR (0) 项集族的构造

为了构造一个文法的规范 LR (0) 项集族，我们定义了一个 增广文法 （augmented grammar）和两个函数：Closure 和 Goto。

增广文法

如果 $G$ 是一个以 $S$ 为开始符号的文法，那么 $G$ 的增广文法 $G'$ 就是在 $G$ 中加上新开始符号 $S'$ 和产生式 $S' \rightarrow S$ 而得到的文法。

当且仅当语法分析器要使用规则 $S' \rightarrow S$ 进行归约时（即 $S' \rightarrow S \cdot$ ），输入符号串被接受（即表明已经完全规约回到了原开始符号）。

引入这个新的开始产生式的目的是使得文法开始符号（ $S'$ ）仅出现在一个产生式的左边，从而使得分析器只有一个接受状态。

项集的闭包

如果 $I$ 是文法 $G$ 的一个项集，那么 $\text{Closure}(I)$ 就是根据下面的两个规则从 $I$ 构造得到的项集：

一开始，将 $I$ 中的各个项加入到 $\text{Closure}(I)$ 中
如果 $A \rightarrow \alpha \cdot B \beta$ 在 $\text{Closure}(I)$ 中， $B \rightarrow \gamma$ 是一个产生式，并且项 $B \rightarrow \cdot \gamma$ 不在 $\text{Closure}(I)$ 中，就将这个项加入其中。不断应用这个规则，直到没有新项可以加入到 $\text{Closure}(I)$ 为止

直观地讲， $\text{Closure}(I)$ 中的项 $A \rightarrow \alpha \cdot B \beta$ 表明在语法分析过程的某点上，我们认为接下来可能会在输入串中看到一个能够从 $B \beta$ 推导得到的子串。

这个可以从 $B \beta$ 推导得到的子串的某个前缀肯定可以从 $B$ 推导得到，而推导 / 逆向规约时必然要用某个 $B$ 产生式。

因此我们加入了各个 $B$ 产生式对应的项。也就是说，如果 $B \rightarrow \gamma$ 是一个产生式，那么我们把 $B \rightarrow \cdot \gamma$ 加入到 $\text{Closure}(I)$ 中。

Goto 函数

$\text{Goto}$ 函数形式为 $\text{Goto}(I, X)$ ，其中：

$I$ 是一个项集
$X$ 是一个文法符号

$\text{Goto}(I, X)$ 被定义为 $I$ 中所有形如 $[A \rightarrow \alpha \cdot X \beta]$ 的项所对应的项 $[A \rightarrow \alpha X \cdot \beta]$ 的集合的闭包，即：

$\text{Goto}(I, X) = \text{Closure}(\{ [A \rightarrow \alpha X \cdot \beta] \mid [A \rightarrow \alpha \cdot X \beta] \in I \})$

直观地讲， $\text{Goto}$ 函数用于定义一个文法的 LR (0) 自动机中的移入单个符号（ 终结符号或者非终结符号都可以 ）的步骤，也即一类 状态转换。

求 LR (0) 项集规范族的算法

\begin{aligned} &\text{void } items(G') \{ \\ &\quad C = \textbf{Closure}(\{[S' \to \cdot S]\}); \\ &\quad \text{repeat} \\ &\quad \quad \text{for (}C \text{ 中每个项集 } I \text{)} \\ &\quad \quad \quad \text{for (每个文法符号 } X \text{)} \\ &\quad \quad \quad \quad \text{if (} Goto(I, X) \text{ 非空且不在 } C \text{ 中)} \\ &\quad \quad \quad \quad \quad 将 Goto(I, X) 加入 C 中; \\ &\quad \text{until 在某一轮中没有新的项集被加入到 } C \text{ 中;} \\ &\} \end{aligned}

从初始项集开始，不断计算各种可能的后继，直到生成所有的项集。

LR (0) 自动机的构造

规范 LR (0) 项集族中的项集可以作为 LR (0) 自动机的状态
$\text{Goto}(I, X) = J$ ，则从 $I$ 到 $J$ 有一个标号为 $X$ 的转换
初始状态为 $\text{Closure}(\{ S' \rightarrow \cdot S \})$ 对应的项集
接受状态：包含形如 $A \rightarrow \alpha \cdot$ 的项集对应的状态，即任何表示识别出了一个句柄的状态都是这个自动机的终态
可以发现所有的终态都是规约动作，说明 LR 事实上就是一直规约句柄的过程
对于整个 LR (0) 的编译过程而言， $S'\to S \cdot$ 当然是表示编译完成的终态
但是 LR (0) 自动机只是我们构造 LR (0) 分析表的中间步骤
要手动填 Action 和 Goto 表之后才构成整个 LR (0) 分析流程

移入 - 归约决策过程：

假设文法符号串 $\gamma$ 使 LR (0) 自动机从开始状态运行到状态（项集） $j$ ：

归约判断：如果 $j$ $j$ 中有一个形如 $A \rightarrow \alpha \cdot$ $A \to α \cdot$ 的项，那么：
- 在 $\gamma$ 之后添加一些 终结符号 可以得到一个最右句型
- $\alpha$ 是 $\gamma$ 的后缀，且 $A \rightarrow \alpha$ 是这个句型的句柄
- 表示可能找到了当前最右句型的句柄
移入判断：如果 $j$ $j$ 中存在一个项 $B \rightarrow \alpha \cdot X \beta$ $B \to α \cdot Xβ$ ，那么：
- 在 $\gamma$ 之后 添加 $X \beta$ ，然后再添加一个终结符号串 可以得到一个最右句型
- 在这个句型中 $B \rightarrow \alpha X \beta$ 是句柄
- 此时表示还没有找到句柄，至少还需要移进 $X$

LR 语法分析表

语法分析表由两个部分组成：

一个语法分析动作函数 $\text{Action}$
一个转换函数 $\text{Goto}$

Action 表

$\text{Action}$ 函数有两个参数：

状态 $i$
终结符号 $a$ （或者是输入结束标记 $\$$ ）。

$\text{Action}[i, a]$ 的取值可以有下列四种形式：

移入（Goto） $S_j$ ： $j$ 表示一个状态， $S_j$ 表示移进（Shift）到 $j$ 。语法分析器的动作是将输入符号 $a$ 移入栈中，使用状态 $j$ 来代表 $a$
归约（Reduce） $r_j$ ：产生式 $j = A \rightarrow \beta$ ：语法分析器将栈顶的 $\beta$ 根据这个产生式归约为产生式头 $A$
接受（Accept）：语法分析器接受输入并完成语法分析过程
报错（Error）：语法分析器在输入中发现错误并执行某个纠正动作

Goto 表

我们把定义在项集上的 $\text{Goto}$ 函数扩展为定义在状态集上的函数：如果 $\text{Goto}[I_i, A]=I_j$ ，那么 $\text{Goto}$ 把状态 $i$ 和一个非终结符号 $A$ 映射到状态 $j$ 。

分析过程

把状态 0（ $S_0$ ）和符号 $\$$ 压入初始为空的栈里。
设置栈顶元素中的状态为 $s$ ，当前读入的符号为 $a$ 。
反复执行以下各动作，直到分析成功或发现语法错误为止：
1. 移进：若 $\text{Action}[s, a]=S_i$ ，（Shift，移进）则把 $a$ 和状态 $i$ 压进栈，读下一个输入符号到 $a$ 中
2. 归约：若 $\text{Action}[s, a]=r_j$ (reduce，即产生式 $j=A \rightarrow X_{m-k+1} X_{m-k+2} \cdots X_m$ )，则出栈 $k$ 项，把 $A$ 和 $s_{new}=\text{Goto}[s', A]$ 进栈，其中 $s'$ 是出栈 $k$ 项后新的栈顶元素中的状态
3. 接受：若 $\text{Action}[s, \$]=\text{accept}$ ，则分析成功，结束
出错：若 $\text{Action}[s, a]=\text{error}$ ，则转由错误处理程序

举例说明

文法：

\begin{aligned} E &\rightarrow T E' \\ E' &\rightarrow + T E' | \varepsilon \\ T &\rightarrow F T' \\ T' &\rightarrow * F T' | \varepsilon \\ F &\rightarrow ( E ) | id \end{aligned}

假设输入字符串为 $id + id * id$ 。

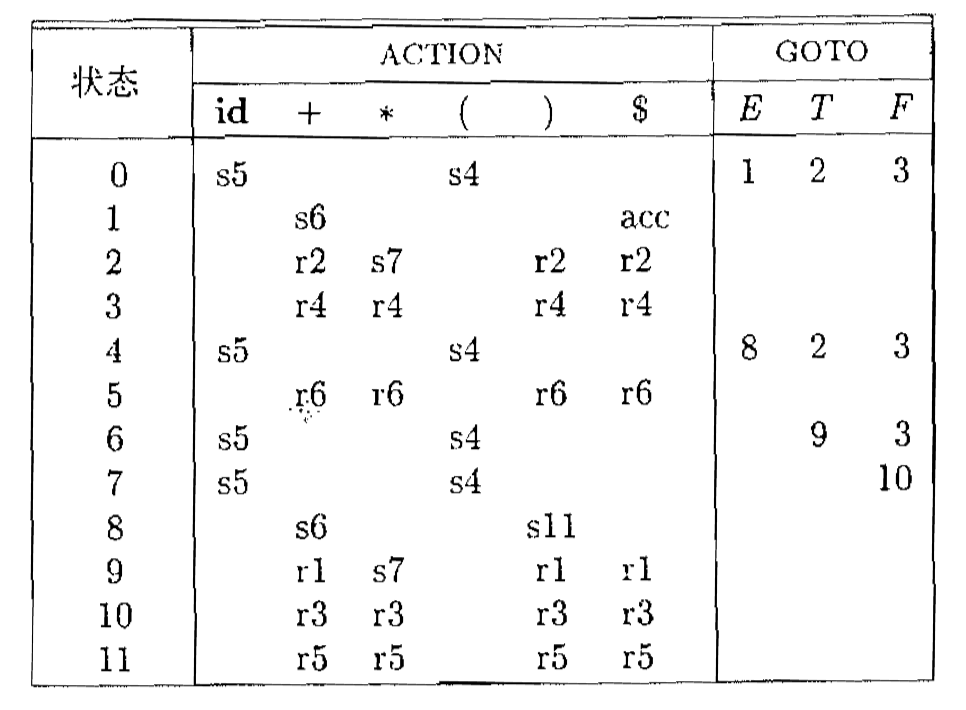
分析表结构

分析表的第一列是状态，第二列是 Action 部分，由 $|T|+1$ 列构成，第三列是 Goto 部分，由 $|V|$ 列构成。

\text{Action}[s, a] = \begin{cases} 移进 S_i & a\ 和状态\ i\ 进栈 \\ 归约 r_j & \text{出栈 k 项,然后}\ A\ \text{和 Goto[s',A] 进栈} \\ 接受 & \text{接受} \\ 出错 & \text{出错} \end{cases}

其中：

$s$ 是状态
$a$ 是读入的终结符（单词）或 $\$$
$k$ 是 $j$ 号产生式 $A \rightarrow \beta$ 的长度 $|\beta|$
$s'$ 是出栈 $k$ 项后新的栈顶元素中的状态

LR (0) 分析表中的冲突

移进规约冲突

假设有一个项集 $I$ 包含以下项目：

$A \rightarrow \alpha \cdot a \beta$
$B \rightarrow \gamma \cdot$

在这种情况下，如果当前输入符号是 $a$ ：

根据项目 $A \rightarrow \alpha \cdot a \beta$ ，分析器会尝试移进符号 $a$ ，以期待未来能够归约到 $A$
根据项目 $B \rightarrow \gamma \cdot$ ，分析器会尝试进行归约操作，把当前栈顶的 $\gamma$ 归约为 $B$

这就导致了移进 - 归约冲突。

移进规约冲突解决方案：SLR 分析表

SLR：Simple LR。

依据 $\text{Follow}$ 集来选择是否进行归约。

如果 $I=\{X \rightarrow \alpha \cdot b \beta$ ， $A \rightarrow \alpha \cdot$ ， $B \rightarrow \alpha \cdot\}$ ，且若 $\{b\}$ 、 $\text{Follow}(A)$ 、 $\text{Follow}(B)$ 两两不交，则面对应当前读入符号 $a$ ，状态 $I$ 的解决方法：

若 $a=b$ ，则移进
若 $a \in \text{Follow}(A)$ ，则用 $A \rightarrow \alpha$ 进行归约
若 $a \in \text{Follow}(B)$ ，则用 $B \rightarrow \alpha$ 进行归约
此外，报错

注：此处只举例了两个规约项、一个移入项，实际上可以有更多个规约项、移入项。

每个 SLR (1) 文法都是无二义性的，但是存在很多不是 SLR (1) 的无二义性文法。

SLR 原理：可行前缀（Viable Prefix）

不是所有的最右句型的前缀都可以出现在栈中，因为语法分析器在移入时 不能越过句柄。

可行前缀 (Viable Prefix)：某个最右句型的前缀，且没有越过该句型的句柄的右端。

有效项：如果存在 $S \Rightarrow \alpha Aw \Rightarrow \alpha \beta_1 \beta_2 w$ ，那么我们说项 $A \rightarrow \beta_1 \cdot \beta_2$ 对 $\alpha \beta_1$ 有效。

当我们知道 $A \rightarrow \beta_1 \cdot \beta_2$ 对 $\alpha \beta_1$ 有效：

如果 $\beta_2$ 不等于空，表示句柄尚未出现在栈中，应继续移进或者等待归约
如果 $\beta_2$ 等于空，表示句柄出现在栈中，应归约

如果某个时刻存在两个有效项要求执行不同的动作，那么就应该设法解决冲突。

冲突实际上表示可行前缀可能是两个最右句型的前缀，第一个包含了句柄，而另一个尚未包含句柄。

SLR 解决冲突的方法：假如要按照 $A \rightarrow \beta$ 进行归约，那么得到的新句型中 $A$ 后面跟着的是下一个输入符号。因此只有当下一个输入在 $\text{Follow}(A)$ 中时才可以归约。

如果在文法 $G$ 的 LR (0) 自动机中，从初始状态出发，沿着标号为 $\gamma$ 的路径到达一个状态，那么这个状态对应的项集就是 $\gamma$ 的 有效项集
回顾确定分析动作的方法，就可以知道我们实际上是按照有效项来确定的
为了避免冲突，归约时要求下一个输入符号在 $\text{Follow}(A)$ 中，且 SLR 语法保证了 $\text{Follow}$ 集合两两不交

SLR 语法分析器的弱点

没有展望符号

没有展望符号，不能确定规约之后还是不是可行前缀（即使 $\text{Follow}$ 集合得到满足也不保证）

举例：

假设此时栈中的符号串为 $\beta \alpha$ ，输入符号是 $a$
如果 $\beta A a$ 不能是某个最右句型的前缀，那么即使 $a$ 在某个句型中跟在 $A$ 之后，仍然不应该按照 $A \rightarrow \alpha$ 归约。

不能提前确定信息

$A \rightarrow \alpha \cdot$ 出现在项集中的条件：

首先 $A \rightarrow \cdot \alpha$ 出现在某个项集中，然后逐步读入 / 归约到 $\alpha$ 中的符号，点不断后移，直到末端
而 $A \rightarrow \cdot \alpha$ 出现的条件是 $B \rightarrow \beta \cdot A \gamma$ 出现在项中
期望首先按照 $A \rightarrow \cdot \alpha$ 归约，然后将 $B \rightarrow \beta \cdot A \gamma$ 中的点后移到 $A$ 之后
显然，在按照 $A \rightarrow \alpha$ 归约时要求下一个输入符号是 $\gamma$ 的第一个符号
但是从 LR (0) 项集中不能确定这个信息