本文主要介绍一些对于 ViT 的改进工作。
本文中，令牌 /token 为等价表述。
Image as Set of Points arxiv / 2303.01494
前情提要：CoAtNet 标准 ViT 因为使用了绝对位置 embedding，标准 ViT 缺少平移不变性（指只关注相对距离，不关注绝对位置）
CoAtNet 在自注意力之前先做卷积，可以有比原生 ViT 更好的表现。可以兼顾平移等变性（来自卷积）、输入自适应加权、全局感受野（来自自注意力）
核心改进：点集聚类 这篇文章提出了上下文聚类，它放弃了流行的卷积或注意力机制，而是新颖地考虑了经典算法 —— 聚类，来进行视觉学习的表示。
从图像到点集 首先将每个像素加上位置二维坐标信息 [ i w − 0.5 , j h − 0.5 ] \left[\frac{i}{w}-0.5, \frac{j}{h}-0.5\right] [ w i − 0.5 , h j − 0.5 ] P ∈ R 5 × n \mathbf{P}\in\mathbb{R}^{5\times n} P ∈ R 5 × n n = w × h n=w\times h n = w × h
对点集进行特征提取 使用聚类算法，在空间中均匀选择一些锚点，并将最近的 k k k
上下文聚类 ：将特征点 P ∈ R n × d \mathbf{P}\in\mathbb{R}^{n\times d} P ∈ R n × d P \mathbf{P} P P s \mathbf{P}_s P s S ∈ R c × n \mathbf{S}\in\mathbb{R}^{c\times n} S ∈ R c × n
特征聚合 ：基于与中心点的相似性动态聚合簇中的点，聚合特征 g g g
g = 1 C ( v c + ∑ i = 1 m s i g ( α s i + β ) ∗ v i ) , s . t . , C = 1 + ∑ i = 1 m s i g ( α s i + β ) g = \frac{1}{\mathcal{C}} \left( v_c + \sum_{i=1}^{m} \mathrm{sig}\left(\alpha s_i+\beta\right) * v_i \right), \qquad \mathrm{s.t.}, \ \ \mathcal{C} = 1+ \sum_{i=1}^{m}\mathrm{sig}\left(\alpha s_i+\beta\right) g = C 1 ( v c + i = 1 ∑ m sig ( α s i + β ) ∗ v i ) , s.t. , C = 1 + i = 1 ∑ m sig ( α s i + β ) 其中，α \alpha α β \beta β s i s_i s i m m m
特征分配 ：将聚合的特征 g g g
p i ′ = p i + F C ( s i g ( α s i + β ) ∗ g ) p_i' = p_i + \mathrm{FC}\left(\mathrm{sig}\left(\alpha s_i+\beta\right) * g\right) p i ′ = p i + FC ( sig ( α s i + β ) ∗ g ) arxiv / 2211.11167
前情提要：SSN 首先介绍一下什么 SSN 。
过往的 SLIC 算法基于 k − m e a n s k-means k − m e an s
其目标可以形式化表示为：给定图像 I ∈ R n × 5 I \in \mathbb{R}^{n \times 5} I ∈ R n × 5 n n n 5 5 5 X Y L a b XYLab X Y L ab m m m H ∈ { 0 , 1 , ⋯ , m − 1 } n × 1 H \in \{0,1,\cdots,m-1\}^{n \times 1} H ∈ { 0 , 1 , ⋯ , m − 1 } n × 1
那么 SLIC 的计算过程可以表示为：
将每个像素与五维空间中最近的超像素中心关联，即计算每个像素 p p p
H p t = arg min i ∈ { 0 , . . . , m − 1 } D ( I p , S i t − 1 ) H_p^t = \underset{i \in \{0,...,m-1\}}{\arg \min}D(I_p, S^{t-1}_i) H p t = i ∈ { 0 , ... , m − 1 } arg min D ( I p , S i t − 1 ) 其中， D D D D ( a , b ) = ∣ ∣ a − b ∣ ∣ 2 D(\textbf{a},\textbf{b}) = ||\textbf{a}-\textbf{b}||^2 D ( a , b ) = ∣∣ a − b ∣ ∣ 2
注意，此操作正是不可微分的来源 。
在每个超像素聚类内部平均像素特征（X Y L a b XYLab X Y L ab S t S^t S t S i S_i S i S i S_i S i
S i t = 1 Z i t ∑ p ∣ H p t = i I p S^t_i = \frac{1}{Z_i^t}\sum_{p | H_p^t = i} I_p S i t = Z i t 1 p ∣ H p t = i ∑ I p 其中 Z i t Z_i^t Z i t i i i
SLIC 在此基础上，将最近邻计算转为了可微分的操作，使用软关联 Q Q Q Q ∈ R n × m Q \in \mathbb{R}^{n \times m} Q ∈ R n × m H H H
Q p i t = e − D ( I p , S i t − 1 ) = e − ∣ ∣ I p − S i t − 1 ∣ ∣ 2 Q_{pi}^t = e^{-D(I_p,S_i^{t-1})} = e^{-||I_p - S_i^{t-1}||^2} Q p i t = e − D ( I p , S i t − 1 ) = e − ∣∣ I p − S i t − 1 ∣ ∣ 2 其中， Q p i t Q_{pi}^t Q p i t t t t p p p i i i I p I_p I p p p p S i t − 1 S_i^{t-1} S i t − 1 t − 1 t-1 t − 1 i i i
并且替换了超像素聚类中心的计算，改为计算像素特征的加权和：
S i t = 1 Z i t ∑ p = 1 n Q p i t I p S^t_i = \frac{1}{Z_i^t}\sum_{p=1}^n Q_{pi}^t I_p S i t = Z i t 1 p = 1 ∑ n Q p i t I p 其中，S i t S^t_i S i t t t t i i i Z i t = ∑ p Q p i t Z_i^t = \sum_p Q_{pi}^t Z i t = ∑ p Q p i t
同时，为了减少计算复杂度，对于每个像素，SSN 只对其原始位置划分得到的周围 3 × 3 = 9 3\times3=9 3 × 3 = 9
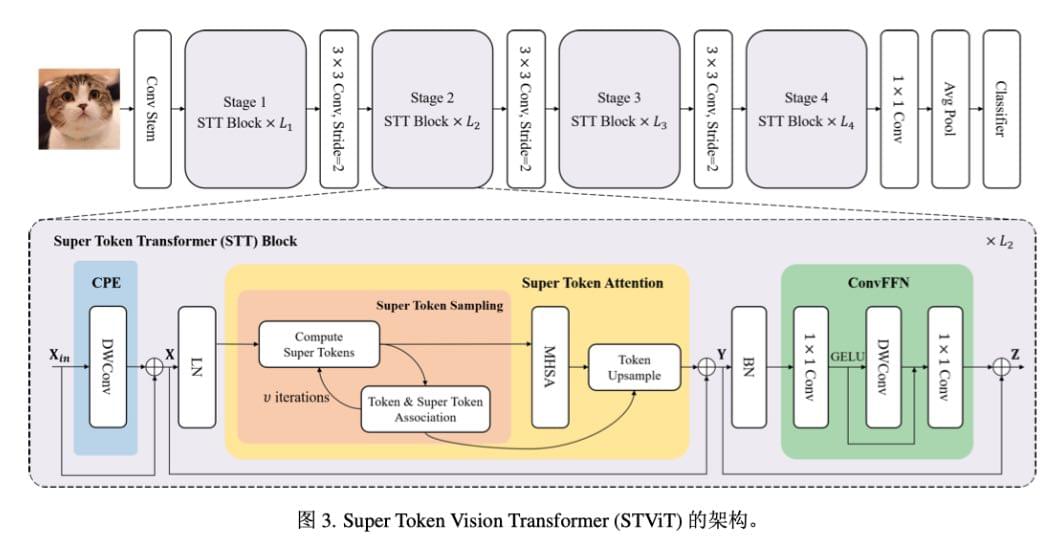
核心思想：将超像素的 SSN 应用到 token 上，实现 token 的聚合 STT 块整体过程可以表示为：
X = C P E ( X i n ) + X i n Y = S T A ( L N ( X ) ) + X Z = C o n v F F N ( B N ( Y ) ) + Y \begin{align} X &= {\rm CPE}(X_{in}) + X_{in} \\ Y &= {\rm STA}({\rm LN}(X)) + X \\ Z &= {\rm ConvFFN}({\rm BN}(Y)) + Y \end{align} X Y Z = CPE ( X in ) + X in = STA ( LN ( X )) + X = ConvFFN ( BN ( Y )) + Y CPE (Coordinate Pointwise Encoding, 坐标点注意力) 使用深度卷积的主要目的是减少计算量。
这一步和后面的的 ConvFFN 都是为了补充局部的细节。
STA (Super Token Attention, 超像素注意力) STS (Super Token Sampling, 超令牌采样) MHSA (Multi-Head Self-Attention, 多头自注意力) TU (Token Upsampling, 令牌上采样) 超令牌采样 超令牌采样基本上就是把 SSN 的思想应用到超令牌空间，对于先前嵌入得到的基础视觉令牌，我们进行如下操作：
初始化超令牌
给定视觉令牌 X ∈ R N × C X \in \mathbb{R}^{N \times C} X ∈ R N × C N = H × W N = H \times W N = H × W X i ∈ R 1 × C X_i \in \mathbb{R}^{1 \times C} X i ∈ R 1 × C m m m S ∈ R m × C S \in \mathbb{R}^{m \times C} S ∈ R m × C S 0 S^0 S 0 h × w h \times w h × w m = H h × W w m = \frac{H}{h} \times \frac{W}{w} m = h H × w W
将令牌与超令牌关联
在第 t t t X X X S S S
Q t = Softmax ( X S t − 1 T d ) Q^t = \text{Softmax} \left(\frac{X {S^{t-1}}^{\text{T}}}{\sqrt{d}}\right) Q t = Softmax ( d X S t − 1 T ) 其中：
这个过程不同于 SSN 的原始设计，实际上是计算了令牌和超级令牌之间的点积相似度，而不是 SSN 的计算距离，并且使用了 Softmax 进行归一化，使得关联度具有概率解释。
（Q：这里其实我说不好那种方式更优，SSN 的话要求超令牌的欧几里得范数不是越大越相似，而是大概和令牌本身相似就好，但是超令牌采样这里，由于计算的是点积相似度，似乎是欧几里得范数越大越相似，后面归一化了那没事了）
更新超令牌
超令牌 S S S
S = ( Q ^ t ) T X S = ({\hat{Q}}^{t})^{\text{T}} X S = ( Q ^ t ) T X 其中， Q ^ t \hat{Q}^t Q ^ t Q t Q^t Q t
同样，为了减少计算量，这里也使用了和 SSN 类似的限制关联计算范围、减少更新次数的方法，来降低计算复杂度，并且仅在第一次迭代时更新超令牌。（Q：诶，那后面迭代了个啥）
通过加权和更新超令牌，我们使其更好地代表对应的视觉令牌。
超令牌自注意力机制 由于超令牌是视觉内容的紧凑表示，对其应用自注意力机制可以更关注全局上下文依赖关系，而不是局部特征。我们对采样得到的超令牌 S ∈ R m × C S \in \mathbb{R}^{m \times C} S ∈ R m × C
Attn ( S ) = Softmax ( q ( S ) k T ( S ) d ) v ( S ) = A ( S ) v ( S ) \text{Attn} (S) = \text{Softmax}\left(\frac{\mathbf{q}(S)\mathbf{k}^{\text{T}}(S)}{\sqrt{d}}\right) \mathbf{v}(S) = \mathbf{A}(S)\mathbf{v}(S) Attn ( S ) = Softmax ( d q ( S ) k T ( S ) ) v ( S ) = A ( S ) v ( S ) 其中：
A ( S ) = Softmax ( q ( S ) k T ( S ) d ) ∈ R m × m \mathbf{A}(S) = \text{Softmax}\left(\frac{\mathbf{q}(S)\mathbf{k}^{\text{T}}(S)}{\sqrt{d}}\right) \in \mathbb{R}^{m \times m} A ( S ) = Softmax ( d q ( S ) k T ( S ) ) ∈ R m × m q ( S ) = S W q \mathbf{q}(S) = SW_q q ( S ) = S W q k ( S ) = S W k \mathbf{k}(S) = SW_k k ( S ) = S W k v ( S ) = S W v \mathbf{v}(S) = SW_v v ( S ) = S W v W q W_q W q W k W_k W k W v W_v W v 令牌上采样 尽管超令牌能够通过自注意力机制捕获更好的全局表示，但它们在采样过程中丢失了大部分局部细节。
因此，我们并不直接将它们用作后续层的输入，而是将它们映射回视觉标记并添加到原始标记 X X X
T U ( A t t n ( S ) ) = Q A t t n ( S ) {\rm TU}({\rm Attn}(S)) = Q {\rm Attn}(S) TU ( Attn ( S )) = Q Attn ( S ) 其中：
Q ∈ R N × m Q \in \mathbb{R}^{N \times m} Q ∈ R N × m A t t n ( S ) ∈ R m × C {\rm Attn}(S) \in \mathbb{R}^{m \times C} Attn ( S ) ∈ R m × C FFN (Feed-Forward Network，前馈神经网络) 没啥说的，感觉也是补偿局部的细节学习能力。
MSViT: Dynamic Mixed-Scale Tokenization for Vision Transformers
Jakob Drachmann Havtorn, Amelie Royer, Tijmen Blankevoort, Babak Ehteshami Bejnordi
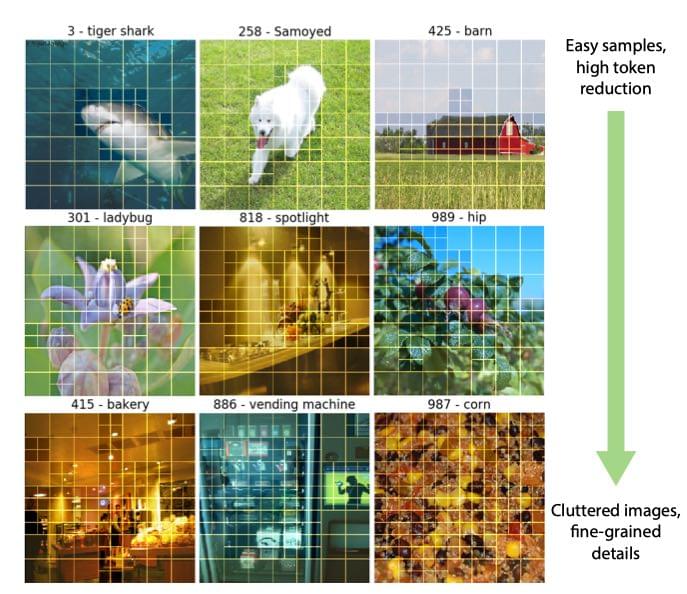
核心思想：依靠门控机制创建多尺度令牌 通过引入一个条件门控多层感知器 MLP，从而动态选择每个区域的令牌尺度，实现对于冗余令牌的抑制。
在这张图中，可以看到：
上面的图像元素较少，于是背景信息大多使用了较大的令牌尺度（粗令牌） 下面的图像元素很多，内容复杂且细节较多，于是大多使用了较小的令牌尺度（细令牌） 基础定义 我们首先定义细尺度和粗尺度，它们对应上图中两种 patch 尺度的取法：
S f S_{f} S f S c S_{c} S c 其中，S f < S c S_{f} < S_{c} S f < S c
提取方形 patch ：在两个尺度中提取方形 patch，总共有 N = N S f + N S c N = N_{S_{f}} + N_{S_{c}} N = N S f + N S c
门控机制的实现 门控机制：引入离散的门控机制 g g g
门控机制会解析每个粗尺度 token，并输出一个二元决策，即该区域是否应该在粗尺度或细尺度下进行 token 化。我们额外假定细尺度 S f S_{f} S f S c S_{c} S c i i i i i i C ( i ) = j C(i) = j C ( i ) = j
利用这个映射，在细 token 级别恢复完整的二元混合尺度掩码 m ‾ \overline{m} m
∀ j ∈ [ 1 , N S c ] , m j = GumbelSigmoid ( g ( x j ) ) ∈ [ 0 , 1 ] m ‾ j = STE ( m j ) ∈ { 0 , 1 } ∀ i ∈ [ N S c + 1 , N S c + N S f ] , m ‾ i = 1 − m ‾ C ( i ) \begin{align} \forall j \in [1, N_{S_{c}}],\ &m_j = \text{GumbelSigmoid}(g(x_j)) \in [0, 1] \\ &\overline{m}_j = \text{STE}(m_j) \in \{0, 1\} \\ \forall i \in [N_{S_{c}} + 1, N_{S_{c}} + N_{S_{f}} ],\ &\overline{m}_i = 1 - \overline{m}_{C(i)} \end{align} ∀ j ∈ [ 1 , N S c ] , ∀ i ∈ [ N S c + 1 , N S c + N S f ] , m j = GumbelSigmoid ( g ( x j )) ∈ [ 0 , 1 ] m j = STE ( m j ) ∈ { 0 , 1 } m i = 1 − m C ( i ) 其中：
m j m_j m j [ 0 , 1 ] [0, 1] [ 0 , 1 ] m ‾ j \overline{m}_j m j GumbelSigmoid \text{GumbelSigmoid} GumbelSigmoid STE \text{STE} STE 有关 Gumbel-Softmax：这是一个重参数化技巧，可以将从离散的概率分布采样这一不可导的操作，转化为一个可导的操作，从而允许进行反向传播。
重参数技巧可以理解为是把采样的步骤移出计算图，这样整个图就可以计算梯度反向传播更新了。其在 VAE 中广泛使用。
具体的数学证明，可以参见 Yiwei Zhang / 离散分布重参数化：Gumbel-Softmax Trick 和 Gumbel 分布
有关 STE：可以参见 刘泽春 / Straight-through estimator (STE) 解读
跨尺度参数共享 将不同尺度的 token 送入后续 ViT，一般需要引入额外参数或者其他方法，但是作者选择在这里直接将粗尺度的 token 通过线性插值调整到细尺度下的等效值，从而能够避免一些诸如路由不平衡和数据饥饿之类的问题。
Q：损失函数看不太懂，怎么学设计这种复杂损失函数啊？
Vision Transformers with Mixed-Resolution Tokenization
Tomer Ronen, Omer Levy, Avram Golbert
这篇文章的大致思想和 MSViT 一致，通过划分不同尺度的 patch 来减少输入 Transformer 的 token 数量，改进计算成本。
核心思想：划分不同尺度的 patch 动态选择 patch 尺度，通过一个评分函数（评分器） s c o r e score score
Input: Image i m ∈ R h × w × 3 , desired number of patches L ∈ N , patch edge sizes s m i n , s m a x ∈ N , saliency scorer s c o r e : p a t c h → R + Output: The set of chosen patches P c h o s e n Algorithm: P c h o s e n ← slice i m into a uniform grid with patch size s m a x while ∣ P c h o s e n ∣ < L do P s p l i t t a b l e ← { p ∣ p ∈ P c h o s e n & s i z e ( p ) ≥ 2 s m i n } p s p l i t ← arg max p ∈ P s p l i t t a b l e s c o r e ( p ) c h i l d r e n ( p s p l i t ) ← divide p s p l i t into 4 quadrants P c h o s e n ← c h i l d r e n ( p s p l i t ) ∪ P c h o s e n ∖ { p s p l i t } end Return P c h o s e n \begin{aligned} &\text{Input:} \\ &\quad\text{Image } im \in \mathbb{R}^{h \times w \times 3}, \\ &\quad\text{desired number of patches } L \in \mathbb{N}, \\ &\quad\text{patch edge sizes } s_{min}, s_{max} \in \mathbb{N}, \\ &\quad\text{saliency scorer } score : patch \rightarrow \mathbb{R}^{+} \\ &\text{Output:} \\ &\quad\text{The set of chosen patches } P_{chosen} \\ &\text{Algorithm:} \\ &\quad P_{chosen} \leftarrow \text{slice } im \text{ into a uniform grid with patch size } s_{max} \\ &\quad \text{while } |P_{chosen}| < L \text{ do} \\ &\quad\quad P_{splittable} \leftarrow \{p \mid p \in P_{chosen} \ \& \ size(p) \geq 2s_{min}\} \\ &\quad\quad p_{split} \leftarrow \arg\max_{p \in P_{splittable}} score(p) \\ &\quad\quad children(p_{split}) \leftarrow \text{divide } p_{split} \text{ into 4 quadrants} \\ &\quad\quad P_{chosen} \leftarrow children(p_{split}) \cup P_{chosen} \setminus \{p_{split}\} \\ &\quad \text{end} \\ &\text{Return } P_{chosen} \end{aligned} Input: Image im ∈ R h × w × 3 , desired number of patches L ∈ N , patch edge sizes s min , s ma x ∈ N , saliency scorer score : p a t c h → R + Output: The set of chosen patches P c h ose n Algorithm: P c h ose n ← slice im into a uniform grid with patch size s ma x while ∣ P c h ose n ∣ < L do P s pl i tt ab l e ← { p ∣ p ∈ P c h ose n & s i ze ( p ) ≥ 2 s min } p s pl i t ← arg p ∈ P s pl i tt ab l e max score ( p ) c hi l d re n ( p s pl i t ) ← divide p s pl i t into 4 quadrants P c h ose n ← c hi l d re n ( p s pl i t ) ∪ P c h ose n ∖ { p s pl i t } end Return P c h ose n 对于每个非 s m i n s_{min} s min s m i n s_{min} s min
位置嵌入：以由最小补丁大小 s m i n s_{min} s min ( x , y ) (x,y) ( x , y )
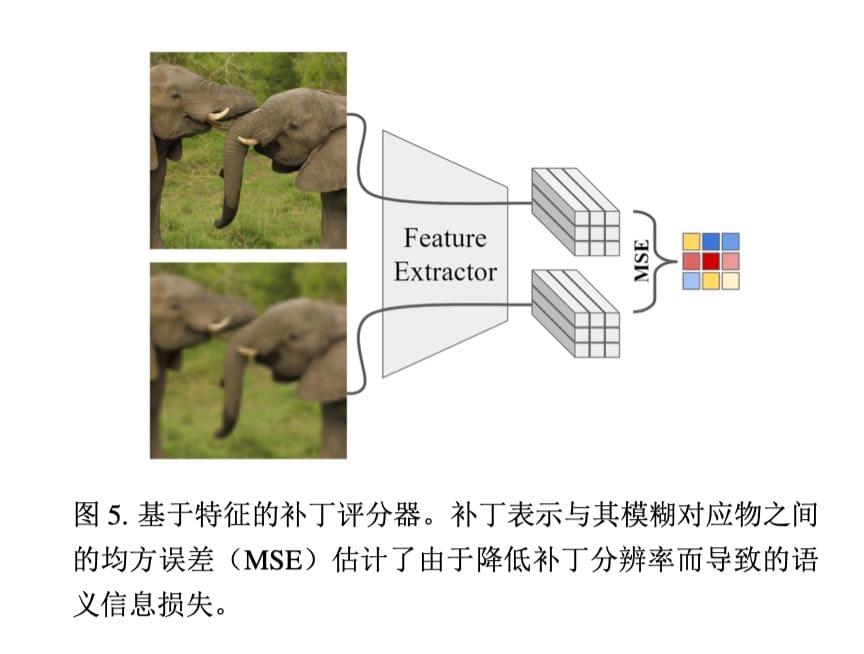
评分器：作者尝试了多种评分器，最终选择了基于特征的 patch 评分器：
Token Merging: Your ViT But Faster arxiv / 2210.09461
核心思想：令牌合并 本文提出了一种名为 “令牌合并” 的方法来组合令牌，而不是像过往文章中常见的修剪令牌操作。
新的 “令牌合并” 方法可以无需额外引入任何参数即可直接插入到现有的 ViT 中，直接进行对于相似的冗余令牌的合并，无需重新训练即可提高吞吐量。
核心方法 双重软匹配 两个令牌是否相似，定义为两个令牌在自注意力机制 QKV 中 Key 的点积相似度。因为 Key 总结了每个令牌中包含的信息，所以这种方法比直接使用令牌特征向量的欧氏距离要更好。
接下来，作者提出了一种名为 “双重软匹配” 的并行化、渐进性的匹配方法（注意这里不是聚类算法，因为聚类算法没有限制可以合并成一组的标记数量，而这对于网络是不好的，当太多的标记被合并为一组时，他们的相关度可能会下降，从而导致网络的性能随之下降）：
将标记划分为两个大小大致相等的集合 A \mathbb{A} A B \mathbb{B} B 从 A \mathbb{A} A B \mathbb{B} B 保留 r r r 合并仍然连接的标记（合并方法为平均它们的特征）。 将两个集合重新连接起来。 由于此方法创建的是一个二部图，其连通分量十分容易查找。并且对于同一集合内的令牌，不需要进行相似度的计算，从而提高了效率。
标记大小跟踪 由于进行了标记合并，现在每个标记和输入 patch 不再是一一对应，而这会影响 softmax 注意力的结果。
为此，一个很自然的想法是，对于 softmax 注意力机制进行加权，也即，合并次数较多、代表 patch 数量较多的令牌，我们给予其更高的权重。这就是 “比例注意力” 机制：
A = softmax ( Q K ⊤ d + log s ) A = \text{softmax}\left(\frac{QK^\top}{\sqrt{d}} + \log s\right) A = softmax ( d Q K ⊤ + log s ) 其中，s s s
可以理解为，原先是：
softmax ( z i ) = e z i ∑ j e z j \text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}} softmax ( z i ) = ∑ j e z j e z i 现在，对于其中某个 z i z_i z i s s s z i z_i z i z i + log s z_i + \log s z i + log s e e e s × e z i s \times e^{z_i} s × e z i s s s
这种方法确保了合并后的令牌依旧能够正确反映其所代表的多个输入 patch，从而保持了注意力机制的准确性。
