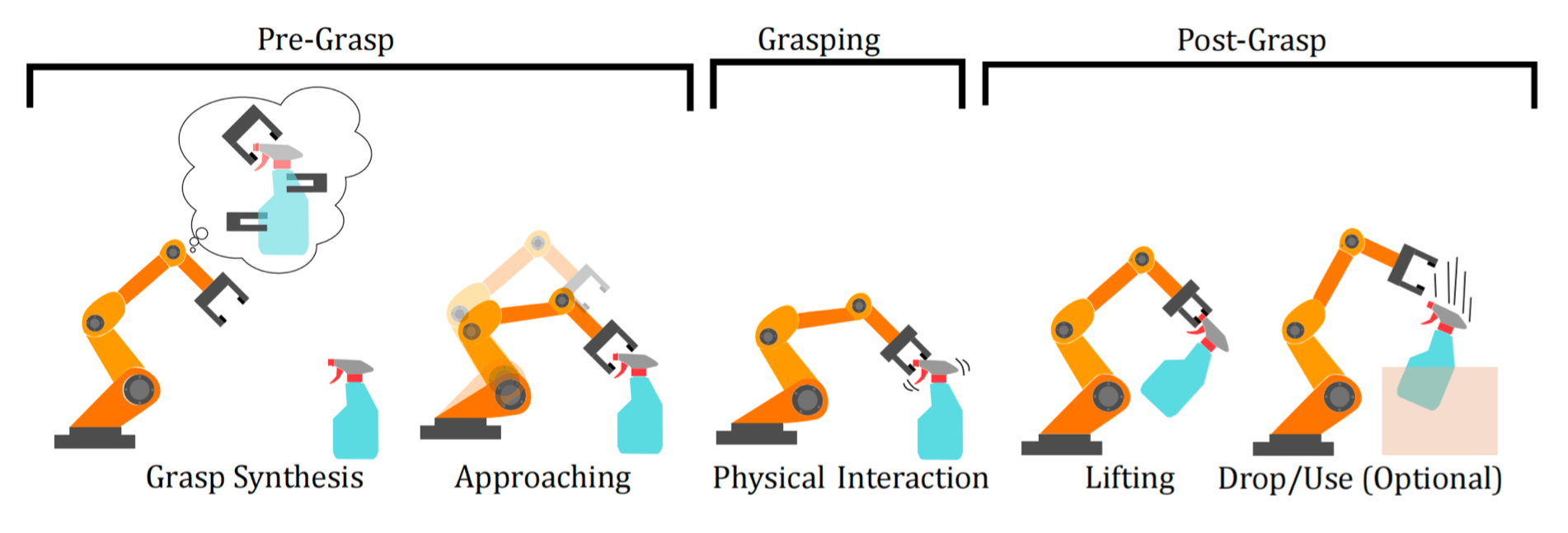
抓取(grasping) :通过末端执行器(end-effector)对物体施加约束(力和扭矩),以期望的方式限制物体运动的过程。
抓取合成(grasping synthesis) :对于夹爪位姿或者关节控制的高维搜索 / 优化问题。
抓握式操作 (Prehensile Manipulation):通过完全约束物体自由度实现精确控制非抓握式操作 (Non-prehensile Manipulation):利用推、滑等接触力学原理调整物体状态,适用于薄片状物体或预处理场景,不是所有动作都需要抓取
抓取的自由度#
抓取姿势(Grasp Pose) :手的位置、方向和关节状态
开环抓取与闭环抓取#
开环控制是指 不使用反馈机制 的控制系统。
控制命令直接发送给系统,不基于系统当前状态或结果进行调整
输入与输出之间没有信息回路
系统不会根据执行结果来自动修正控制信号
开环抓取 :基于视觉位姿估计,预测抓取位姿,执行抓取,视觉只会用到一次,如果失败(如掉落、没抓起来),不会尝试修正,“蒙着眼睛做事情”。
闭环抓取 :基于视觉位姿估计,预测抓取位姿,执行抓取,如果抓取失败,则调整抓取位姿,重新抓取。
开环抓取系统#
一般处理流程:
视觉感知
位姿估计
运动规划
控制执行
对已知物体的抓取#
由于物体信息已知,可以通过对物体的位姿进行预测。也就是在物体自身坐标系下进行抓取标注,然后转换到世界坐标系下。
RGB 图像,若满足
相机内参(将三维空间点投影到二维图像平面的关键参数,包括焦距、主点灯)已知:逆向的关键
物体大小已知:避免歧义(ambiguity)
道理我都懂,但是这个鸽子怎么这么大?
物体无对称性
那么其可以唯一对应一个位姿
点云(Point Cloud)图像,只需满足物体 无对称性 ,那么就可以唯一对应一个位姿。
Iterative Closest Point (ICP) 算法#
流程:
初始化变换估计 T 0 = ( R 0 , t 0 ) T_0 = (R_0, t_0) T 0 = ( R 0 , t 0 )
迭代直至收敛:
数据关联:确立变换后最近邻点对,建立模板点云 M M M S S S
C = { ( m i , s j ) ∣ s j = arg min s ∈ S ∥ T k m i − s ∥ } C = \{ (m_i, s_j) | s_j = \arg \min_{s \in S} \| T_k m_i - s \| \} C = {( m i , s j ) ∣ s j = arg s ∈ S min ∥ T k m i − s ∥ }
变换求解:最小化对应点距离
T k + 1 = arg min T ∑ ( m , s ) ∈ C ∥ T m − s ∥ 2 T_{k+1} = \arg \min_T \sum_{(m,s) \in C} \| Tm - s \|^2 T k + 1 = arg T min ( m , s ) ∈ C ∑ ∥ T m − s ∥ 2
问题:比较怕物体被挡住造成 点云缺失 。
对未知物体的抓取#
直接预测抓取位姿。
也有算法可以从见过同一类别物体进行泛化。
旋转回归(Rotation Regression)#
回归:估计连续变量。
旋转回归 :一种特殊的回归任务,对于输入信号,经由神经网络估计连续的旋转变量。
其中,表示方式空间 R R R X X X S O ( 3 ) \mathbb{SO}(3) SO ( 3 )
回顾一下 S O ( 3 ) \mathbb{SO}(3) SO ( 3 ) S O ( 3 ) \mathbb{SO}(3) SO ( 3 )
3D 旋转矩阵 R R R 3 × 3 3\times3 3 × 3
R ⊤ R = I R^{\top}R = I R ⊤ R = I det R = + 1 \det R = +1 det R = + 1
S O ( 2 ) / S O ( 3 ) \mathbb{SO}(2) / \mathbb{SO}(3) SO ( 2 ) / SO ( 3 )
与普通回归不同,旋转表示在非线性空间、非欧空间中,所以对于之前所讲过的所有旋转的表达方式,简单地使用 MSE 来作为监督信号都会不够理想。
这是因为,CNN 理应具有连续性,对于输入的微小变动,其输出不应当造成很大的改变。
而如果对于某一旋转表达方式,存在这种 Ground Truth 监督信号的跳变,神经网络为了拟合这种跳变点,就会导致其权重矩阵 W W W
所以,理想的表达方式,应当满足:
双射 ,表达方式到 S O ( 3 ) \mathbb{SO}(3) SO ( 3 ) 连续 , S O ( 3 ) \mathbb{SO}(3) SO ( 3 ) 奇点(Singularities)
欧拉角#
欧拉角使用三个角度(通常表示为 α \alpha α β \beta β γ \gamma γ
R = R x ( α ) R y ( β ) R z ( γ ) R = R_x(\alpha)R_y(\beta)R_z(\gamma) R = R x ( α ) R y ( β ) R z ( γ ) 问题 :欧拉角的表达方式天然存在非双射、万象节锁的问题
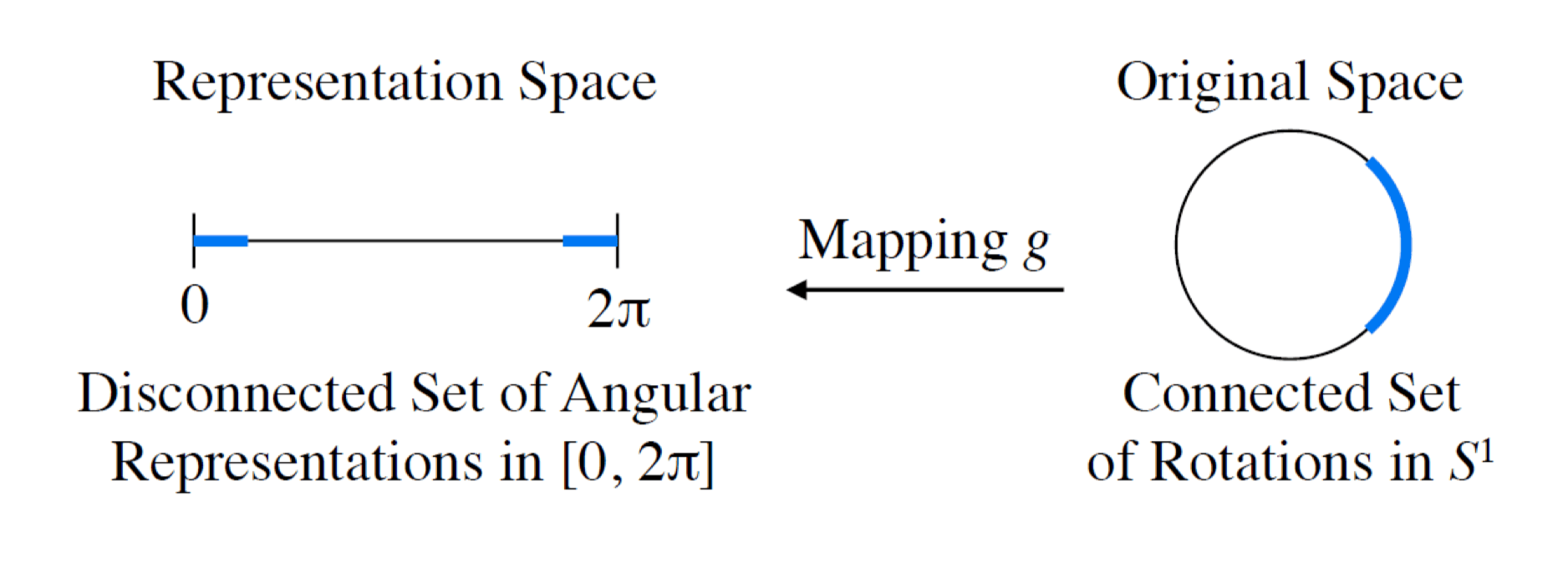
举例:考虑 2D 的情况,此时使用单一自由度 θ \theta θ
绕旋转轴转 0 0 0 2 π 2\pi 2 π S O ( 2 ) \mathbb{SO}(2) SO ( 2 )
一个解决方法是 引入冗余维度 ,把低维空间中的的不连续改成高维空间中的连续,如 θ → ( x , y ) \theta \to (x,y) θ → ( x , y )
轴角表示由一个单位向量 e = [ e x , e y , e z ] ⊤ \mathbf{e} = [e_x, e_y, e_z]^{\top} e = [ e x , e y , e z ] ⊤ θ \theta θ
( axis , angle ) = ( e , θ ) (\text{axis}, \text{angle}) = (\mathbf{e}, \theta) ( axis , angle ) = ( e , θ ) 可以使用罗德里格旋转公式(Rodrigues’ rotation formula)将轴角表示转换为旋转矩阵:
R = I + ( sin θ ) K + ( 1 − cos θ ) K 2 R = I + (\sin\theta)K + (1-\cos\theta)K^2 R = I + ( sin θ ) K + ( 1 − cos θ ) K 2 其中 K = [ e ] × K = [\mathbf{e}]_\times K = [ e ] ×
K = [ 0 − e z e y e z 0 − e x − e y e x 0 ] K = \begin{bmatrix}
0 & -e_z & e_y \\
e_z & 0 & -e_x \\
-e_y & e_x & 0
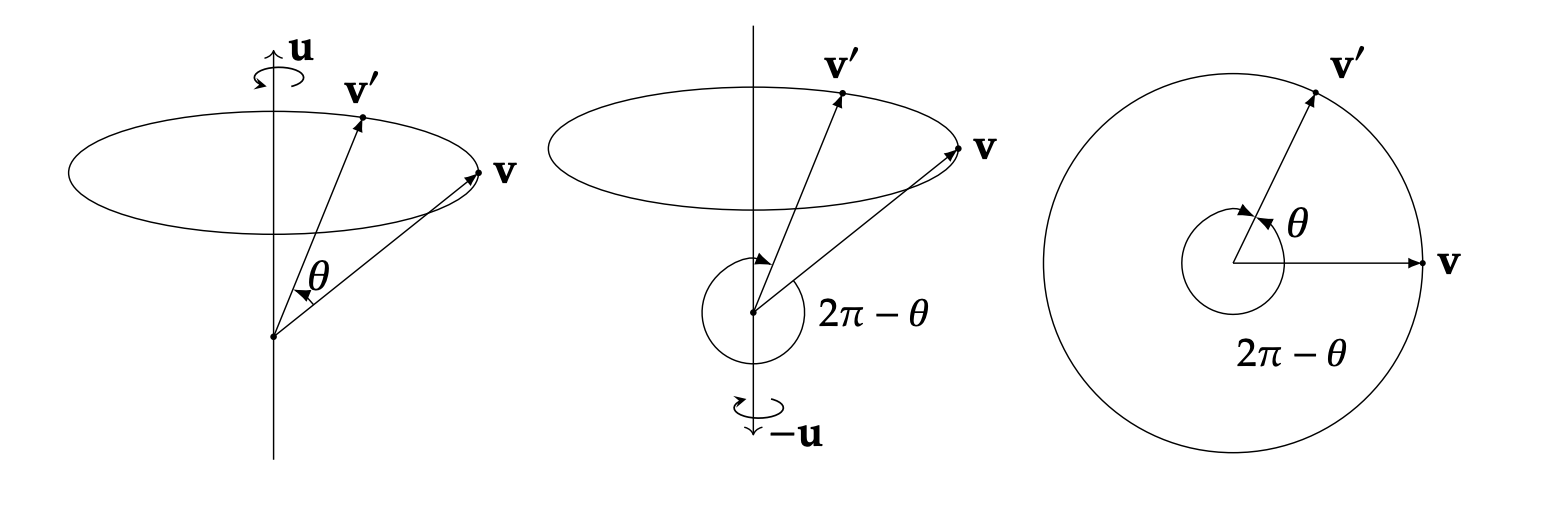
\end{bmatrix} K = 0 e z − e y − e z 0 e x e y − e x 0 问题: 当 θ = 0 \theta = 0 θ = 0 θ = π \theta = \pi θ = π ( e , π ) (\mathbf{e}, \pi) ( e , π ) ( − e , π ) (-\mathbf{e}, \pi) ( − e , π )
四元数#
四元数是复数的一种推广,形式为:
q = w + x i + y j + z k q = w + xi + yj + zk q = w + x i + y j + z k 其中 w w w v = ( x , y , z ) \mathbf{v} = (x, y, z) v = ( x , y , z ) i 2 = j 2 = k 2 = i j k = − 1 i^2 = j^2 = k^2 = ijk = -1 i 2 = j 2 = k 2 = ijk = − 1
任何一个旋转,即绕某个单位向量 ω ^ \hat{\omega} ω ^ θ \theta θ
q = [ cos θ 2 , sin θ 2 ω ^ ] q = \left[\cos\frac{\theta}{2}, \sin\frac{\theta}{2} \hat{\omega}\right] q = [ cos 2 θ , sin 2 θ ω ^ ] 问题 :四元数存在 “双重覆盖” 关系。
我们可以很容易地发现:
q = [ cos θ 2 , sin θ 2 ω ^ ] − q = [ − cos θ 2 , − sin θ 2 ω ^ ] = [ cos ( π − θ 2 ) , sin ( π − θ 2 ) ( − ω ^ ) ] \begin{aligned}
q &= \left[\cos\frac{\theta}{2}, \sin\frac{\theta}{2} \hat{\omega}\right] \\
-q &= \left[-\cos\frac{\theta}{2}, -\sin\frac{\theta}{2}\hat{\omega}\right] \\
&= \left[\cos(\pi - \frac{\theta}{2}), \sin(\pi - \frac{\theta}{2}) (-\hat{\omega})\right]
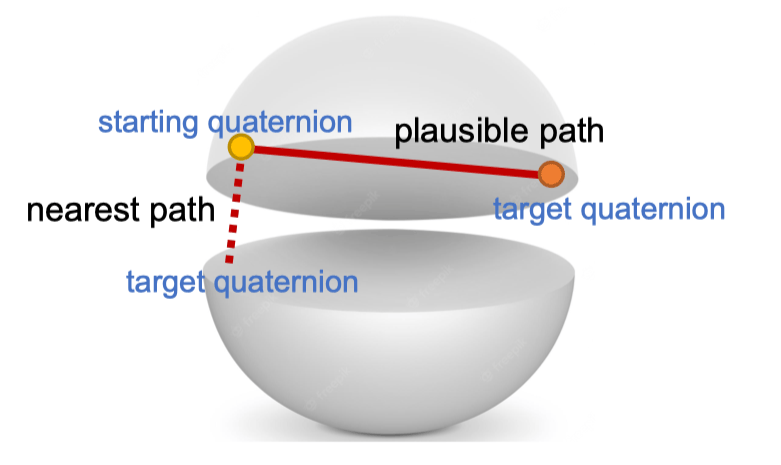
\end{aligned} q − q = [ cos 2 θ , sin 2 θ ω ^ ] = [ − cos 2 θ , − sin 2 θ ω ^ ] = [ cos ( π − 2 θ ) , sin ( π − 2 θ ) ( − ω ^ ) ] 是等价的(− q -q − q 2 π − θ 2\pi - \theta 2 π − θ
为此,我们通常约束四元数位于上半球(即 w ≥ 0 w \geq 0 w ≥ 0
临近球大圆的不连续性
球大圆上的不连续性:由于双重覆盖,我们只能取一个半圆,但是在这个切面圆的直径上,我们还是只能选取两个切点中的一个(否则又存在双重覆盖问题,q = − q q = -q q = − q
6D 表示#
为了解决不连续性问题,我们放弃了选择上述方法,改为回到旋转矩阵本身。
直接尝试拟合旋转矩阵,会引入 9 个数的自由度,我们还需要映射到 S O ( 3 ) \mathbb{SO}(3) SO ( 3 )
第一列标准化
第二列只保留垂直于第一列的分量,然后标准化
第三列通过第一列和第二列的叉乘确定
形式化表示为:
f G S ( [ a 1 a 2 ] ) = [ b 1 b 2 b 3 ] f_{GS}\left(\begin{bmatrix} \mathbf{a}_1 & \mathbf{a}_2 \end{bmatrix}\right) = \begin{bmatrix} \mathbf{b}_1 & \mathbf{b}_2 & \mathbf{b}_3 \end{bmatrix} f GS ( [ a 1 a 2 ] ) = [ b 1 b 2 b 3 ] 其中:
b i = { N ( a 1 ) if i = 1 N ( a 2 − ( b 1 ⋅ a 2 ) b 1 ) if i = 2 b 1 × b 2 if i = 3 \mathbf{b}_i = \begin{cases}
N(\mathbf{a}_1) & \text{if } i = 1 \\
N(\mathbf{a}_2 - (\mathbf{b}_1 \cdot \mathbf{a}_2)\mathbf{b}_1) & \text{if } i = 2 \\
\mathbf{b}_1 \times \mathbf{b}_2 & \text{if } i = 3
\end{cases} b i = ⎩ ⎨ ⎧ N ( a 1 ) N ( a 2 − ( b 1 ⋅ a 2 ) b 1 ) b 1 × b 2 if i = 1 if i = 2 if i = 3 其中 N ( v ) N(\mathbf{v}) N ( v ) v \mathbf{v} v
这种表示实际上只有 6 个自由度,所以我们叫它 6D 表示方法。
然而,这个方法固然简单,但是他引入了新的问题:拟合得到的 9 个数彼此并不等价。
对于第一列,是一等公民,直接归一化
对于第二列,是二等公民,需要移除平行于第一列的分量
对于第三列,甚至完全不考虑它的数值,正交系的三个向量直接由前两个叉乘得到
所以,这种表示方式与传统的 L2 Norm 的损失函数并不协调。
当然我们可以相对应地分优先级,第一列直接算,第二列需要加权,第三列直接排除在损失函数之外,但直觉上就会感觉到不平衡的存在 —— 神经网络输出的各个神经元本应等价,但是你算 Loss 的时候还要排除,哪有这样的道理?
9D 表示#
9D 表示直接使用完整的旋转矩阵(9 个元素)作为表示。为将神经网络的欧几里得输出映射到 S O ( 3 ) \mathbb{SO}(3) SO ( 3 )
双射
连续
等价
我们使用奇异值分解(SVD)对之进行正交化:
R ^ = U [ 1 0 0 0 1 0 0 0 det ( U V ) ] V ⊤ \hat{R} = U\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & \det(UV)
\end{bmatrix}V^{\top} R ^ = U 1 0 0 0 1 0 0 0 det ( U V ) V ⊤ 其中 U U U V V V det ( U V ) \det(UV) det ( U V )
SVD 的基本过程
给定任意矩阵 M ∈ R 3 × 3 M \in \mathbb{R}^{3 \times 3} M ∈ R 3 × 3
M = U Σ V ⊤ M = U \Sigma V^{\top} M = U Σ V ⊤ 其中:
U U U V V V U U ⊤ = V V ⊤ = I U U^{\top} = V V^{\top} = I U U ⊤ = V V ⊤ = I Σ \Sigma Σ σ 1 ≥ σ 2 ≥ σ 3 ≥ 0 \sigma_1 \geq \sigma_2 \geq \sigma_3 \geq 0 σ 1 ≥ σ 2 ≥ σ 3 ≥ 0
对于我们预测的旋转矩阵而言,这里分解得到的奇异值会很接近 1,但不一定就是 1,所以直接换掉它来使之满足正交化条件。
优势 :CNN Friendly
不区分对待矩阵的每一行,实现完全连续、一一映射的表示
与神经网络的欧几里得输出空间兼容
增量旋转预测#
对于预测增量旋转(delta rotation),即 S O ( 3 ) \mathbb{SO}(3) SO ( 3 ) I I I
而且,此时由于四元数等表示方式需要预测参数更少,学习起来甚至可能更快。
Rotation Fitting#
使用神经网络先预测物体坐标或对应关系,然后解算旋转。具体步骤包括:
对物体表面的每个像素,预测其在物体建模模型上的 3D 坐标
基于这些对应关系拟合旋转矩阵
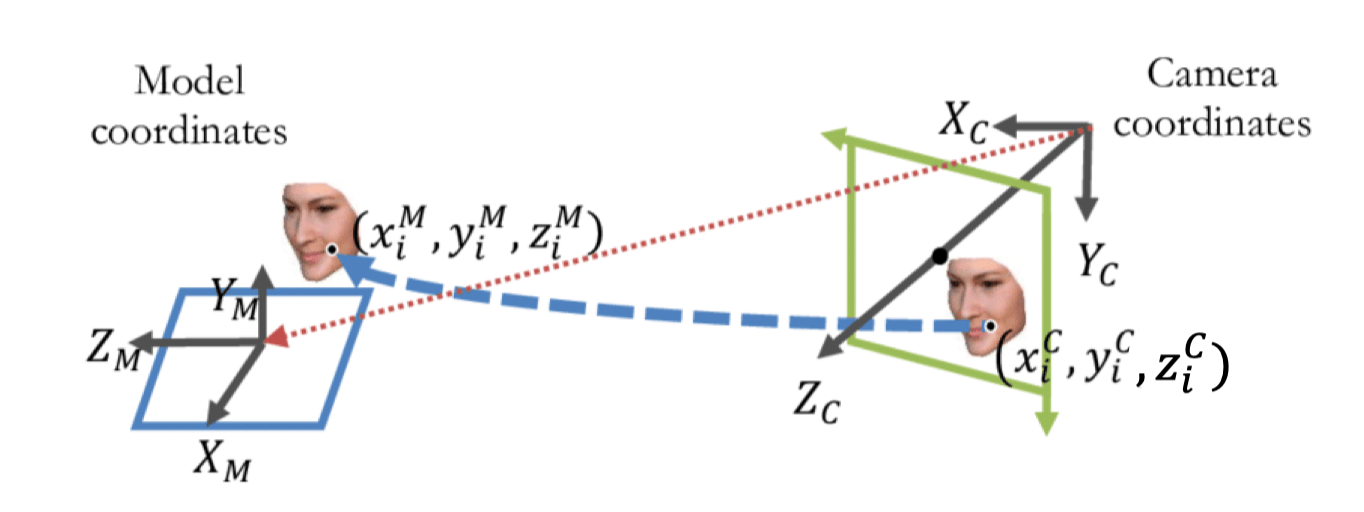
这种方法建立了模型坐标系(model) ( x i M , y i M , z i M ) (x_i^M, y_i^M, z_i^M) ( x i M , y i M , z i M ) ( x i C , y i C , z i C ) (x_i^C, y_i^C, z_i^C) ( x i C , y i C , z i C )
我们的目标是找到将模型坐标系转换到相机坐标系的最优变换矩阵(要求物体大小不变)。
这要求物体是见过的、标注过的,不然没法比对(缺乏 ( x i M , y i M , z i M ) (x_i^M, y_i^M, z_i^M) ( x i M , y i M , z i M )
有 Depth 信息:3d to 3d,( u , v , d ) → ( x i M , y i M , z i M ) (u,v, d) \to (x_i^M, y_i^M, z_i^M) ( u , v , d ) → ( x i M , y i M , z i M )
没有 Depth 信息:2d to 3d,( u , v ) → ( x i M , y i M , z i M ) (u,v) \to (x_i^M, y_i^M, z_i^M) ( u , v ) → ( x i M , y i M , z i M )
正交 Procrustes 问题#
给定两组对应的 3D 点集,不考虑位移 t t t
定义:给定矩阵 M ∈ R n × p \mathbf{M} \in \mathbb{R}^{n \times p} M ∈ R n × p N ∈ R n × p \mathbf{N} \in \mathbb{R}^{n \times p} N ∈ R n × p
A ^ = arg min A ∈ R p × p ∥ M ⊤ − A N ⊤ ∥ F 2 = arg min A ∈ R p × p ∥ M − N A ⊤ ∥ F 2 subject to A ⊤ A = I \hat{\mathbf{A}} = \arg\min_{\mathbf{A} \in \mathbb{R}^{p \times p}} \|\mathbf{M}^{\top} - \mathbf{AN}^{\top}\|_F^2 = \arg\min_{\mathbf{A} \in \mathbb{R}^{p \times p}} \|\mathbf{M} - \mathbf{NA}^{\top}\|_F^2 \\
\text{subject to} \quad \mathbf{A}^{\top}\mathbf{A} = \mathbf{I} A ^ = arg A ∈ R p × p min ∥ M ⊤ − AN ⊤ ∥ F 2 = arg A ∈ R p × p min ∥ M − NA ⊤ ∥ F 2 subject to A ⊤ A = I 其中,∥ ⋅ ∥ F \|\cdot\|_F ∥ ⋅ ∥ F
∥ X ∥ F = trace ( X ⊤ X ) = ∑ i , j x i j 2 \|X\|_F = \sqrt{\text{trace}(X^{\top}X)} = \sqrt{\sum_{i,j} x_{ij}^2} ∥ X ∥ F = trace ( X ⊤ X ) = i , j ∑ x ij 2 这里:
M \mathbf{M} M
N \mathbf{N} N
求解的 A \mathbf{A} A N \mathbf{N} N M \mathbf{M} M
约束条件 A ⊤ A = I \mathbf{A}^{\top}\mathbf{A} = \mathbf{I} A ⊤ A = I A \mathbf{A} A
正交 Procrustes 问题有一个优雅的解析解,可以通过奇异值分解(SVD)获得。如果我们对矩阵 M ⊤ N \mathbf{M}^{\top}\mathbf{N} M ⊤ N
M ⊤ N = U D V ⊤ \mathbf{M}^{\top}\mathbf{N} = \mathbf{UDV}^{\top} M ⊤ N = UDV ⊤ 那么最优旋转矩阵为:
A ^ = U V ⊤ \hat{\mathbf{A}} = \mathbf{UV}^{\top} A ^ = UV ⊤ 数学证明#
首先回顾迹运算的性质:
线性性质:tr ( A + B ) = tr ( A ) + tr ( B ) \text{tr}(A + B) = \text{tr}(A) + \text{tr}(B) tr ( A + B ) = tr ( A ) + tr ( B )
循环性质:tr ( A B C ) = tr ( B C A ) = tr ( C A B ) \text{tr}(ABC) = \text{tr}(BCA) = \text{tr}(CAB) tr ( A BC ) = tr ( BC A ) = tr ( C A B )
转置性质:tr ( A ⊤ ) = tr ( A ) \text{tr}(A^{\top}) = \text{tr}(A) tr ( A ⊤ ) = tr ( A )
标量提取:tr ( c A ) = c ⋅ tr ( A ) \text{tr}(cA) = c·\text{tr}(A) tr ( c A ) = c ⋅ tr ( A ) c c c
与 Frobenius 范数的关系:∥ A ∥ F 2 = tr ( A ⊤ A ) = tr ( A A ⊤ ) \|A\|_F^2 = \text{tr}(A^{\top}A) = \text{tr}(AA^{\top}) ∥ A ∥ F 2 = tr ( A ⊤ A ) = tr ( A A ⊤ )
利用迹运算的性质和 A \mathbf{A} A A ⊤ A = I \mathbf{A}^{\top}\mathbf{A} = \mathbf{I} A ⊤ A = I
∥ M − N A ⊤ ∥ F 2 = tr ( ( M − N A ⊤ ) ⊤ ( M − N A ⊤ ) ) = tr ( M ⊤ M − M ⊤ N A ⊤ − A N ⊤ M + A N ⊤ N A ⊤ ) = tr ( M ⊤ M ) − tr ( M ⊤ N A ⊤ ) − tr ( A N ⊤ M ) + tr ( A N ⊤ N A ⊤ ) = tr ( M ⊤ M ) − tr ( M ⊤ N A ⊤ ) − tr ( ( M ⊤ N A ⊤ ) ⊤ ) + tr ( N ⊤ N A ⊤ A ) = tr ( M ⊤ M ) − 2 tr ( M ⊤ N A ⊤ ) + tr ( N ⊤ N ) \begin{aligned}
\|\mathbf{M} - \mathbf{NA}^{\top}\|_F^2
&= \text{tr}((\mathbf{M} - \mathbf{NA}^{\top})^{\top}(\mathbf{M} - \mathbf{NA}^{\top}))\\
&= \text{tr}(\mathbf{M}^{\top}\mathbf{M} - \mathbf{M}^{\top}\mathbf{NA}^{\top} - \mathbf{AN}^{\top}\mathbf{M} + \mathbf{AN}^{\top}\mathbf{NA}^{\top}) \\
&= \text{tr}(\mathbf{M}^{\top}\mathbf{M}) - \text{tr}(\mathbf{M}^{\top}\mathbf{NA}^{\top}) - \text{tr}(\mathbf{AN}^{\top}\mathbf{M}) + \text{tr}(\mathbf{AN}^{\top}\mathbf{NA}^{\top}) \\
&= \text{tr}(\mathbf{M}^{\top}\mathbf{M}) - \text{tr}(\mathbf{M}^{\top}\mathbf{NA}^{\top}) - \text{tr}((\mathbf{M}^{\top}\mathbf{NA}^{\top})^{\top}) + \text{tr}(\mathbf{N}^{\top}\mathbf{N}\mathbf{A}^{\top}\mathbf{A}) \\
&= \text{tr}(\mathbf{M}^{\top}\mathbf{M}) - 2\text{tr}(\mathbf{M}^{\top}\mathbf{NA}^{\top}) + \text{tr}(\mathbf{N}^{\top}\mathbf{N})
\end{aligned} ∥ M − NA ⊤ ∥ F 2 = tr (( M − NA ⊤ ) ⊤ ( M − NA ⊤ )) = tr ( M ⊤ M − M ⊤ NA ⊤ − AN ⊤ M + AN ⊤ NA ⊤ ) = tr ( M ⊤ M ) − tr ( M ⊤ NA ⊤ ) − tr ( AN ⊤ M ) + tr ( AN ⊤ NA ⊤ ) = tr ( M ⊤ M ) − tr ( M ⊤ NA ⊤ ) − tr (( M ⊤ NA ⊤ ) ⊤ ) + tr ( N ⊤ N A ⊤ A ) = tr ( M ⊤ M ) − 2 tr ( M ⊤ NA ⊤ ) + tr ( N ⊤ N ) 注意到第一项 tr ( M ⊤ M ) \text{tr}(\mathbf{M}^{\top}\mathbf{M}) tr ( M ⊤ M ) tr ( N ⊤ N ) \text{tr}(\mathbf{N}^{\top}\mathbf{N}) tr ( N ⊤ N ) A \mathbf{A} A tr ( M ⊤ N A ⊤ ) \text{tr}(\mathbf{M}^{\top}\mathbf{NA}^{\top}) tr ( M ⊤ NA ⊤ )
当我们有 SVD 分解 M ⊤ N = U D V ⊤ \mathbf{M}^{\top}\mathbf{N} = \mathbf{UDV}^{\top} M ⊤ N = UDV ⊤
tr ( M ⊤ N A ⊤ ) = tr ( U D V ⊤ A ⊤ ) = tr ( U D ( A V ) ⊤ ) = tr ( ( A V ) ⊤ U D ) ( 循环性质,左乘正交矩阵逆,右乘正交矩阵 ) = ∑ i = 1 d [ ( A V ) ⊤ U ] i i d i \begin{aligned}
\text{tr}(\mathbf{M}^{\top}\mathbf{NA}^{\top}) &= \text{tr}(\mathbf{UDV}^{\top}\mathbf{A}^{\top}) \\
&= \text{tr}(\mathbf{UD}(\mathbf{AV})^{\top}) \\
&= \text{tr}((\mathbf{AV})^{\top}\mathbf{UD}) \quad (\text{循环性质,左乘正交矩阵逆,右乘正交矩阵}) \\
&= \sum_{i=1}^{d}[(\mathbf{AV})^{\top}\mathbf{U}]_{ii}d_i
\end{aligned} tr ( M ⊤ NA ⊤ ) = tr ( UDV ⊤ A ⊤ ) = tr ( UD ( AV ) ⊤ ) = tr (( AV ) ⊤ UD ) ( 循环性质,左乘正交矩阵逆,右乘正交矩阵 ) = i = 1 ∑ d [( AV ) ⊤ U ] ii d i 其中 d i d_i d i D \mathbf{D} D i i i d d d M ⊤ N \mathbf{M}^{\top}\mathbf{N} M ⊤ N
为了最大化上述和式,我们需要使 ( A V ) ⊤ U (\mathbf{AV})^{\top}\mathbf{U} ( AV ) ⊤ U A V \mathbf{AV} AV U \mathbf{U} U ( A V ) ⊤ U (\mathbf{AV})^{\top}\mathbf{U} ( AV ) ⊤ U L 2 L_2 L 2
因此,该和式在所有 ( A V ) ⊤ U (\mathbf{AV})^{\top}\mathbf{U} ( AV ) ⊤ U
( A V ) ⊤ U = I A V = U A = U V ⊤ \begin{aligned}
(\mathbf{AV})^{\top}\mathbf{U} &= \mathbf{I} \\
\mathbf{AV} &= \mathbf{U} \\
\mathbf{A} &= \mathbf{UV}^{\top}
\end{aligned} ( AV ) ⊤ U AV A = I = U = UV ⊤ 后处理#
正交 Procrustes 问题的基本约束 A ⊤ A = I \mathbf{A}^{\top}\mathbf{A} = \mathbf{I} A ⊤ A = I A \mathbf{A} A det A = + 1 \det \mathbf{A} = +1 det A = + 1 反射 (改变手性,det A = − 1 \det \mathbf{A} = -1 det A = − 1
所以,如果计算出的 det ( U V ⊤ ) = − 1 \det(\mathbf{UV}^{\top}) = -1 det ( UV ⊤ ) = − 1 U V ⊤ \mathbf{UV}^{\top} UV ⊤ D \mathbf{D} D
A ^ = U ( 1 0 0 0 1 0 0 0 det ( U V ⊤ ) ) V ⊤ \hat{\mathbf{A}} = \mathbf{U}\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \det(\mathbf{UV}^{\top}) \end{pmatrix}\mathbf{V}^{\top} A ^ = U 1 0 0 0 1 0 0 0 det ( UV ⊤ ) V ⊤ 直观上,这代表选择翻转关联性最弱的方向,是因为这样做对整体对齐效果(即 Frobenius 范数或等价的迹最大化目标)的影响是最小的。
位移求解#
可以想到,一旦旋转矩阵确定,那么位移向量 t t t
将一个变换矩阵转换为刚才说的正交 Procrustes 问题,也只需要对两个原始点集 M \mathbf{M} M N \mathbf{N} N
步骤:
中心化
计算两个点集的质心:M ‾ \overline{\mathbf{M}} M N ‾ \overline{\mathbf{N}} N
得到中心化后的点集:M ~ = M − M ‾ \tilde{\mathbf{M}} = \mathbf{M} - \overline{\mathbf{M}} M ~ = M − M N ~ = N − N ‾ \tilde{\mathbf{N}} = \mathbf{N} - \overline{\mathbf{N}} N ~ = N − N
求解旋转 R ^ \hat{\mathbf{R}} R ^ M ~ \tilde{\mathbf{M}} M ~ N ~ \tilde{\mathbf{N}} N ~ 带约束的正交 Procrustes 算法 (要求 det ( R ) = + 1 \det(\mathbf{R})=+1 det ( R ) = + 1 R ^ \hat{\mathbf{R}} R ^ M ~ ⊤ ≈ R ^ N ~ ⊤ \tilde{\mathbf{M}}^{\top} \approx \hat{\mathbf{R}}\tilde{\mathbf{N}}^{\top} M ~ ⊤ ≈ R ^ N ~ ⊤
求解平移 T ^ \hat{\mathbf{T}} T ^ R ^ \hat{\mathbf{R}} R ^
T ^ = M ⊤ − R ^ N ⊤ ‾ \hat{\mathbf{T}} = \overline{\mathbf{M}^{\top} - \hat{\mathbf{R}} \mathbf{N}^{\top}} T ^ = M ⊤ − R ^ N ⊤
草,刚上完的计算机视觉导论还在追我!
对于 Outlier 较为敏感,使用 RANSAC 算法即可。
以下内容直接摘录自 CV 导论笔记,看过的可以直接跳。
最小二乘法(Least Square Method)#
定义:假设有一组数据点 ( x i , y i ) (x_i, y_i) ( x i , y i ) y = m x + b y = mx + b y = m x + b
其能量函数(损失函数)为:
E = ∑ i = 1 n ( y i − m x i − b ) 2 E = \sum_{i=1}^n (y_i - mx_i - b)^2 E = i = 1 ∑ n ( y i − m x i − b ) 2
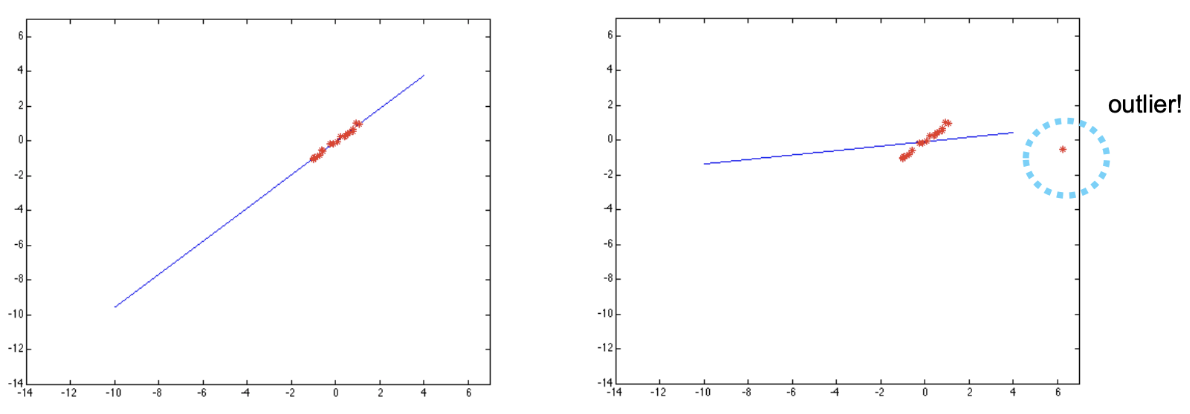
最小二乘法的一个问题是对细微噪声 鲁棒(robust) ,但是对于 离群点(Outliers) 敏感。如图,为了照顾一个离群点,整个直线发生了很大的旋转。
RANSAC(RANdom SAmple Consensus,随机抽样一致算法)#
动机 :我们想要一个自动化的算法,可以确定离群点(outliers)并排除之。
想法 :我们希望找到一条直线,使得这条直线有最多的内点(inliner)。
RANSAC loop :假设这条直线需要 2 个点(或选择 n n n
随机选择 k k k k × 2 k \times 2 k × 2
对每一组点计算出一条直线(使用 SVD)。
对每一组点的直线,计算所有点到这条直线的距离;若距离小于阈值,则认为该点是这条直线的内点(inliner)。
找到内点数量最多的直线,若数量超过阈值,则认为这条直线是最优的。
对最优直线,用其所有内点重新计算一次直线。
重复上述步骤,直到内点数量不再增加。
注意:此过程可推广到 n n n ≥ n \geq n ≥ n n − 1 n-1 n − 1
实际上,从今天的视角来看,此循环(loop)不再必需,因为我们可以并行地提出所有假设(Hypothesis),CV 导论中将此留作作业。
Instance level#
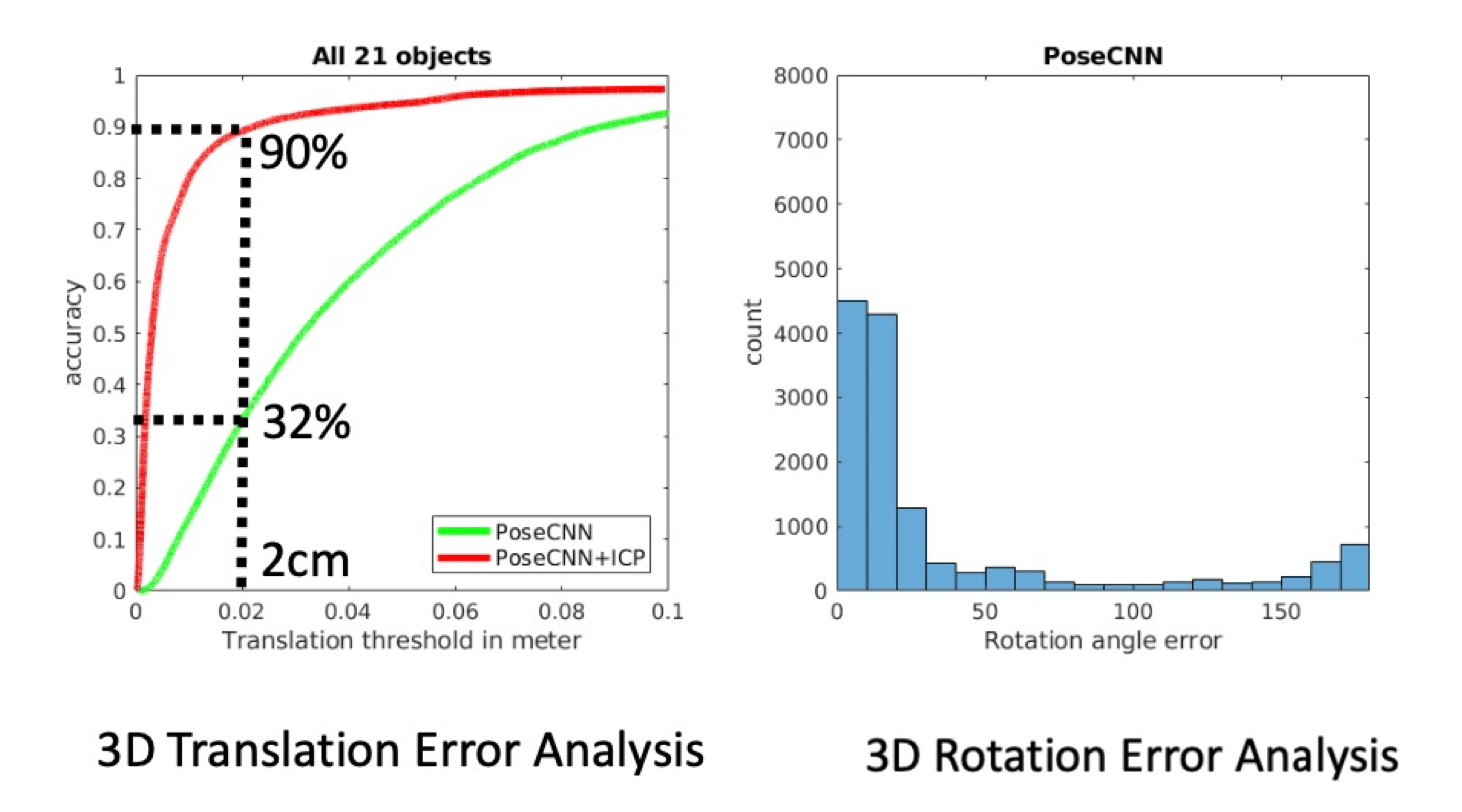
对物体级别的位姿变换预测,要求每个物体都已知(完整建模),典型算法如 PoseCNN,如果结合 ICP 算法可以在位移幅度较小的情况下更快的提升准确率(下节课详细讲)。
Catagory level#
对同一类别物体的位姿变换预测,这类物品通常具有共有结构,如茶杯具有相近的几何形状,可以用于定位(下节课详细讲)。
在同类别物体中进行泛化,但也因此受限,没见过的类别不行。
大小不知道,能给出旋转 Rotation 不能给平移 Translation,因为可能沿着物体光轴走,还是那个鸽子为什么这么大的问题,所以 Catagory level 必须要知道大小。
那么如何在同一类别物体的不同尺寸之间进行泛化呢,答案是类似归一化的想法,把同一类别的东西缩放到一个标准的 1x1x1 box 内,将其几何中心归一化到 box 中心,从而统一他们的尺度。