RL in VLA

iRe-VLA#

Paper ↗

Insight#

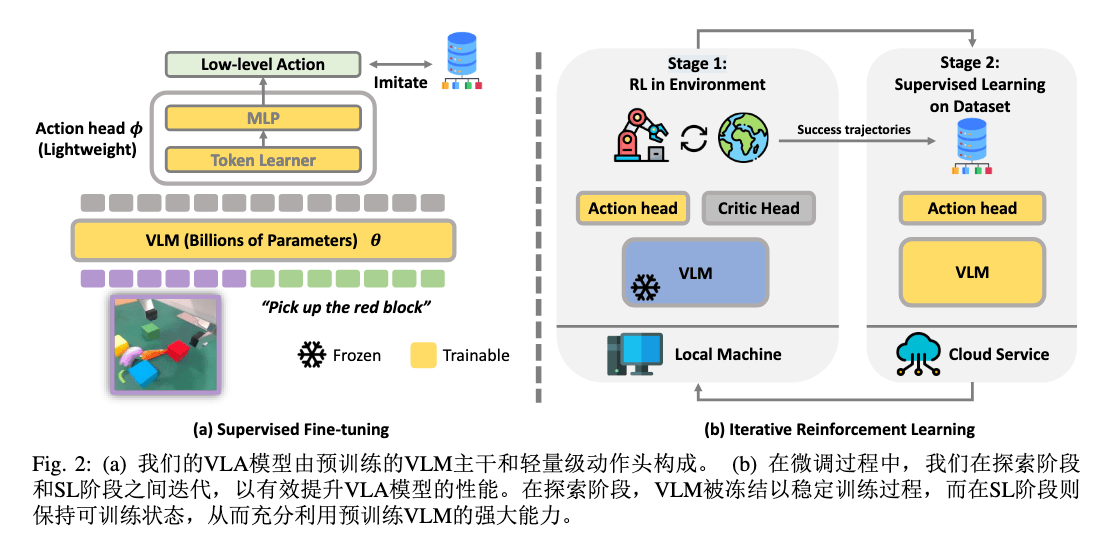
1. RL 只用以更新少部分参数，即 Action 头，从而避免 RL 大规模更新参数的不稳定。
2. SFT 来更新 LLM，更加稳定
3. 训练过程：先 SFT，然后迭代进行 RL（PPO，on-policy）和 SFT

Intresting#

1. LLM 用以高层规划（分解任务，无法直接应用于物理世界）或者低层控制信号（LLM 中引入 Action Token 或者后接动作头）
2. RL 直接用以提升 VLA 输出的低层控制信号
3. RL 得到的新成功轨迹加入数据集，on-policy
4. RL 用以探索，SFT 用以记忆

Arch#

Backbone：BLIP

Componentes：LoRA，TokenLearner（压缩多 token 到单 token）

Reward Signal：MSE (SFT), 01 Sparse (RL)

Result#

当在线数据 $|D_{\text{RL}}| > 0.3|D_e|$ 时，超越纯模仿学习的涌现能力（应对遮挡、动态干扰）。

RLPD#

Paper ↗

Efficient Online Reinforcement Learning with Offline Data

Insight#

1. 对称采样：50% 在线数据 + 50% 离线数据，去除对于离线数据质量的假设
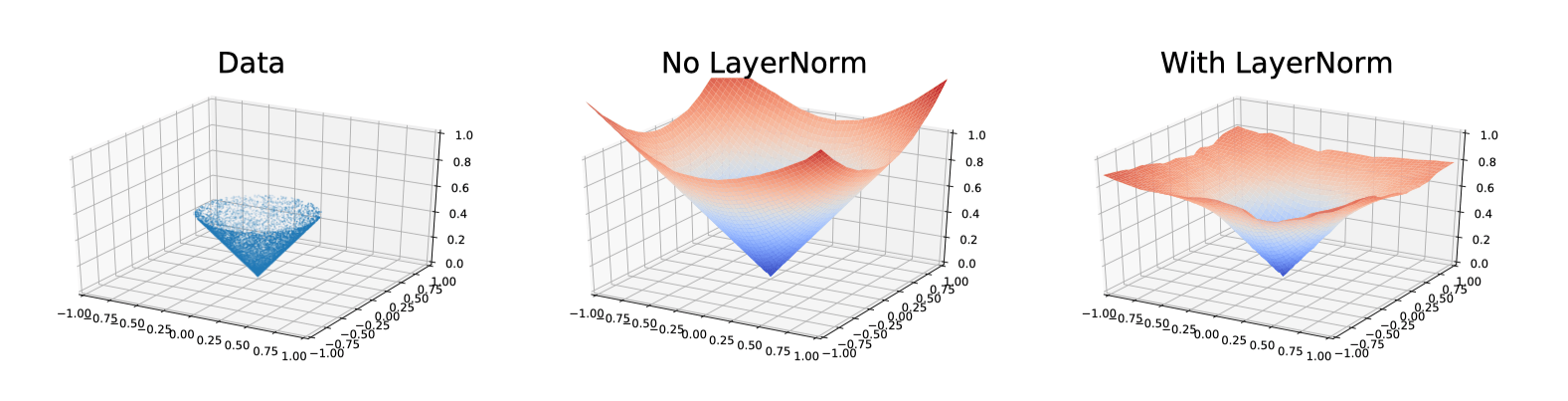
2. LayerNorm 约束价值函数 $Q$，抑制 OOD 时的过度自信（价值外推），稳定值函数
3. 高效采样：增加数据回放比 UTD，采用随机集成蒸馏（见下述算法）

Algorithm#

$$\begin{array}{l} \hline \textbf{算法} \ \text{在线强化学习结合离线数据 RLPD} \\ \hline \text{初始化:} \\ \quad \text{层归一化，集成规模 } E,\ \text{梯度步数 } G,\ \text{网络架构} \\ \quad \text{评论家参数 } \theta_1,...,\theta_E\ (\theta'_i \leftarrow \theta_i),\ \text{策略参数 } \phi \\ \quad \text{折扣因子 } \gamma,\ \text{温度系数 } \alpha,\ \text{EMA 权重 } \rho,\ \text{目标子集 } Z \in \{1,2\} \\ \quad \text{经验池 } \mathcal{R} = \varnothing,\ \text{离线数据集 } \mathcal{D} \\ \hline \text{主循环:} \\ \quad \text{获取初始状态 } s_0 \\ \quad \text{循环 } t=0 \text{ 至 } T: \\ \qquad \text{执行动作 } a_t \sim \pi_\phi(\cdot|s_t),\ \text{存储转移 } (s_t, a_t, r_t, s_{t+1}) \text{ 至 } \mathcal{R} \\ \hline \qquad \text{训练步骤 (重复 } G \text{ 次):} \\ \qquad\quad \text{采样 } b_R \leftarrow \frac{N}{2} \text{ 自 } \mathcal{R},\ b_D \leftarrow \frac{N}{2} \text{ 自 } \mathcal{D} \\ \qquad\quad \text{合并批次 } b = b_R \cup b_D \\ \qquad\quad \text{计算目标值:} \\ \qquad\qquad \mathcal{Z} \leftarrow \text{随机选取 } Z \text{ 个索引（从 } \{1,...,E\} \text{）} \\ \qquad\qquad y = r + \gamma \big[\min_{i\in\mathcal{Z}} Q_{\theta'_i}(s', \tilde{a}')\big] + \gamma\alpha \log \pi_\phi(\tilde{a}'|s') \\ \qquad\qquad \text{其中 } \tilde{a}' \sim \pi_\phi(\cdot|s') \\ \hline \qquad\quad \text{评论家更新:} \\ \qquad\qquad \text{循环 } i=1 \text{ 至 } E: \\ \qquad\qquad\quad \theta_i \leftarrow \arg\min \frac{1}{N}\sum (y - Q_{\theta_i}(s,a))^2 \\ \qquad\qquad \theta'_i \leftarrow \rho\theta'_i + (1-\rho)\theta_i \\ \hline \qquad\quad \text{策略更新:} \\ \qquad\qquad \phi \leftarrow \arg\max \frac{1}{E}\sum_{i=1}^E Q_{\theta_i}(s,\tilde{a}) - \alpha \log \pi_\phi(\tilde{a}|s) \\ \qquad\qquad \text{其中 } \tilde{a} \sim \pi_\phi(\cdot|s) \\ \hline \end{array}$$

Result#

收敛变快（300k vs 1M），效果提升。

HIL-SERL#

Paper ↗ / Homepage ↗ / Code ↗

Human in Loop SERL，双臂任务

Insight#

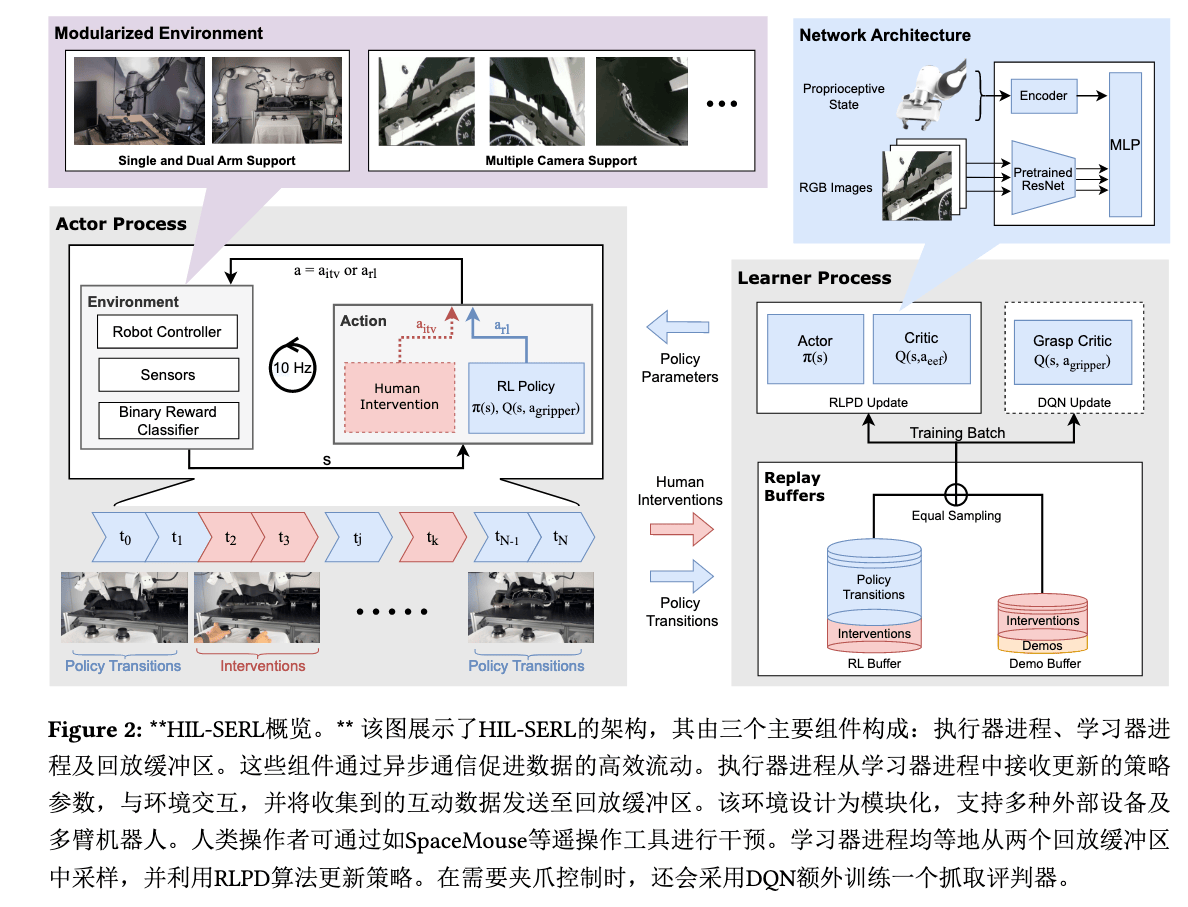
主动学习、人在回路：系统向模型请求可能的修正，offline 更新

Arch#

Backbone：ResNet-10

Reward：01 Sparse (MLP)

AC 架构：

• Actor：采样，送到 replay buffer，可以人为干预
• Learner：学习，RLPD 均等采样

两个缓冲区：

• 人类示范（离线）
• 策略实施（RL buffer）

对于人类产生的干预数据：

• actions 同时放到两个缓冲区（RL buffer + Demo buffer）
• P 概率转移只放到 RL buffer

单独用 DQN 学习抓握（夹爪建模为离散动作），输出动作基于 EEF 当前坐标系，抗干扰。

RLDG#

Paper ↗

Reinforcement Learning Distilled Generalist

Insight#

1. 使用 RL 生成高质量微调数据，微调 HIL-SERL
2. 数据质量 > 数据数量

ConRFT#

Paper ↗

Consistency-based Reinforced Fine-Tuning

Math#

离线 Critic 损失#

$$\mathcal{L}_{Q}^{offline}(\theta) = \alpha\left(\mathbb{E}_{s\sim\mathcal{D},a\sim\pi}[\max(Q_{\theta},V^{\mu})] - \mathbb{E}_{s,a\sim\mathcal{D}}[Q_{\theta}]\right) + \frac{1}{2}\mathbb{E}[(Q_{\theta}-\mathcal{B}^{\pi}\overline{Q})^2]$$

• $\max(Q_{\theta},V^{\mu})$：防止 OOD（分布外）动作的高估
• $\mathbb{E}[(Q_{\theta}-\mathcal{B}^{\pi}\overline{Q})^2]$：稳定 Q 值估计，防止离线数据不足导致的过拟合

一致性策略#

$$\pi_{\psi}(a|s) = f_{\psi}(a^k, k | E_{\phi}(s))$$

• $f_{\psi}$ 一致性策略是一个基于扩散模型的策略，负责去噪并生成最终动作。其目标是学习从单位高斯分布 $\mathcal{N}(0,I)$ 的随机噪声动作 $a^k$ 到专家动作分布 $a \sim \pi^*(a|s)$ 的映射。映射过程以当前状态编码 $E_{\phi}(s)$ 为条件。
• $a^k \sim \mathcal{N}(0, kI)$ 是第 $k$ 步的含噪声动作将扩散时间步 $[\epsilon, K]$ 划分为 $M$ 个子区间（边界为 $k_1=\epsilon \le \dots \le k_M=K$），每个子区间对应一个噪声尺度 $k_m$。例如，$\epsilon=0.002$ 表示初始噪声尺度极小，$K$ 为最大噪声尺度。

$$\mathcal{L}_{\pi}^{offline}(\psi) = -\eta\mathbb{E}[Q(s,a)] + \beta\mathbb{E}[d(f_{\psi}(a+k_mz),a)]$$

• $-\eta\mathbb{E}[Q(s,a)]$：引导策略朝高回报方向优化

• $\beta\mathbb{E}[d(f_{\psi}(a+k_mz),a)]$：迫使策略在不同噪声尺度下保持动作预测的一致性，也即约束动作与演示数据的一致，解决人类演示的次优问题

  对任意中间扩散步 $k_m$，若向专家动作 $a$ 添加噪声 $k_m z$ 得到扰动动作 $a + k_m z$，一致性策略 $f_{\psi}$ 应能将其映射回原始专家动作 $a$。

Insight#

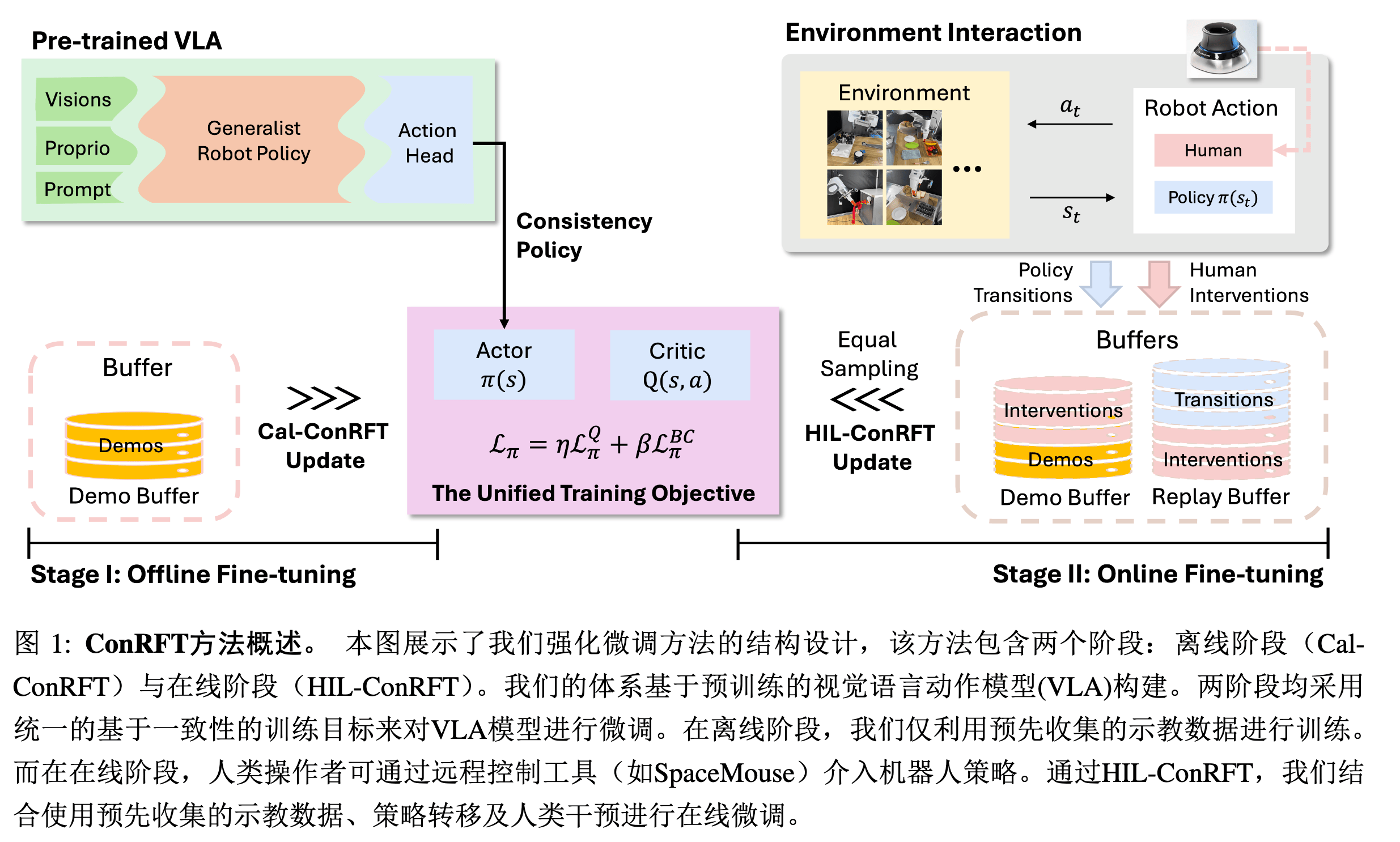
• 人在回路
• 一致性策略保证鲁棒性，但在线学习阶段逐步降低 $\beta$（BC 权重），实现从模仿到自主探索的平滑过渡
• 反馈信号中存在时间惩罚，引导快速完成任务

GRAPE#

Paper ↗

Generalizing Robot Policy via Preference Alignment

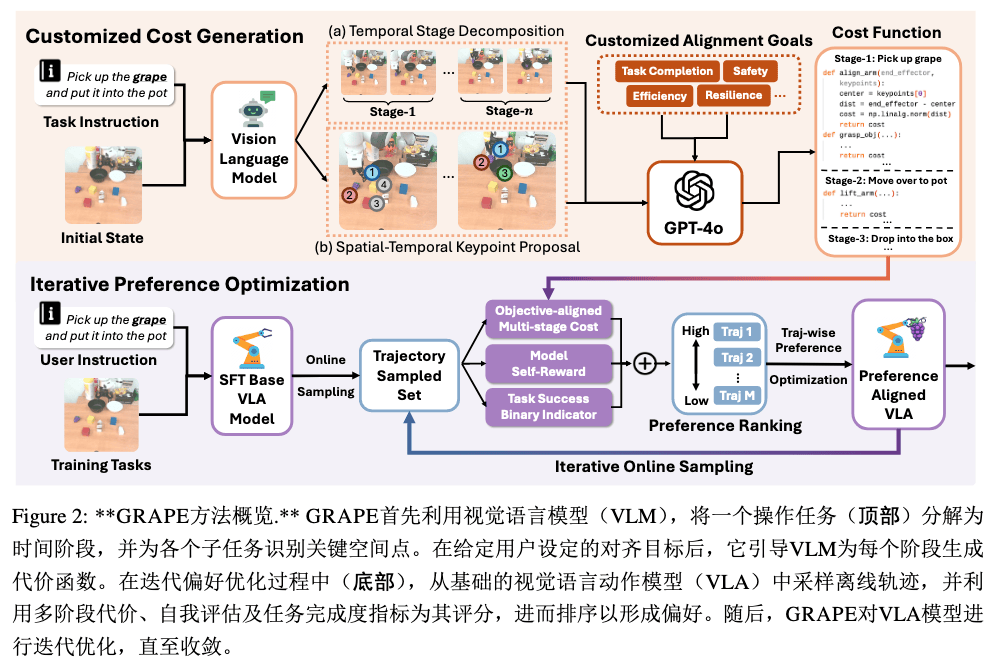
Math#

TPO 轨迹偏好优化损失（Trajectory-wise Preference Optimization Loss，类似 DPO）：

$$\mathcal{L}_{\text{TPO}} = -\mathbb{E} \left[ \log \sigma \left( \beta \left( \log \frac{\pi_\theta(\zeta_w)}{\pi_{\text{ref}}(\zeta_w)} - \log \frac{\pi_\theta(\zeta_l)}{\pi_{\text{ref}}(\zeta_l)} \right) \right) \right]$$

• $\beta$：温度系数，调节策略更新的强度（类比 “学习率”），越大这个 Loss 也越大，策略对比越强，更关注优选 / 劣选轨迹的差异；越小越保守更新，这项损失不重要。
• $\pi_\theta$：待优化的策略（参数为 $\theta$）
• $\pi_{\text{ref}}$：参考策略（预训练的初始策略）
• $\zeta_w, \zeta_l$：优选轨迹（winning）和劣选轨迹（losing）

Insight#

• 对比学习，增大优选轨迹概率比，降低劣选轨迹概率比

• 存在外部 Critic，由强大 LLM（GPT4o）给出，而非手动设计，某一时刻的成本为后续成本的乘积：

  $$R_{\text{ext}}(\zeta) = \prod_{i=1}^{\mathbf{S}} e^{-C^{S_i}(\{\kappa_{S_i}\})}$$

  其中：

  • $\mathbf{S}$：子系统的总数
  • $\{\kappa_{S_i}\}$：子任务 $S_i$ 的动态参数集合，如关节角度、速度、接触力等实时状态
  • $C^{S_i}$：子任务 $S_i$ 的成本函数，由 LLM 给出

• 完整的 Reward 同时包括外部 Critic、模型自身、以及成功与否信息加权，用以判断 $\zeta_w, \zeta_l$：

  $$R_{\text{GCPG}}(\zeta) = \lambda_1 R_\text{self}(\zeta) + \lambda_2 R_\text{ext}(\zeta) + \lambda_3 I_{\text{success}}(\zeta)$$

  其中：

  $$R_\text{self}(\zeta) =\log(\pi(\zeta, q)) = \log(\prod_{i=1}^T\pi(a_i \mid(o_i, q)))$$

Algorithm#

$$\begin{array}{l} \hline \textbf{算法} \ \text{迭代偏好优化算法} \\ \hline \text{初始化:} \\ \quad \text{基础 VLA 策略 } \pi_\theta,\ \text{任务指令集 } Q = \{q_i\},\ \text{阶段分解器 } \mathcal{M}_D \\ \quad \text{最大迭代次数 } K,\ \text{奖励权重 } \{\lambda_1, \lambda_2, \lambda_3\} \\ \quad \text{阶段关键点 } \{\kappa_{S_i}\},\ \text{成本函数 } \{C^{S_i}_j\}\ \text{及阈值 } \{\tau^{S_i}_j\} \\ \hline \text{主循环:} \\ \quad \text{循环 } k=1 \text{ 至 } K: \\ \qquad \text{用 } \pi_\theta \text{ 和 } Q \text{ 采样轨迹集 } \mathcal{D}^k = \{\zeta_i\}_{i=1}^M \\ \qquad \text{循环轨迹 } \zeta \in \mathcal{D}^k: \\ \qquad\quad \text{分解 } \zeta \text{ 为多阶段 } S\ \text{（阶段分解）} \\ \qquad\quad \text{计算各阶段成本 } C_{S_i}\ \text{（阶段成本）} \\ \qquad\quad \text{计算外部奖励 } R_{\text{ext}}(\zeta)\ \text{（全局成本）} \\ \qquad\quad \text{计算策略自奖励 } R_{\text{self}}(\zeta)\ \text{（轨迹自评估）} \\ \qquad\quad \text{验证任务成功指标 } I_{\text{success}}(\zeta)\ \text{（成功判别）} \\ \qquad\quad \text{聚合 GCPG 奖励 } R_{\text{GCPG}}(\zeta)\ \text{（综合奖励）} \\ \hline \qquad \text{按 } R_{\text{GCPG}}(\zeta) \text{ 排序 } \mathcal{D}^k \\ \qquad \text{从 top-}m \text{ 和 bottom-}m \text{轨迹生成配对 } \{\zeta_w, \zeta_l\} \\ \qquad \text{用 TPO 损失更新 } \pi_\theta\ \text{（偏好对齐）} \\ \hline \text{返回：优化策略 } \pi^* \\ \hline \end{array}$$

ASAP#

Paper ↗

Aligning Simulation and Real-World Physics

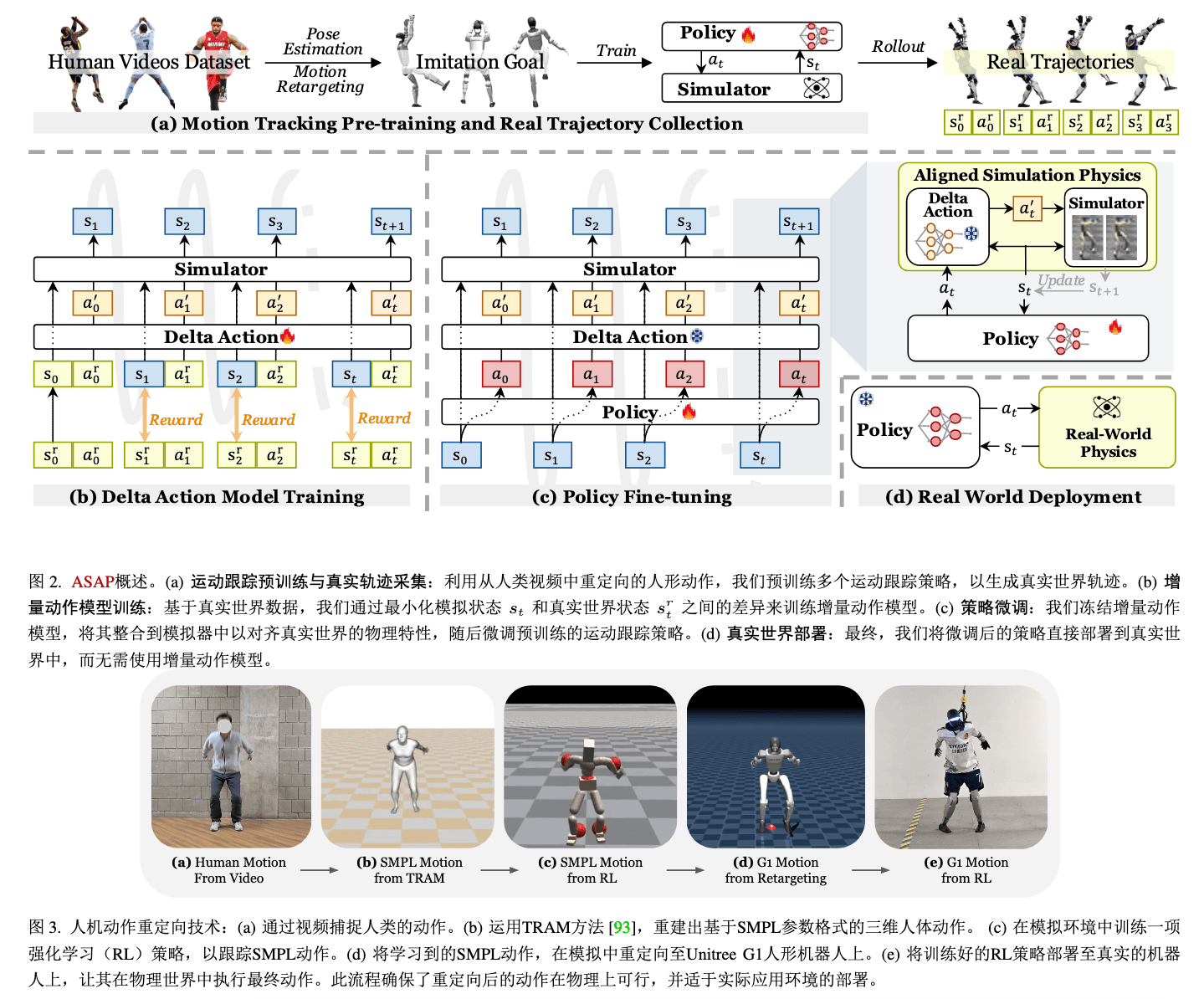
Insight#

1. 预训练得到基础策略（模拟环境中）

2. 后训练收集现实数据，模拟重放，获取跟踪误差，训练 delta 模型来补偿差异，形成残差校正项，通过动作空间修正隐式补偿，而不是像 SysID 一样显式建模物理参数来修正差异

   骑自行车时，人脑自动补偿重心偏移，而非计算力学方程

   $$s_{t+1} = f^{\text{ASAP}}(s_t, a_t) = f^\text{sim}(s_t, a_t + \pi^\Delta(s_t, a_t))$$

3. 非对称 AC 架构

   1. Actor 网络仅依赖本体感知输入（关节位置 / 速度、基座姿态、时间相位）
   2. Critic 网络额外访问特权信息（参考动作轨迹、全局位置）

Arch#

1. PPO，AC
2. Reward：$r_t = r_{\text{task}} + r_{\text{penalty}} + r_{\text{regularization}}$
   • 任务奖励（身体位置 / 旋转 / 速度匹配）
   • 惩罚项（关节极限、扭矩超限）
   • 正则化（动作平滑性）