构造抽象语法树的 SDD#
抽象语法树 (Abstract Syntax Tree)#
- 每个 结点 代表一个语法结构,对应于一个 运算符
- 结点的每个 子结点 代表其子结构,对应于 运算分量
- 表示这些子结构按照特定方式组成更大的结构
- 可以忽略掉一些标点符号等非本质的东西
语法树的表示方法#
- 每个结点用一个对象表示
- 对象有多个域
- 叶子结点中只存放词法值
- 内部结点中存放 op(操作符)值和参数(通常指向其它结点)
抽象语法树的例子#
产生式 S→if B then S1 else S2 的语法树#
if-then-else
/ | \
B S_1 S_2
plaintextclass StmtIfAST : public BaseAST {
public:
unique_ptr<BaseAST> exp;
unique_ptr<BaseAST> then_stmt;
optional<unique_ptr<BaseAST>> else_stmt;
Result print() const override;
};
cpp赋值语句的语法树#
assignment
/ \
variable expression
plaintextclass StmtAssignAST : public BaseAST {
public:
unique_ptr<BaseAST> l_val;
unique_ptr<BaseAST> exp;
Result print() const override;
};
cpp注意:在语法树中,运算符号和关键字都不在叶结点,而是在内部结点中出现。
抽象语法树 vs 具体语法树#
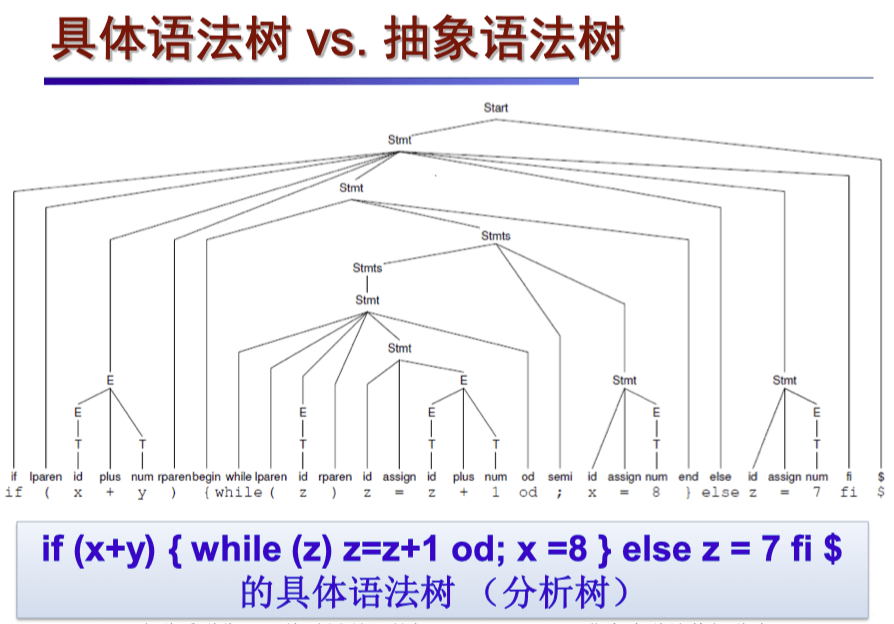
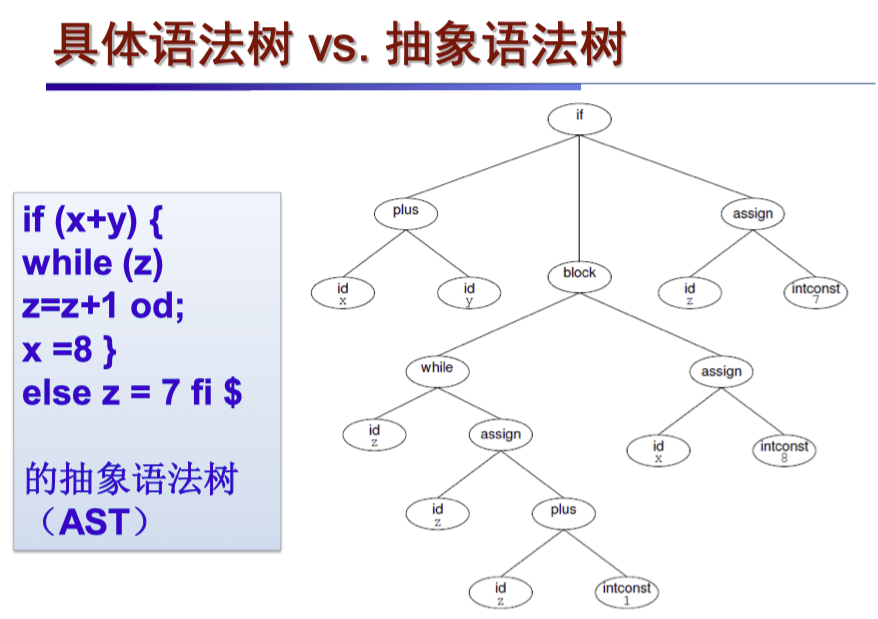
可以看到,AST 相较于具体语法树,不再包含标点符号等非本质的东西,而且不再像具体语法树一样表示为推导的完整过程,而是带有了一部分的语义信息。
抽象语法树的构造#
定义:抽象语法树中的每个结点代表一个程序构造,子结点代表构造的组成部分。
例如,表达式 E1+E2 的语法树结点标号为 +,子结点分别代表 E1 和 E2。
结点构造: 每个结点有一个 op 字段表示结点标号,及以下字段:
- 叶子结点(Leaf):
- 有一个附加域存储此叶子结点的词法值
- 构造函数 Leaf(op,val) 创建叶子结点对象
- 例如:Leaf(num,5) 表示一个叶子结点,标号为 num,值为 5
- 内部结点(Node):
- 附加字段数量等于结点的子结点数量
- 构造函数 Node(op,c1,c2,...,ck) 创建内部结点对象
- 例如:Node(+,E1,E2) 表示一个内部结点,标号为 +,子结点为 E1 和 E2
总结:
- 抽象语法树结点通过 op 字段表示 标号,叶子结点通过 val 存储 值,内部结点通过 构造函数 Node 连接子结点
- 属性 E.node 指向 E 对应的这一块 以之为根节点的语法树 的一部分
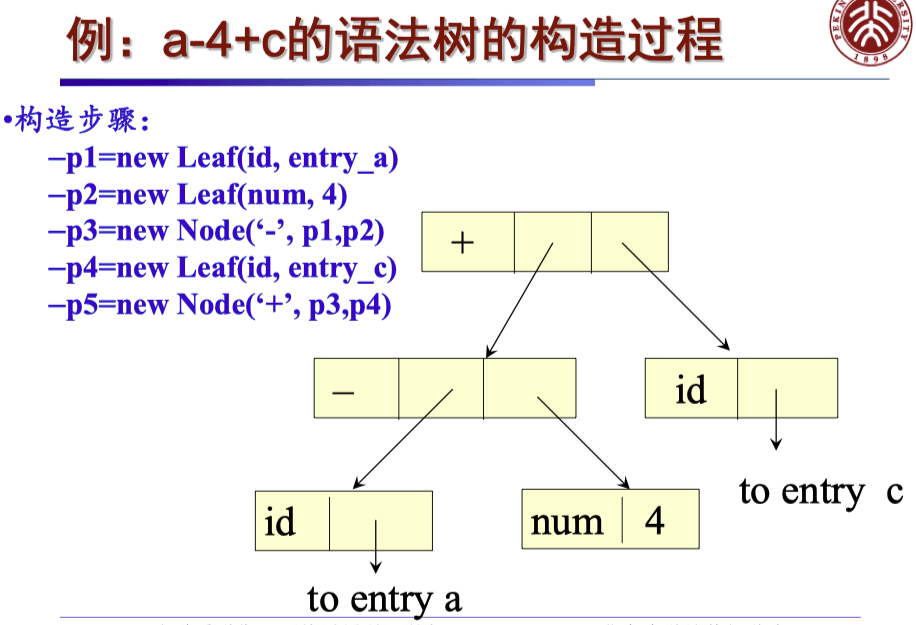
自顶向下的 AST 构造过程#
1)2)3)4)5)6)7)产生式E→TE′E′→+TE1′E′→−TE1′E′→εT→(E)T→idT→num语义规则E.node=E′.synE′.inh=T.nodeE1′.inh=new Node(′+′,E′.inh,T.node)E′.syn=E1′.synE1′.inh=new Node(′−′,E′.inh,T.node)E′.syn=E1′.synE′.syn=E′.inhT.node=E.nodeT.node=new Leaf(id,id.entry)T.node=new Leaf(num,num.val)
对于式子 a−4+c,构造出语法分析树如下:
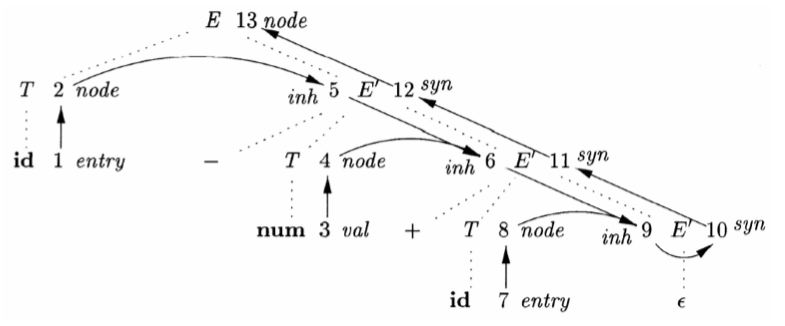
注意:
- 最后一列语义规则不一定是同时执行的,如在产生式(1)中,实际上先计算了继承属性 E′.inh=T.node,但是在最后才计算综合属性 E.node=E′.syn。
- 一个文法符号可能对应多个结点,如图里结点 4、8 都对应同一个 T
- 虚线部分构成的是一颗 语法分析树,而不是 抽象语法树
注意这张图中实际上有个关系:
- 虚线:语法分析树
- 黑线:依赖图,依赖图中的边表示的是依赖关系,而不是等于关系
非终结符号 E′ 有一个继承属性 inh 和一个综合属性 syn。
属性 inh 表示至今为止构造得到的部分抽象语法树
举例:E′.inh 表示的是位于 E′ 的子树左边的输入串前缀所对应的抽象语法树的根
- 在图中的结点 5 处,E′.inh 表示对应于节点 2(a)的抽象语法树的根
- 在节点 6 处则对应节点 5(a−4)
- 在节点 9 处则对应节点 6(a−4+c),因为没有更多的输入,所以在结点 9 处,E′.inh 指向整个抽象语法树的根
继承属性可以把值从一个结构传递到另一个并列的结构,也可把值从父结构传递到子结构。
属性 syn 把这个值沿着语法分析树向上传递,直到它成为 E.node 的值
举例:
- 结点 10 上的属性值 E′.syn 是通过产生式 4 所关联的规则 E′.syn=E′.inh 来定义的
- 结点 11 处的属性值 E′.syn 是通过产生式 2 所关联的规则 E′.syn=E1′.syn 来定义的
- 类似的规则还定义了结点 12 和 13 处的值
语法制导的翻译方案(SDT)#
定义:语法制导的翻译方案(syntax-directed translation scheme,SDT)是对语法制导定义的补充,也称作语法制导的翻译模式。
- 把 SDD 的 语义规则改写为计算属性值的程序片段,用花括号 {} 括起来,插入到产生式右部的任何合适的位置上
- 这种方法表示语法分析和语义动作交错,可以在按 深度优先 遍历分析树的过程中随时执行语义动作
说人话:
- SDT 是在语法分析过程中附带语义动作(程序计算片段)
- 语义动作可以放在产生式的任意位置,通常用大括号 {} 包围
基础文法:原来的不含语义动作的文法称作基础文法。
一个简单的 SDT (只包含 +/- 操作的表达式):
E→R→∣T→TRaddop T{print(addop.lexeme)}R1εnum{print(num.val)}
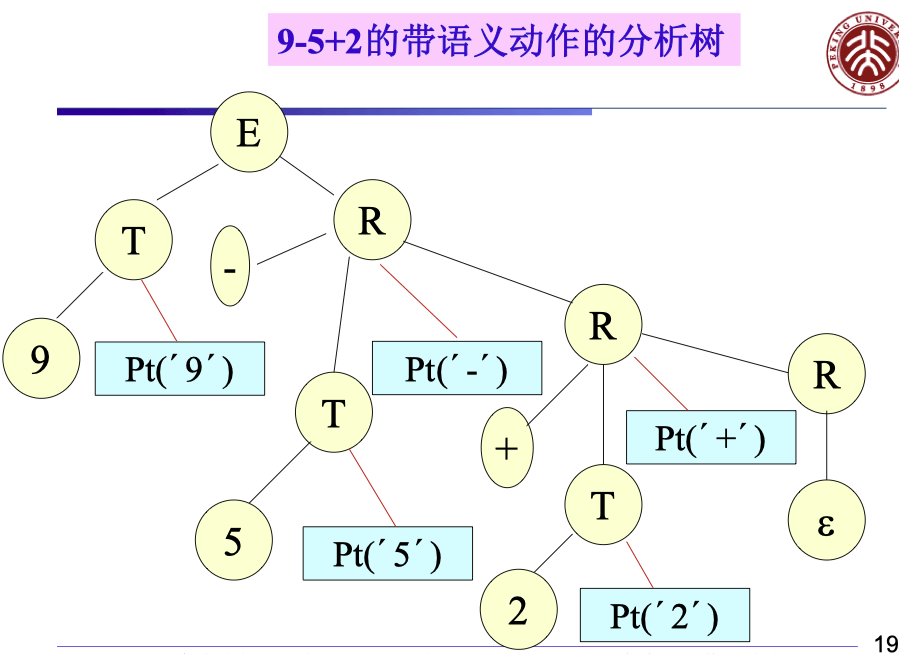
图中 pt 即 print,以深度优先搜索遍历这颗树的时候,即得到后缀表达式。
SDT 的实现方法#
基本实现方法:
- 建立语法分析树
- 将语义动作看作是虚拟的结点
- 从左到右,深度优先地遍历分析树,在访问虚拟结点时执行相应动作
通常情况下在语法分析过程中实现,不需要真的构造语法分析树。
实现 SDD 的两种重要基础文法:
翻译方案的设计#
- 根据语法制导定义设计翻译方案
- 需要保证语义动作不会引用还没有计算的属性值
只需要综合属性的情况#
操作:为每一个语义规则建立一个包含赋值的动作,并把这个动作放在相应的产生式右边的末尾。
例如:
T→T1∗F
所需动作:T.val=T1.val∗F.val
改写后:
T→T1∗F{T.val=T1.val∗F.val}
既有综合属性又有继承属性#
原则:
-
产生式 右边 的符号的 继承属性 必须在 这个符号以前 的动作中计算出来(不然上哪里去继承?)
-
一个动作 不能引用 这个动作 右边符号的综合属性 (还没算到右边符号呢)
继承属性肯定得允许,不然你赋值 {A1.in=1}A1 都不行。
-
产生式 左边非终结符号的综合属性 只有在它所 引用的所有属性都计算出来 以后才能计算
计算这种属性的动作通常可放在产生式右端的末尾(同上文只需要综合属性的情况)
例如:
S→A1A2{A1.in=1;A2.in=2}A→a{print(A.in)}
此翻译方案不满足要求(违背原则 1,应该在 A1 出现之前,先算出其继承属性 A1.in),可以改成如下的形式:
S→{A1.in=1}A1{A2.in=2}A2A→a{print(A.in)}
后缀翻译方案#
后缀 SDT:所有动作都在产生式最右端的 SDT
文法可以自底向上分析且 SDD 是 S 属性的,必然可以构造出后缀 SDT。
构造方法:
- 将每个语义规则看作是一个赋值语义动作
- 将所有的语义动作放在规则的 最右端

后缀 SDT 的语法分析栈实现#
实现方法:可以在 LR 语法分析的过程中实现。
- 归约时 执行相应的语义动作
- 定义用于记录各文法符号的属性的 union 结构
- 栈中的每个文法符号(或者说状态)都附带一个这样的 union 类型的值
在按照产生式 A→XYZ 归约时,Z 的属性可以在栈顶找到,Y 的属性可以在下一个位置找到,X 的属性可以在再下一个位置找到。
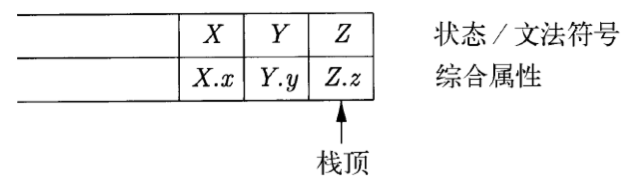

上图展示了一个规约的过程,把 XYZ 规约回了 A,并在此过程中完成了属性的传递。

再次强调:这是自底向上的分析过程,语义动作在规约时生效。
产生式内部带有语义动作的 SDT#
B→X{a}Y
动作左边的所有符号(以及动作)处理完成后 ,就立刻执行这个动作。
- 自底向上分析时,(最早就开始)在 X 出现在栈顶(即刚刚规约出 X)时执行动作 a
- 自顶向下分析时,(延迟到最晚)在试图展开 Y 或者在输入中检测到 Y 的时候执行 a
有问题的 SDT#
并不是所有的 SDT 都可以在分析过程中实现。
比如,从中缀表达式到前缀表达式的转换:
1)2)3)4)5)6)7)L→EnE→{print(“+”);}E1+TE→TT→{print(“*”);}T1∗FT→FF→(E)F→digit{print(digit.lexval);}
在自顶向下和自底向上的分析中都无法实现这种 SDT:
在这个 SDT 中,操作符(+ 和 *)需要在操作数之前打印,这就是将中缀表达式转换为前缀表达式的要求。然而:
-
在自顶向下分析中:
- 分析过程是从左到右进行的
- 当遇到产生式 E→E1+T 时,必须先处理 E1
- 但是根据语义动作的要求,我们需要在处理 E1 之前就打印“+”
- 这造成了时序上的矛盾
-
在自底向上分析中:
- 分析过程是按照规约顺序进行的
- 当要规约 E1+T 到 E 时,E1 和 T 的值已经计算完成
- 此时再打印“+”就太晚了,因为操作数已经处理完毕
所以,对于这种一般的 SDT,可以先建立分析树(语义动作作为虚拟的结点),然后进行前序遍历并执行动作。
消除左递归时 SDT 的转换方法#
如果动作不涉及属性值,可以 把动作当作终结符号 进行处理,然后消左递归。
原始的产生式:
EE→E1+T{print(“+”)}→T
转换后得到:
ERR→TR→+T{print(“+”)}R→ε
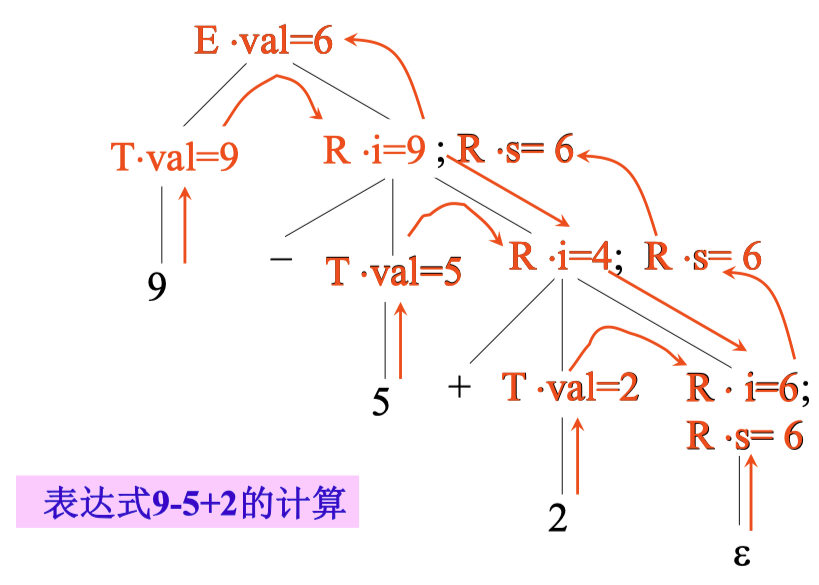
左递归文法翻译方案的转换#
带左递归的文法:
EEETT→E1+T{E.val=E1.val+T.val}→E1−T{E.val=E1.val−T.val}→T{E.val=T.val}→(E){T.val=E.val}→num{T.val=num.val}
转换后的不带有左递归的文法:
ERRRTT→T{R.i=T.val}R{E.val=R.s}→+T{R1.i=R.i+T.val}R1{R.s=R1.s}→−T{R1.i=R.i−T.val}R1{R.s=R1.s}→ε{R.s=R.i}→(E){T.val=E.val}→num{T.val=num.val}
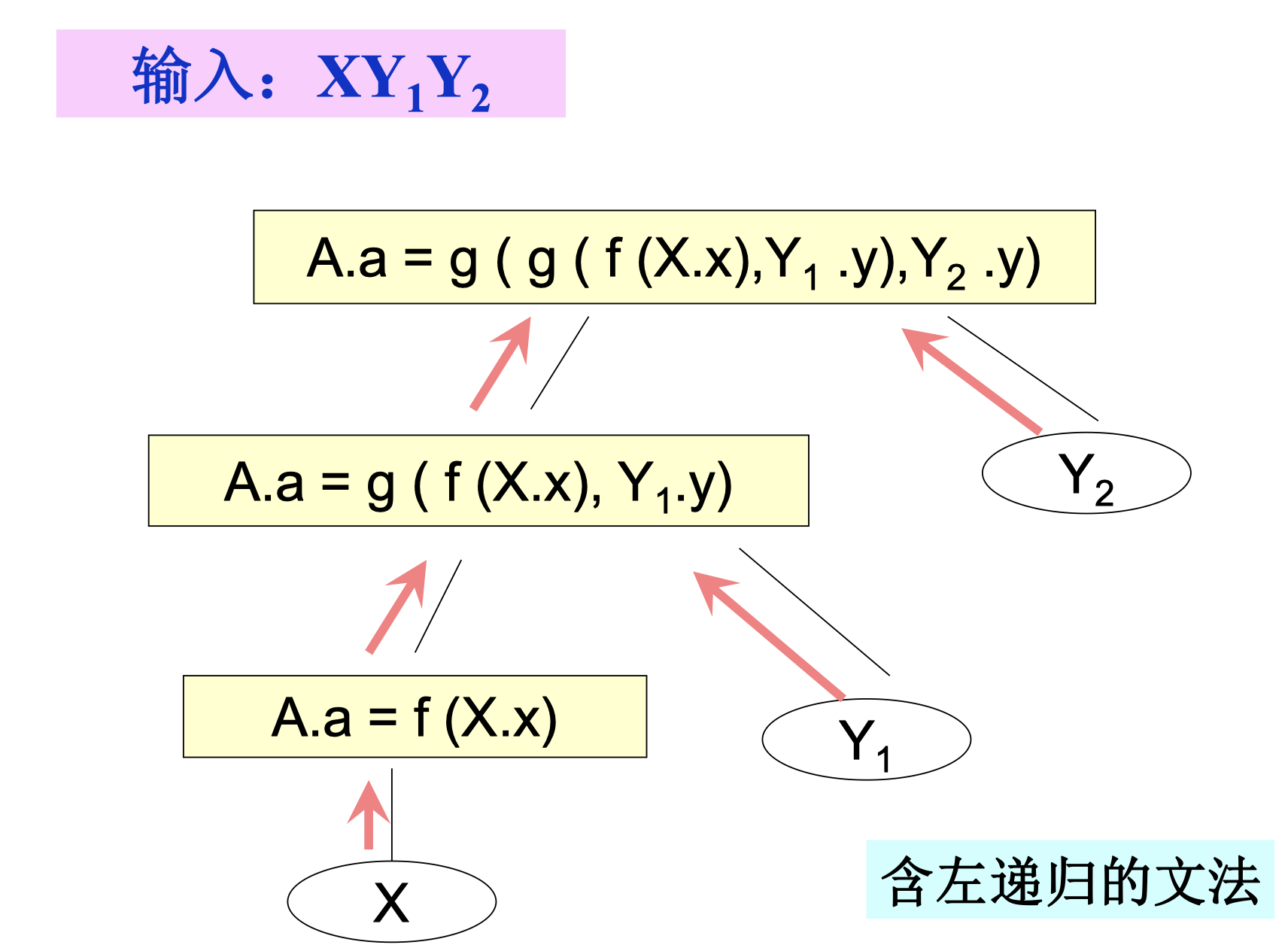
原有文法:
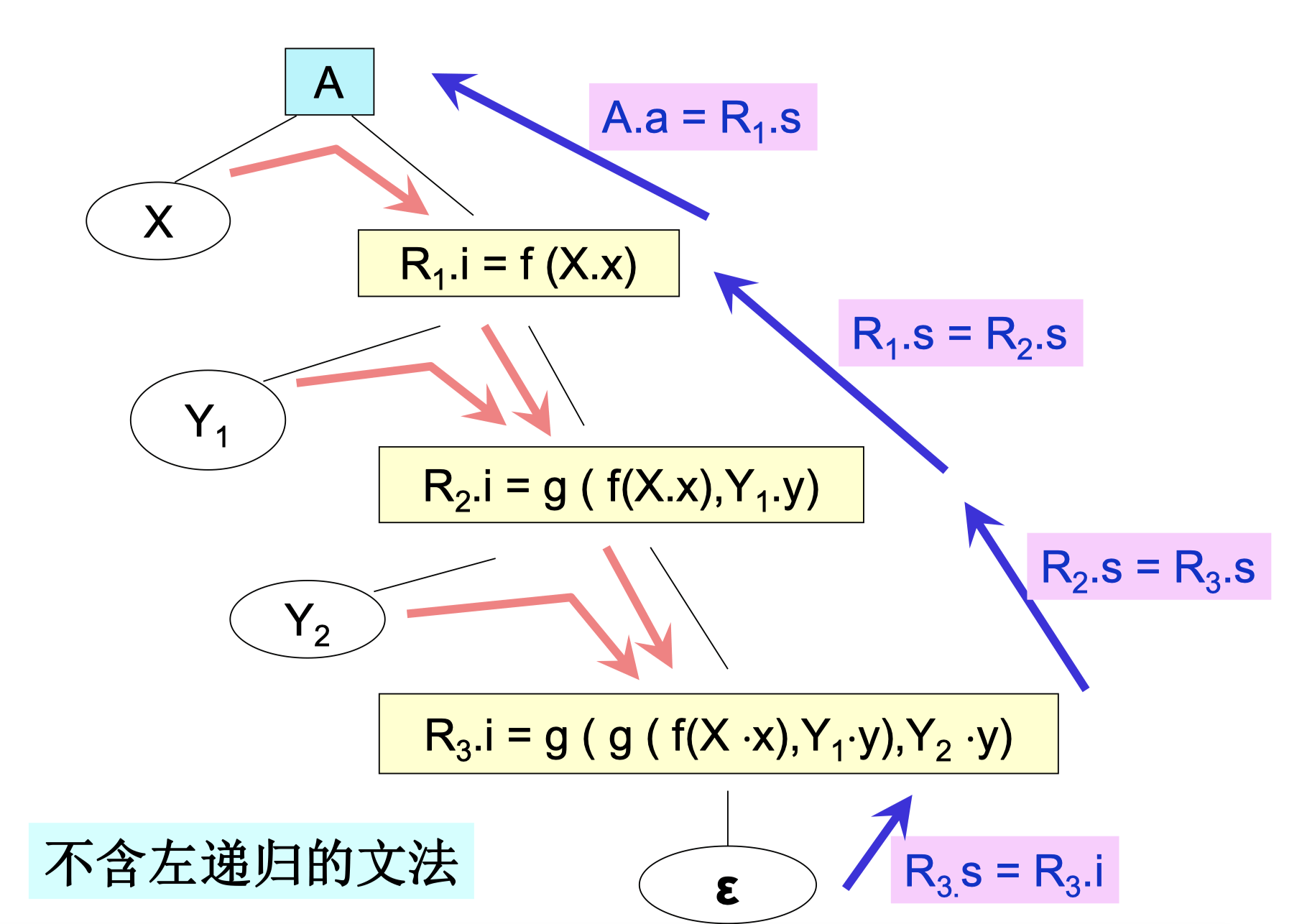
AA→A1Y{A.a=g(A1.a,Y.y)}→X{A.a=f(X.x)}
消除左递归之后,文法转换成
A→XRR→YR∣ε
消除左递归后的翻译方案:
ARR→X{R.i=f(X.x)}R{A.a=R.s}→Y{R1.i=g(R.i,Y.y)}R1{R.s=R1.s}→ε{R.s=R.i}
注意事项#
- 并不是所有的 SDT 都可以在分析过程中实现
- 后缀 SDT 以及 L 属性 SDT 可以在分析时完成











