程序优化

代码优化概述

代码优化的原则：

• 保证安全（确保语义 / 可观察行为不变）
• 提高效率（二八法则：80% 时间在 20% 代码上，主要优化这 20% 代码）

优化方式：

• 算法设计阶段
• 编译阶段
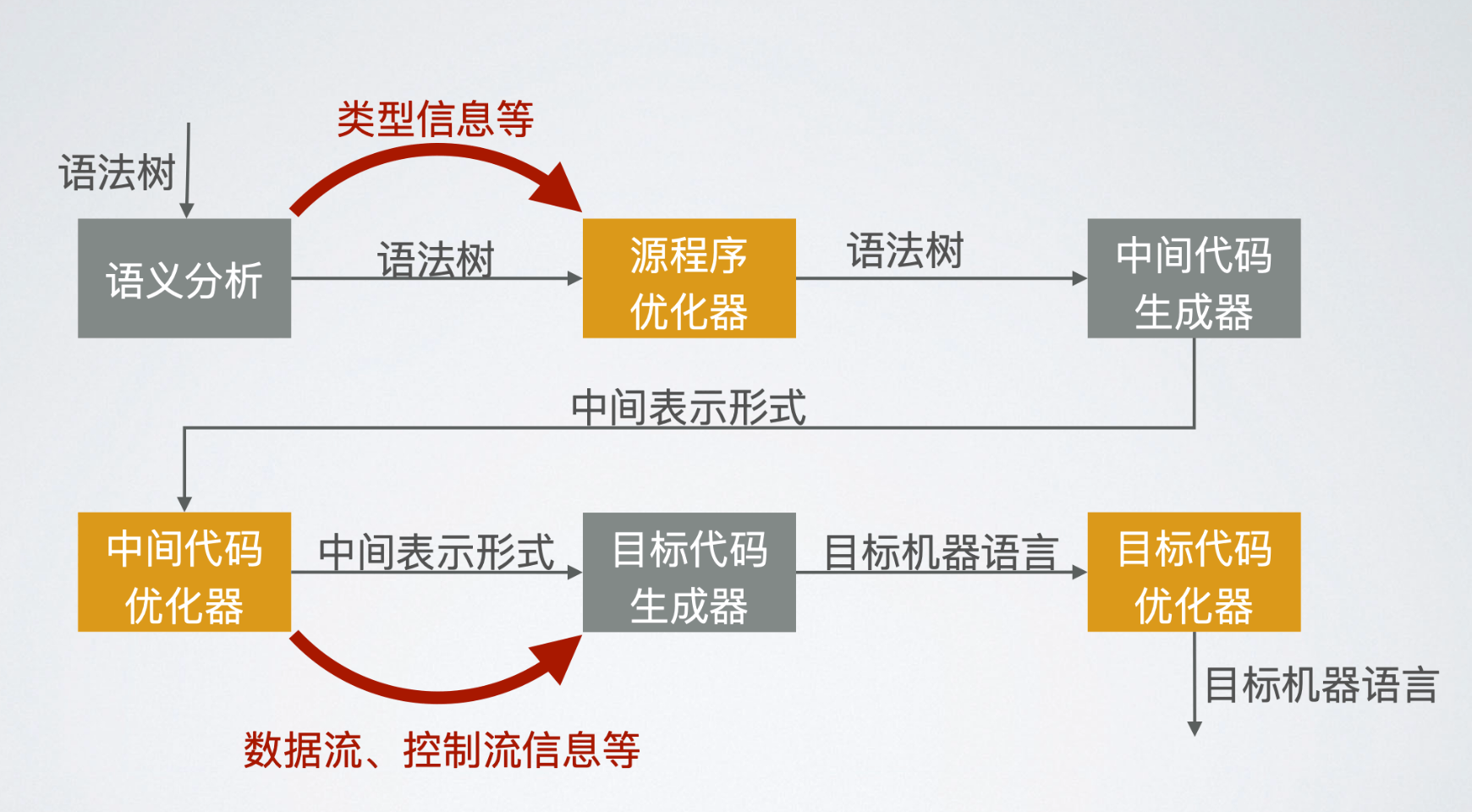
• 语义分析：根据静态检查，优化 源程序
• 中间代码生成：机器无关优化
• 目标代码生成：机器有关优化
• 链接时刻优化

代码优化器的结构

代码优化的范围

• 局部优化：基本块内（即标号分割的块）
• 区域性优化：若干个基本块构成的区域
• 全局优化：一个过程内所有基本块
• 过程间优化：一个程序所有过程及其基本块

代码优化的常用方法

• 公共子表达式消除
• 复写传播（消除 a=b）
• 死代码消除
• 常量折叠 / 常量传播：直接推导出表达式的值是否为常量，若为常量则直接用其替换该表达式
• 代码外提（循环中不变量外提）
  • 循环不变式：不管循环执⾏多少次都得到相同结果的表达式
• 强度消减：减少操作次数、操作强度（如将二的幂次乘除法转换为移位操作）
  • 归纳变量：每次循环都增加恒定常数的变量
  • 如果一组归纳变量变化步调一致，考虑消除一些
• 数据流分析

数据流分析

数据流分析是一种静态代码分析技术，用于在程序编译时推导出程序各部分可能的行为。它通过分析变量和表达式在程序中的流动情况，帮助我们理解程序在不同点上的状态。

一些基本概念：

1. 基本块（Basic Block）：一个基本块是一段没有分支和跳转的连续代码。换句话说，它是一个入口和一个出口之间的代码段，只有在入口处进入，并且在出口处离开。
2. 控制流图（Control Flow Graph, CFG）：控制流图是由基本块作为节点，控制流作为边构成的有向图。它展示了程序执行的所有可能路径。

通过数据流方程，计算每个基本块的入口和出口状态。常见的数据流方程包括：

• 到达定义（Reaching Definitions）：哪些变量定义可以到达这个基本块。
• 活跃变量（Live Variables）：哪些变量在基本块之后仍然需要使用。
• 可用表达式（Available Expressions）：哪些表达式在基本块入口处已经计算过且没有被修改。

数据流抽象

基本概念：

• 程序点（program point）：每条语句对应其前、后两个程序点
  • 基本块内两条语句 $s_1, s_2$，$s_1$ 后的程序点与 $s_2$ 前的程序点相同
• 路径（path）：程序点 $p_1, p_2, \ldots, p_n$ 构成的序列，对于任意 $1 \leq i < n$，必然有二者之一（人话就是他们连着）：
  • 点 $p_i$ 和点 $p_{i+1}$ 是一条语句前、后的两个程序点
  • 点 $p_i$ 指向基本块的结尾，点 $p_{i+1}$ 指向该基本块后继的开头（连接不同基本块）

数据流分析推导

对于每个程序点 $p$:

• 前向（forward）分析：以 $p$ 为终点的所有路径的集合的性质（人话就是顺着逻辑流走）
• 后向（backward）分析：以 $p$ 为起点的所有路径的集合的性质（人话就是逆着逻辑流走）

前向分析模式

• 数据流分析的域 $V$，交汇运算 $\wedge: V \times V \rightarrow V$，顶值 $T \in V$
• 每个基本块 $B$ 的传递函数 $f_B: V \rightarrow V$ （从入口到出口）
• 边界条件：$\text{OUT}[\text{ENTRY}] = \nu_{\text{ENTRY}}$
• 初始值：$\text{OUT}[B] = T \quad (B \neq \text{ENTRY})$
• 方程组：对任意 $B \neq \text{ENTRY}$，有 $$\begin{aligned} &\text{IN}[B] = \bigwedge_{P \text{是} B \text{的前驱}} \text{OUT}[P] \\ &\text{OUT}[B] = f_B(\text{IN}[B]) \end{aligned}$$

后向分析模式

• 数据流分析的域 $V$，交汇运算 $\wedge: V \times V \rightarrow V$，顶值 $T \in V$（即不清楚值时的默认输入）
• 每个基本块 $B$ 的传递函数 $f_B: V \rightarrow V$ （从出口到入口）
• 边界条件：$\text{IN}[\text{EXIT}] = \nu_{\text{EXIT}}$
• 初始值：$\text{IN}[B] = T \quad (B \neq \text{EXIT})$
• 方程组：对任意 $B \neq \text{EXIT}$，有 $$\begin{aligned} &\text{OUT}[B] = \bigwedge_{S \text{是} B \text{的后继}} \text{IN}[S] \\ &\text{IN}[B] = f_B(\text{OUT}[B]) \end{aligned}$$

活跃变量分析

活跃变量：在程序点 $p$ 之后仍然需要使用的变量

• 分析模式：后向分析模式
• 基础定义：
  • $\text{def}_B$：基本块 $B$ 中定义的变量
  • $\text{use}_B$：基本块 $B$ 中使用的变量
• 分析域 $V$：变量集
• 交汇运算 $\land$： $$O_1 \land O_2 = O_1 \cup O_2$$ 即：在任意后继中活跃则认为是活跃的。
• 顶值 $T$：$\varnothing$
• 传递函数 $f_B$：$f_B(O) = (O - \text{def}_B) \cup \text{use}_B$
• 方程组： $$\begin{aligned} &\text{OUT[B]} = \bigcup_{\text{s是B的后继}} \text{IN[S]} \\ &\text{IN}[B] = \text{OUT}[B] \cup \text{use}_B \end{aligned}$$

注意传递函数实际上是指令级一条套一条推得的：

所以如果你是直接根据块级别去做题的话，需要额外注意各条指令之间的依赖关系，判断到底是先用还是先定义。

比如说：

这个基本块中，我们不仅定义了 $a$，还使用了 $a$，但是由于我们是先定义的，所以 $a$ 不在这个块最终输出的活跃变量中。

又比如：

这个基本块中，我们也是既定义了 $a$，又使用了 $a$，但是仔细观察会发现我们是先使用的 $a$，再定义的 $a$，所以 $a$ 在这个块最终输出的活跃变量中。

后续分析同，不再赘述。

到达定值分析

到达定值（可达定义）：在程序点 $p$ 处，变量 $v$ 的定值（即赋值语句，$v = \text{exp}$）可以到达 $p$

• 分析模式：前向分析模式
• 基础定义：
  • $\text{gen}_B$：基本块 $B$ 中生成定值的集合
  • $\text{kill}_B$：基本块 $B$ 中杀死定值的集合，即对于基本块中定值的 $v$，杀死所有其他对 $v$ 的定值
• 分析域 $V$：变量集
• 交汇运算 $\land$： $$I_1 \land I_2 = I_1 \cup I_2$$ 即：在任意前驱可达则认为是可达的。
• 顶值 $T$：$\varnothing$
• 传递函数 $f_B$：$f_B(I) = (I - \text{kill}_B) \cup \text{gen}_B$
• 方程组： $$\begin{aligned} &\text{IN}[B] = \bigwedge_{P \text{是} B \text{的前驱}} \text{OUT}[P] \\ &\text{OUT}[B] = f_B(\text{IN}[B]) \end{aligned}$$

可用表达式分析

可用表达式：到达一个程序点的每条路径都对表达式 $E$ 求值，并且该表达式最近一次求值后其使用的变量没有被修改。

• 分析模式：前向分析模式
• 基础定义：
  • $\text{e\_gen}_B$：基本块 $B$ 中生成的表达式的集合
  • $\text{e\_kill}_B$：基本块 $B$ 中杀死的表达式的集合，若基本块中有语句 $s$ 对 $x$ 赋值，则杀死所有使用 $x$ 的表达式，如 $z = x + y$ 会杀死 $z + 1$，又如 $x = x + y$ 会杀死 $x + y$
• 分析域 $V$：表达式集
• 交汇运算 $\land$： $$I_1 \land I_2 = I_1 \cap I_2$$ 即：要求任意前驱中都要可用才认为可用
• 顶值 $T$：全集
• 传递函数 $f_B$：$f_B(I) = (I - \text{e\_kill}_B) \cup \text{e\_gen}_B$
• 方程组： $$\begin{aligned} &\text{IN}[B] = \bigwedge_{P \text{是} B \text{的前驱}} \text{OUT}[P] \\ &\text{OUT}[B] = f_B(\text{IN}[B]) \end{aligned}$$

注意：

这个基本块中，我们也是既计算了 $a + b$，又定值了 $a$，后来的定值杀死了前面的计算，所以 $\text{e\_gen}_B$ 不包括 $a+1$，但是 $\text{e\_kill}_B$ 包括 $a+1$（这样做能满足传递函数定义）。

总结

其中：

• $B$ 表示基本块，$S$ 表示后继块，$P$ 表示前驱块
• $\text{def}_B$ 表示在块 $B$ 中定义的变量集合
• $\text{use}_B$ 表示在块 $B$ 中使用的变量集合
• $\text{kill}_B$ 表示在块 $B$ 中被覆盖的定义集合
• $\text{gen}_B$ 表示在块 $B$ 中生成的定义集合
• $\text{e\_kill}_B$ 表示在块 $B$ 中被覆盖的表达式集合
• $\text{e\_gen}_B$ 表示在块 $B$ 中生成的表达式集合

习题

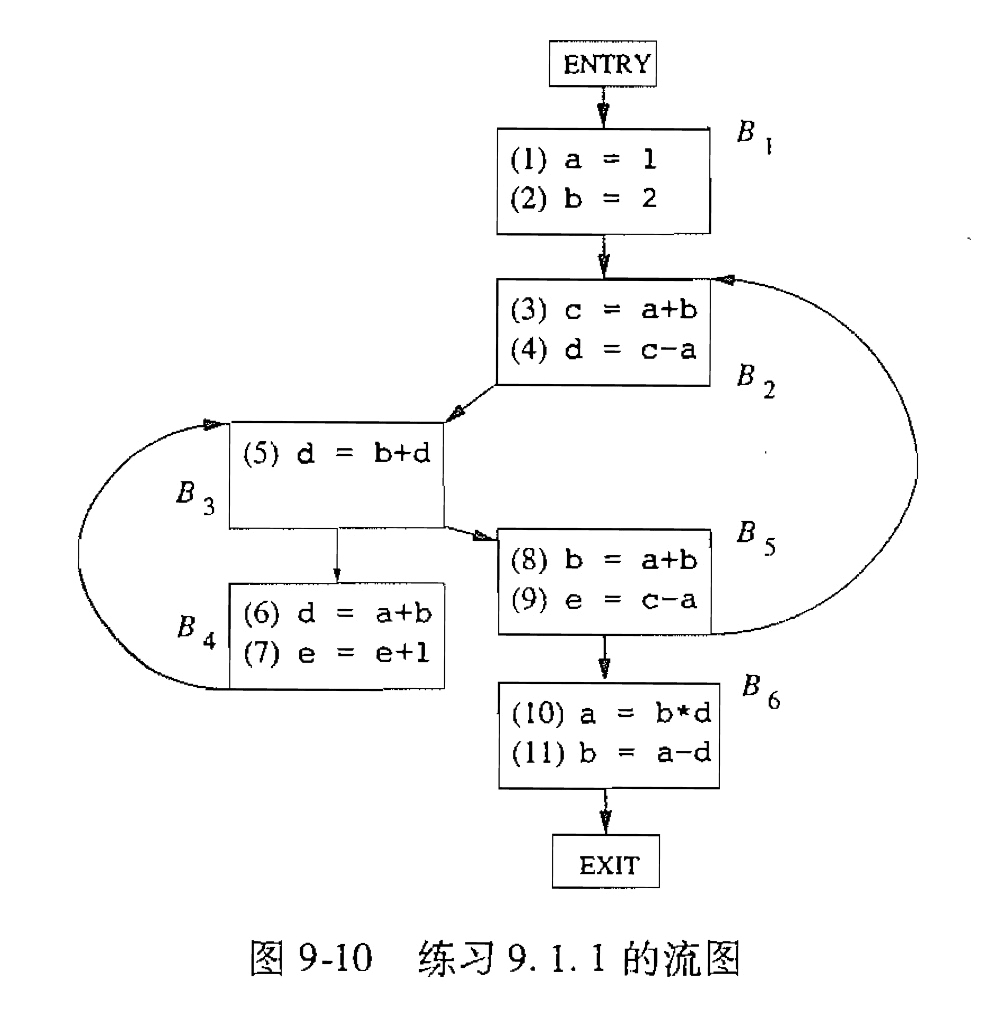
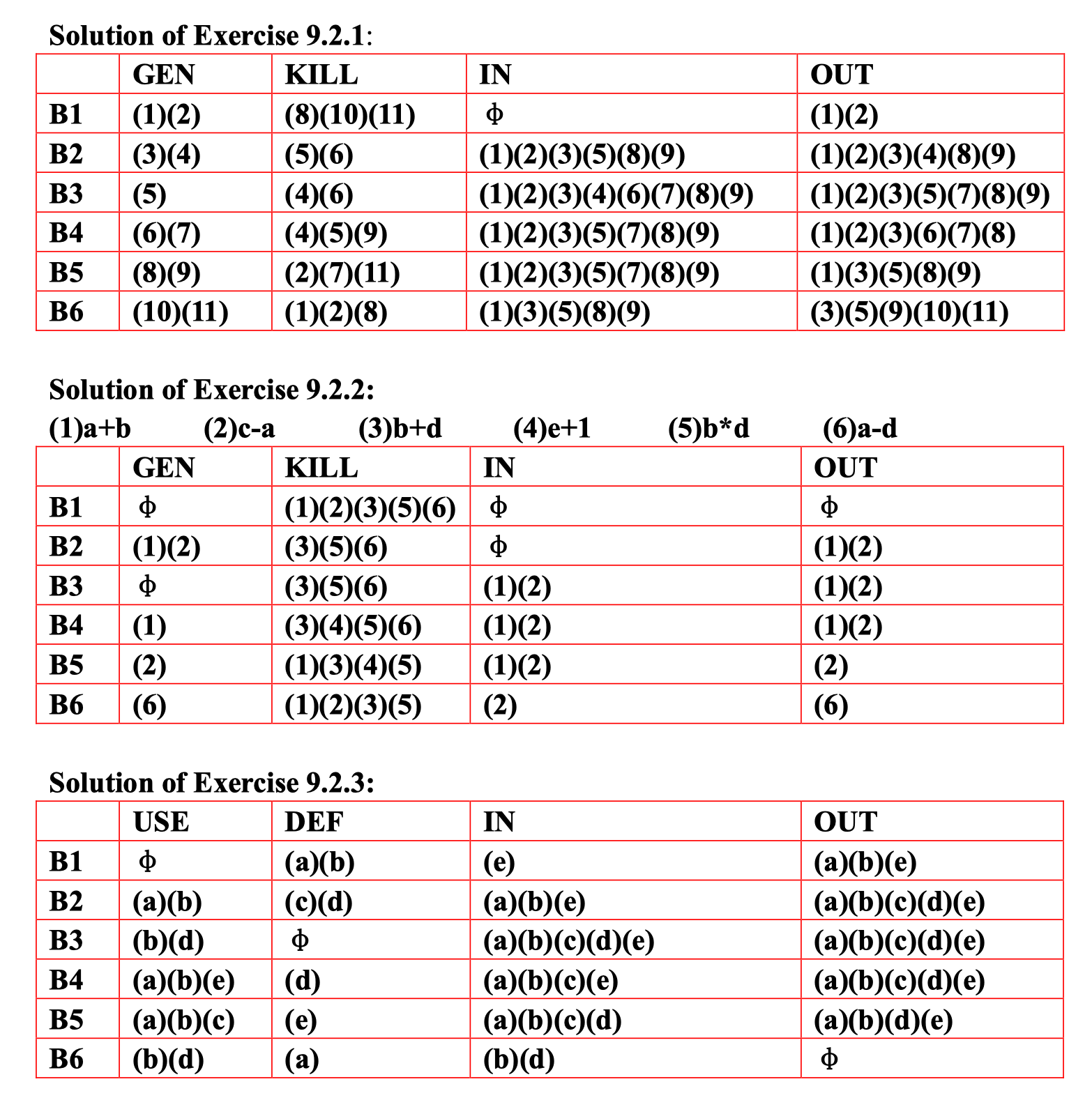
做数据流分析的结果：

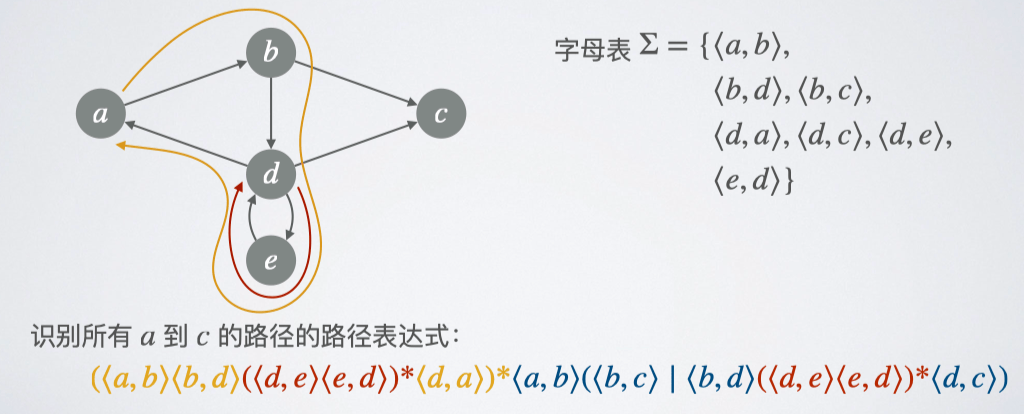
路径表达式

• 有向图 $G = (V, E)$：其中 $V$ 是顶点集合，$E$ 是边的集合。
• 路径表达式 （path expression）：一个以 $E$ 为字母表的正则表达式 $R$，且 $R$ 识别的每个符号串都是图 $G$ 中的一条路径。

基于路径表达式的数据流分析

• 数据流分析的域 $V$，交汇运算 $\wedge : V \times V \to V$
• 每个基本块 $B$ 的传递函数 $f_B : V \to V$
• 用 $F(R) : V \to V$ 表示 $R$ 能识别的路径的数据流抽象

以前向分析为例

• $F(\varepsilon)$ = 恒等函数
• $F(e) = f_{h(e)}$，其中 $h(e)$ 是边 $e$ 的起点基本块
• $F(R_1 \mid R_2) = F(R_1) \wedge F(R_2)$
• $F(R_1 R_2) = F(R_2) \cdot F(R_1)$
• $F(R_1^*) = \bigwedge_{i \geq 0} F(R_1)^i$，不过有时能找到更高效的算法