目标代码生成 • Arthals' ink

目标机模型

类 RISC 计算机，按字节寻址，以 4 个字节为 1 个字（word）
通用寄存器 $R_1, R_2, ⋯, R_n$
使用如下机器指令，每条指令的长度为 8 字节：
- $\text{LD} \; \text{dst}, \text{addr}$ ：把位置 $\text{addr}$ 上的值加载到位置 $\text{dst}$ （load）
  $\text{LD} \; r_1, r_2$ ：寄存器到寄存器的拷贝
- $\text{ST} \; x, r$ ：把寄存器 $r$ 中的值保存到位置 $x$ （store）
- $\text{OP} \; \text{dst}, \text{src}_1, \text{src}_2$ ：把位置 $\text{src}_1$ 和 $\text{src}_2$ 中的值运算后将结果放到位置 $\text{dst}$ 中（operation）
  $\text{OP}$ 是诸如 $\text{ADD}$ 或 $\text{SUB}$ 的运算符
- $\text{BR} \; L$ ：控制流转向标号为 $L$ 的指令（branch）
- $\text{Bcond} \; r, L$ ：对寄存器 $r$ 中的值进行测试，如果为真则转向标号 $L$ （branch condition）
  $\text{cond}$ 是诸如 LTZ（判断是否小于 0）或 NEZ（判断是否不等于 0）的常见测试

目标机的寻址模式

contents(addr) 表示 addr 所代表的位置中的内容
lvalue(x) 表示分配给变量 x 的内存位置

位置形式	汇编表示	地址
变量名	`x`	`lvalue(x)`
数组索引	`a(r)`	`lvalue(a) + contents(r)`
直接常数	`#M`	`M`
寄存器	`r`	`r`
间接寄存器	`*r`	`contents(r)`
索引	`M(r)`	`M + contents(r)`
间接寄存器索引	`*M(r)`	`contents(M + contents(r))`

target_machine_addressing_mode

进行栈式管理的目标代码

生成支持栈式存储管理的目标代码：

生成过程调用和返回的目标代码序列
将 IR 中的名字转换成为目标代码中的地址

简化调用 / 返回的三地址代码：

call callee
return

过程 callee （被调用者）的属性（编译时确定）：

callee.codeArea：运行时代码区中 callee 的第一条指令的地址
callee.recordSize：callee 的一个活动记录的大小

过程的调用和返回

简化场景下的活动记录：

只需考虑在活动记录中保存返回地址
假设寄存器 SP 中维持一个指向栈顶的指针

调用指令序列

调用者

ST -4(SP), #here + 16：计算返回地址，当前指令地址加上 16（偏移掉 2 条指令，即当前 ST 和下一条 BR），地址是 4 字节的（32 位）
BR callee.codeArea：跳转到被调用者的代码

被调用者

SUB SP, SP, #callee.recordSize：为活动记录分配空间

返回指令序列

被调用者

ADD SP, SP, #callee.recordSize：释放活动记录
BR *-4(SP)：跳转到返回地址

指令选择

控制流图

基础定义：

基本块（Basic Block）：一个基本块是一段没有分支和跳转的连续代码。换句话说，它是一个入口和一个出口之间的代码段，只有在入口处进入，并且在出口处离开。
具有线性结构，其中最后一条语句为跳转或者过程 / 函数返回 （br /jump/ret）。
控制流图（Control Flow Graph, CFG）：控制流图是由基本块作为节点，控制流作为边构成的有向图。它展示了程序执行的所有可能路径。
有向图，图中结点为基本块，边为控制流跳转。控制流只能从基本块的第一条指令进入。

示例代码：

n = 10; a = 1; b = 1;
while (!(n == 0)) {
    t = a + b; a = b; b = t;
    n = n - 1;
}
return a;

对应的控制流图：

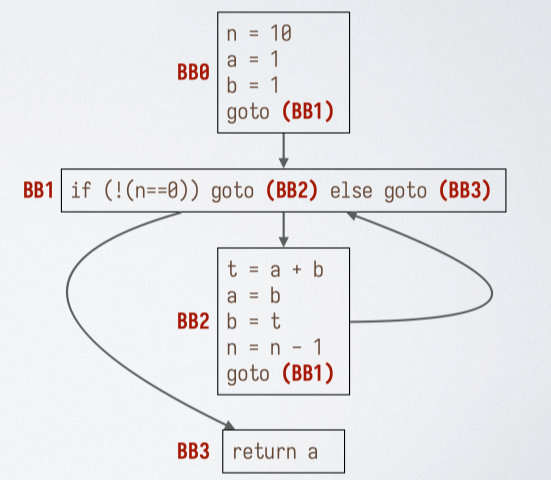
62038

控制流图 + 三地址代码

三地址代码：控制流图的每个基本块内部为三地址代码。

跳转指令的目标为基本块（而不是指令标号）。
一种常见的 混合 IR。
上图 BB1 的指令并不完全是三地址形式，因为（BB2）和（BB3）都不是真实指令标号。

控制流图中的循环

循环的定义：

一个 结点集合 $L$
存在一个 循环入口 （loop entry）结点，唯一的前驱可以在 $L$ 之外的结点
每个结点都有到达入口结点的非空路径，且该路径都在 $L$ 中

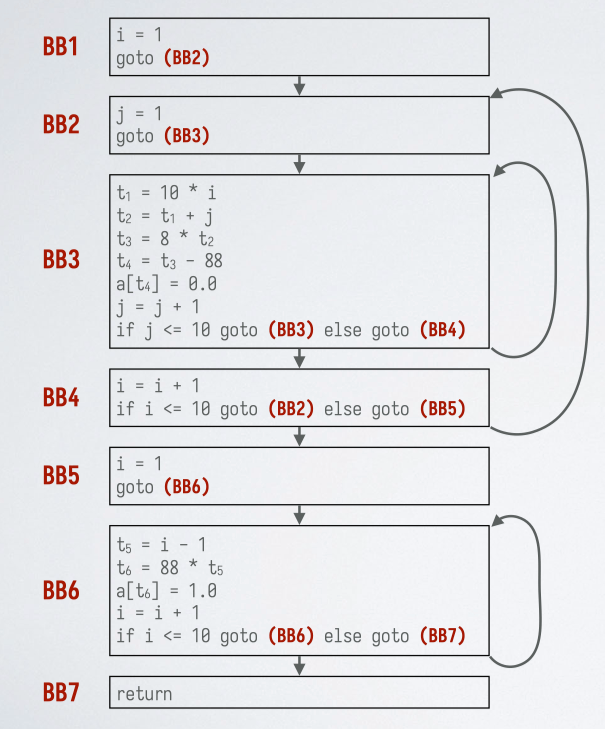
30799

对应的控制流图中的循环：

循环 1： $\{BB3\}$
循环 2： $\{BB6\}$
循环 3： $\{BB2, BB3, BB4\}$ （BB2 为入口结点）

划分基本块的算法

输入：三地址指令序列。

输出：基本块的列表。

方法：

确定 首指令 （leader，基本块的第一条指令）：
- 第一条三地址指令。
- 任何一个条件或无条件跳转指令的 目标指令。
- 紧跟在一个条件或无条件跳转指令 之后的指令。
确定基本块：每条首指令对应一个基本块：从首指令开始到下一个首指令。

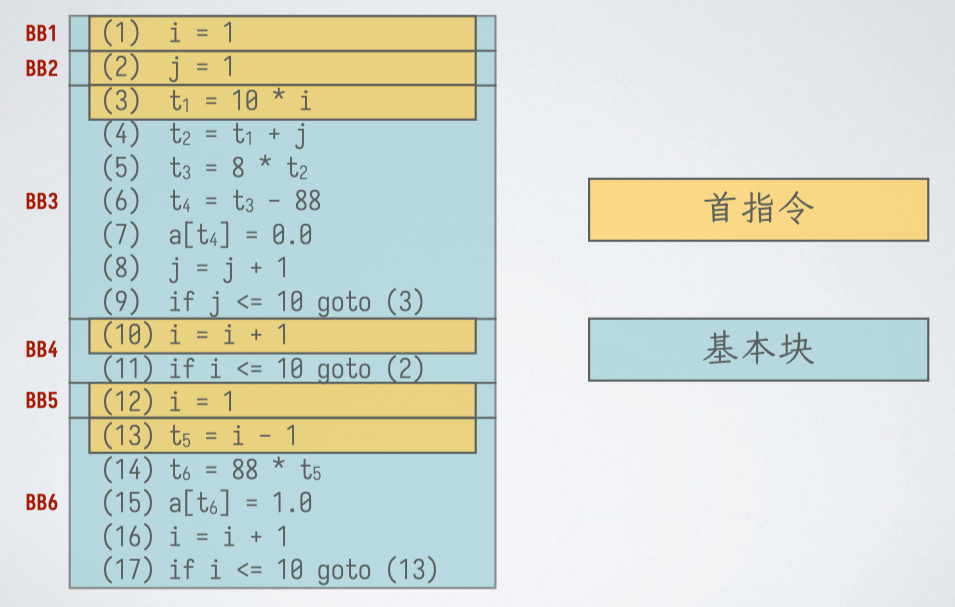
21694

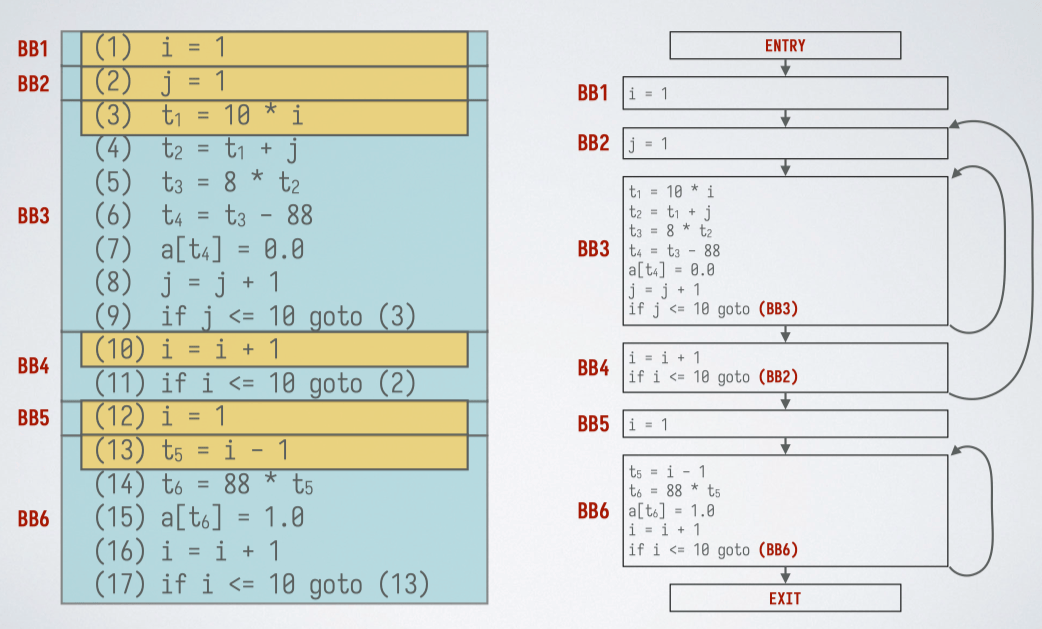
基于三地址跳转指令的流图：两个基本块 $B$ 和 $C$ 之间存在一条有向边当且仅当基本块 $C$ 的第一条指令可能在 $B$ 的最后一条指令之后执行。

情况 1： $B$ 的结尾跳转到 $C$ 的开头。
情况 2： $B$ 的结尾不是无条件跳转，且 $C$ 在原来的序列中紧跟 $B$ 之后。

可以额外添加 入口（entry）和出口（exit）结点，这些结点不包含指令。

64145

指令选择

主要问题：最大限度地利用寄存器，减少与内存交互的加载与保存。

代码生成算法的基本思想：

生成机器指令的规则：

只有当运算分量（参与计算的变量或常数）不在寄存器中，才从内存载入
尽量保证只有当寄存器中的值不被使用时，才把它覆盖掉（延迟到最后一刻）

记录各个值对应的位置的数据结构：

寄存器描述符（register descriptor）
- 为每个寄存器维护，key 为寄存器名 $R_n$ ，value 为变量名
- 跟踪哪些变量的当前值放在该寄存器内
地址描述符（address descriptor）
- 为每个程序变量维护，key 为变量名 $a,b,\cdots$ ，value 为变量名或寄存器名
- 跟踪哪些位置（寄存器、栈中位置等）可以找到该变量的当前值

30399

三地址指令生成

代码语句

$x = y \; \text{op} \; z$

调用 $\text{getReg}(x = y \; \text{op} \; z)$ ，给 $x, y, z$ 选择寄存器 $R_x, R_y, R_z$ 。
查 $R_y$ 的寄存器描述符，如果 $y$ 不在 $R_y$ 中则生成指令 $\text{LD} \; R_y, y'$ ，其中 $y'$ 是某个存放了 $y$ 的值的内存位置。
对 $z$ 做与上述类似的处理。
生成指令 $\text{OP} \; R_x, R_y, R_z$ ，其中 $\text{OP}$ 对应 $\text{op}$ （比如 $\text{ADD}$ 对应 +）。
更新寄存器和地址描述符。

$x = y$

调用 $\text{getReg}(x = y)$ 总是为 $x$ 和 $y$ 选择相同的寄存器。
如果 $y$ 不在 $R_y$ 中，那么生成指令 $\text{LD} \; R_y, y'$ `，其中 $y'$ 是存放 $y$ 的位置。
更新寄存器和地址描述符。
1. 如果生成了 $\text{LD}$ 指令，则先按照 $\text{LD}$ 的规则处理。
2. $R_y$ 的寄存器描述符：把 $x$ 加入变量集合。
3. $x$ 的地址描述符：只包含 $R_y$ 。

三地址指令

$\text{LD} \; R, x$

$R$ 的寄存器描述符：只包含 $x$ 。
$x$ 的地址描述符： $R$ 作为新位置加入 $x$ 的位置集合。
任何不同于 $x$ 的变量的地址描述符中删除 $R$ 。

$\text{OP} \; R_x, R_y, R_z$

$R_x$ 的寄存器描述符：只包含 $x$ 。
$x$ 的地址描述符：只包含 $R_x$ 。
任何不同于 $x$ 的变量的地址描述符中删除 $R_x$ 。

$\text{ST} \; x, R$

生成这种指令时 $R$ 一定存放了 $x$ 的当前值。
$x$ 的地址描述符：把 $x$ 自己的内存位置加入位置集合。

三地址指令的活跃变量分析

活跃变量分析：基本块的结尾

如果变量 $x$ 在出口处活跃（其值在后续的控制流中会被用到），且查 $x$ 的地址描述符发现其不在自己的内存位置上，则生成指令 $\text{ST} \; x, R_x$ 。
更新寄存器和地址描述符。

如果不想维护这些描述符，可以在任何一条语句结束后都立即把值都写回内存位置

活跃变量分析

目的：研究哪些变量 “接下来马上会用到”。如果用不到，可以从寄存器里踢出。

活跃变量：如果对于两条语句 $i,j$ ，满足 $\text{def}(i, x)$ 且 $\text{use}(j, x)$ ，并且 $i\to j$ 存在一条路径没有其他的对变量 $x$ 的赋值，那么 $j$ 使用了 $i$ 处计算的 $x$ ，称为 $x$ 在语句 $i$ 处活跃，记作 $\text{live}_{out}(i, x)$ 。

定值 $\text{def}(i, x)$ ：语句 $i$ 给变量 $x$ 进行了赋值
使用 $\text{use}(i, x)$ ：语句 $i$ 使用了变量 $x$ 的值
活跃变量 $\text{live}_{out}(i, x)$ ：变量 $x$ 在语句 $i$ 后的程序点上活跃（live）

活跃变量信息的用途：实现寄存器选择函数 $\text{getReg}()$ 。

如果一个寄存器只存放了 $x$ 的值，且 $x$ 在 $i$ 处不活跃，那么这个寄存器在 $i$ 处可以用于其它目的。

分析算法

基本原则：设 $i$ 的下一条语句为 $j$ ：

若 $\text{use}(j, x)$ ，则 $\text{live}(i, x)$ ：若在语句 $j$ 处使用了变量 $x$ ，则在语句 $i$ 处（ $i$ 是 $j$ 的前一个语句） $x$ 是活跃的。
若 $\text{live}(j, x)$ 且 $\neg \text{def}(j, x)$ ，则 $\text{live}(i, x)$ ：若在语句 $j$ 处 $x$ 是活跃的，并且 $x$ 不是在语句 $j$ 处定义的，则在语句 $i$ 处 $x$ 也是活跃的。

活跃变量分析通常通过反向扫描程序的语句来进行，具体步骤如下：

初始化：假设在基本块出口处，所有非临时变量均活跃。
反向扫描：
- 从最后一个语句开始反向扫描基本块中的每个语句。
- 对于形如 $x = y \ \text{op} \ z$ $x = y op z$ 的语句 $i$ $i$ ：
  - 将 $x, y, z$ 到目前为止更新过的活跃信息关联到 $i$ 。
  - 设置 $x$ 为 “不活跃”（因为它刚刚被定义）。
  - 设置 $y$ 和 $z$ 为 “活跃”（因为它们在这里用了）。
注意：上述步骤中，设置 $x$ 为不活跃和设置 $y$ 、 $z$ 为活跃的顺序（即后两步顺序）非常重要，因为 $x, y, z$ 可能会重复出现，如 $x=x+y$ 。

实际上为了跨基本块进行活跃变量分析，应当使用下节课的数据流分析去递归调用。

寄存器分配

getReg 函数

目标：减少 LD 和 ST 的指令数目。

任务：对一条指令 $x = y \; \text{op} \; z$ ，为运算分量 $y$ 和 $z$ 以及结果 $x$ 选择寄存器。

给运算分量选择寄存器：

如果已经在寄存器中，则选择该寄存器。
否则，如果有空闲寄存器，则选择一个空闲寄存器。
否则，设 $R$ $R$ 是一个候选寄存器，其存放了 $v$ $v$ 的值：
- 如果 $v$ 的地址描述符包含其它位置，则可以用 $R$ （还有别的地方存了，可以覆盖）。
- 如果 $v$ 就是 $x$ 且不为运算分量，则可以用 $R$ （ $x$ 是结果，本就要覆盖）。
- 如果 $v$ 在该语句后不是活跃变量，则可以用 $R$ （ $v$ 不会再用到，可以覆盖）。
否则，进行溢出操作（spill）。

溢出操作（spill）

设 $R$ 是候选寄存器，它存放了变量 $v$ 的值：

生成指令 $\text{ST} \; v, R$ ，并更新 $v$ 的地址描述符（把寄存器的值驱逐到内存中去）。
如果 $R$ 中还存放了别的变量的值，则可能要生成多条 ST 指令。
然后，我们就可以使用 $R$ 了。

寄存器的分配与指派

分配：哪些值应该放在寄存器中

指派：各个值应该存放在哪个寄存器

两个不同时活跃的变量可以使用同一个寄存器。

寄存器冲突图

构造寄存器冲突图（register-interference graph）

结点：在第一趟代码生成中使用的符号寄存器
边：两个符号寄存器不能指派同一个物理寄存器（相互冲突）则用边连起来

构造方法：

先假设寄存器无限，构造一次
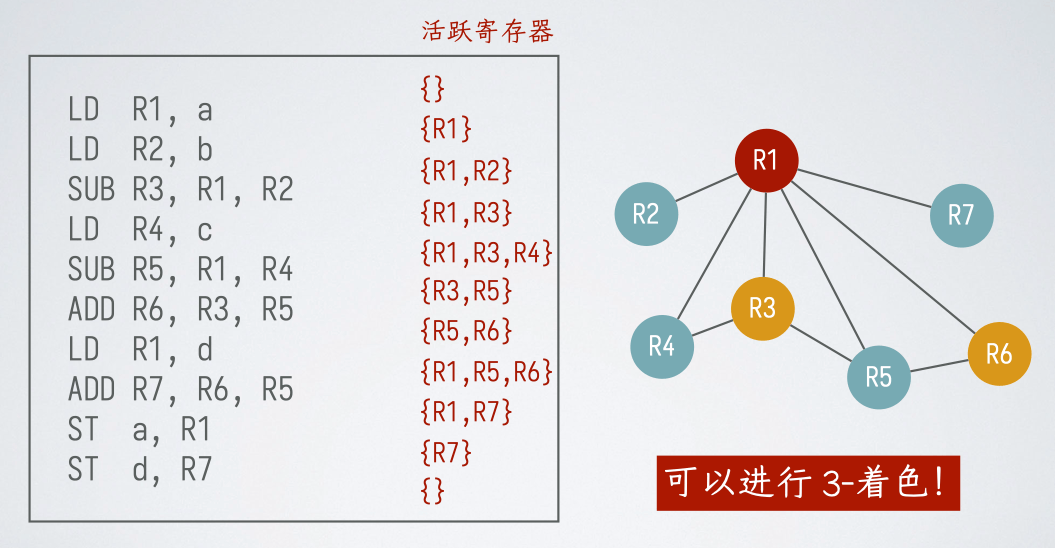
然后写出汇编代码，列出每步的活跃寄存器
将同时活跃的寄存器连线，构造出图染色问题，进行图着色后，相同颜色的结点可以分配同一个物理寄存器
如果最小能进行 n - 染色，则 n 个寄存器即可
如果不能进行 n - 染色，则需要增加寄存器或者进行溢出操作

冲突： $R_1$ 在 $R_2$ 被定值的地方是活跃的，也就是说如果存在在一个指令 $i$ ，使得 $\text{def}(i, R_2)$ 且 $\text{live}_\text{out}(i, R_1)$ ，这个时候我们不能将他们合并为一个寄存器，因为这两个值后续都要用。

62805

图着色算法的启发式技术

定理：如果冲突图中每个结点的度数都 $< m$ ，则总是可以 $m$ - 着色。

原因：每个结点邻居的颜色最多 $m - 1$ 种，总能对其着色。

算法

寻找度数 $< m$ 的结点，从图中删除，并把该结点压到一个栈中
如果所有结点的度数都 $\geq m$ $\geq m$ ：
- 找到一个溢出结点，不对它着色。
- 删除该结点。
当图为空的时候：
- 从栈顶依次弹出结点。
- 选择该结点的邻居没有使用的颜色进行着色。

如果有溢出：

为溢出结点生成代码，使用时加载到新的符号寄存器中
然后对新的代码重新进行活跃性分析和寄存器分配（反正大不了退化到一用一存，肯定能搞定）

溢出节点选择：降低溢出代价，即降低引入的额外指令的运行时开销，尤其是避免在循环中引入新代码。

拆分

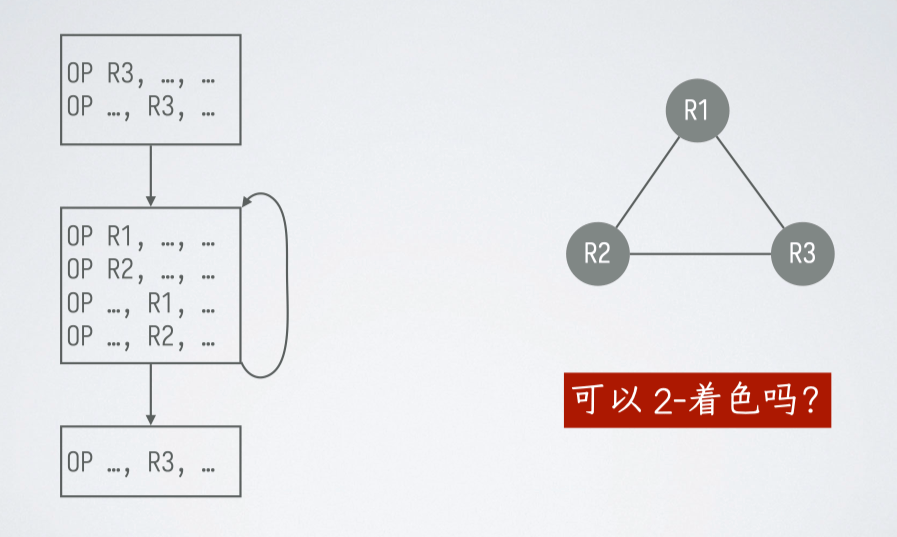
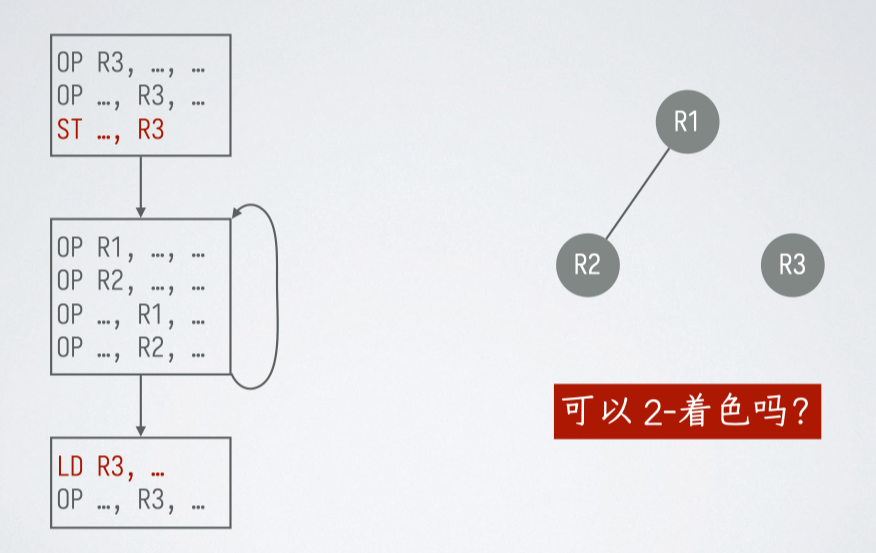
定义：对一个节点的 活跃范围 进行拆分，从而降低其在冲突图中的度数

把某个结点对应寄存器的值保存到内存中（故意加一句 $\text{ST} \; x, R_1$ ）
在拆分的地方把值再加载回来

16928

24486

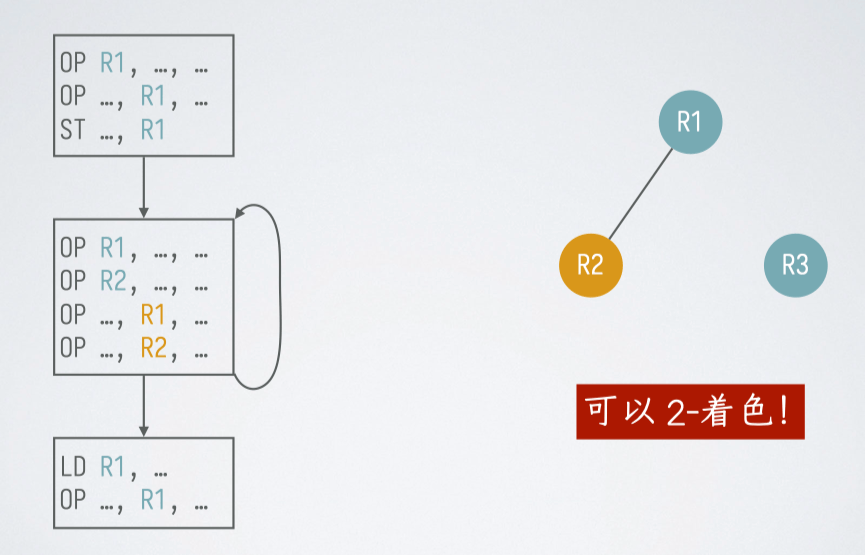
52353

合并

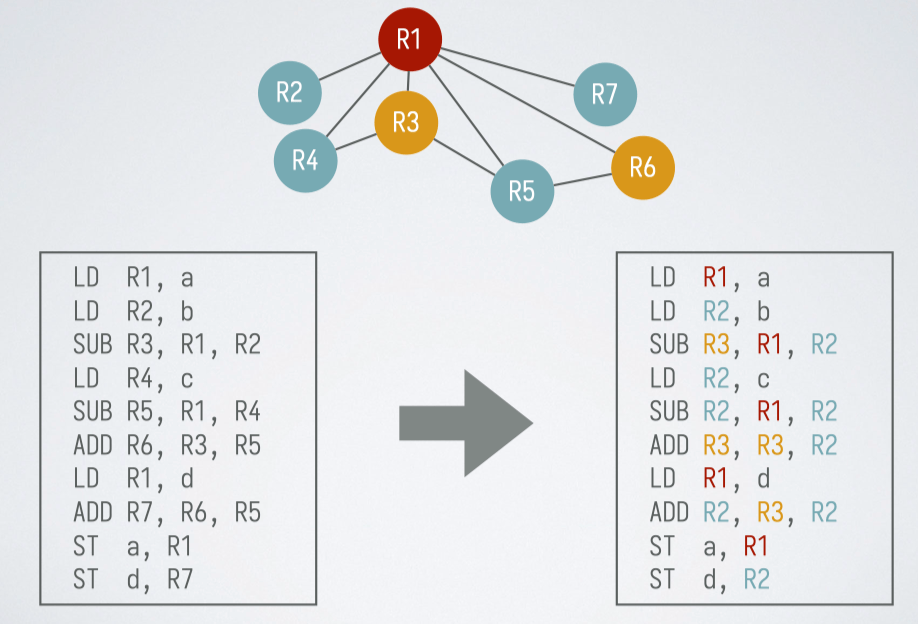
定义：如果 $R_1$ 和 $R_2$ 在冲突图中不相邻的话，那么就可以把它们合并（coalesce）成一个符号寄存器

75926

生成代码时，有大量的寄存器之间的拷贝，如 $\text{LD} \; R_1, R_2$
如果把 $R_1$ 和 $R_2$ 分配到同一个物理寄存器，就不需要执行该拷贝

问题：可能增加冲突边的数目，从而无法着色

解决方案 1：合并时不要创建高度数（ $\geq m$ ）的结点
解决方案 2：如果 $a$ $a$ 的每个邻居 $r$ $r$ 都满足下面的条件之一，才可以把 $a$ $a$ 与 $b$ $b$ 合并：
- $r$ 与 $b$ 之间有冲突
- $r$ 的度数比较低（ $< m$ ）

预着色

有些指令有默认寄存器，不可更改
当成特殊符号寄存器，在着色前就加入图中并染色
不要在这些节点溢出