马尔科夫决策过程(Markov Decision Process, MDP)#
状态集合 : S S S 动作集合 : A A A 状态转移函数 :P : ⟨ S , A , S ′ ⟩ → R + P: \langle S, A, S' \rangle \rightarrow \mathbb{R}^+ P : ⟨ S , A , S ′ ⟩ → R +
P ( s ′ ∣ s , a ) P(s'|s, a) P ( s ′ ∣ s , a ) s s s a a a s ′ s' s ′ 概率
奖励函数 :R : ⟨ S , A , R + ⟩ → R + R: \langle S, A, \mathbb{R}^+ \rangle \rightarrow \mathbb{R}^+ R : ⟨ S , A , R + ⟩ → R +
R ( s , a , r ) R(s, a, r) R ( s , a , r ) s s s a a a r r r 概率
马尔可夫性质 :在当前状态 S t S_t S t 状态转移模型 P P P R R R S t S_t S t ,和之前的状态及动作无关,也即:
P ( S t + 1 ∣ S t , A t , S t − 1 , A t − 1 , … , S 0 , A 0 ) = P ( S t + 1 ∣ S t , A t ) P(S_{t+1} \mid S_t, A_t, S_{t-1}, A_{t-1}, \ldots, S_0, A_0) = P(S_{t+1} \mid S_t, A_t) P ( S t + 1 ∣ S t , A t , S t − 1 , A t − 1 , … , S 0 , A 0 ) = P ( S t + 1 ∣ S t , A t ) 这条性质可以有力地简化问题。
有限 MDP:状态集合 S S S A A A
回顾定义#
首先,回顾一下上节课讲过的三个公式。
累积收益值 G t G_t G t #
表示从时间步 t t t
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = ∑ k = 0 ∞ γ k R t + k + 1 G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ = k = 0 ∑ ∞ γ k R t + k + 1 其中,γ \gamma γ 0 ≤ γ ≤ 1 0 \leq \gamma \leq 1 0 ≤ γ ≤ 1 R t R_t R t t t t 近期 的信息,忽略无限远的信息,保证了这个累积收益是 有界 的,不会是正无穷。从而使得策略是可比的。
注意在这个表达式中,越靠右的项,时序关系上越晚、越远(越靠近未来)
状态价值函数 V π ( s ) V_\pi(s) V π ( s ) #
表示在策略 π \pi π s s s
V π ( s ) = E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ R t + 2 + ⋯ ∣ S t = s ] V_\pi(s) = \mathbb{E}_\pi[G_t \mid S_t = s] = \mathbb{E}_\pi[R_{t+1} + \gamma R_{t+2} + \cdots \mid S_t = s] V π ( s ) = E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ R t + 2 + ⋯ ∣ S t = s ] 动作价值函数 Q π ( s , a ) Q_\pi(s, a) Q π ( s , a ) #
表示在策略 π \pi π s s s a a a
Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ R t + 1 + γ R t + 2 + ⋯ ∣ S t = s , A t = a ] Q_\pi(s, a) = \mathbb{E}_\pi[G_t \mid S_t = s, A_t = a] = \mathbb{E}_\pi[R_{t+1} + \gamma R_{t+2} + \cdots \mid S_t = s, A_t = a] Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] = E π [ R t + 1 + γ R t + 2 + ⋯ ∣ S t = s , A t = a ] Bellman 期望方程#
可以看到,在上述的三个函数中,计算某一状态、某一动作的价值时,没有显式地出现诸如 t − 1 t-1 t − 1 因为在计算期望时,并没有显式地提及状态转移的概率。
为此,我们引入 Bellman 期望方程,它是一个递归方程,可以用来计算状态价值函数和动作价值函数。
状态价值函数 V π ( s ) V_\pi(s) V π ( s ) #
表示在策略 π \pi π s s s
V π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] V_\pi(s) = \sum_a \pi(a|s) \sum_{s', r} p(s', r | s, a) [r + \gamma V_\pi(s')] V π ( s ) = a ∑ π ( a ∣ s ) s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ )]
π ( a ∣ s ) \pi(a|s) π ( a ∣ s ) s s s a a a p ( s ′ , r ∣ s , a ) p(s', r | s, a) p ( s ′ , r ∣ s , a ) s s s a a a s ′ s' s ′ r r r γ \gamma γ
动作价值函数 Q π ( s , a ) Q_\pi(s, a) Q π ( s , a ) #
表示在策略 π \pi π s s s a a a
Q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] Q_\pi(s, a) = \sum_{s', r} p(s', r | s, a) [r + \gamma V_\pi(s')] Q π ( s , a ) = s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ )] 同样的,p ( s ′ , r ∣ s , a ) p(s', r | s, a) p ( s ′ , r ∣ s , a ) s s s a a a s ′ s' s ′ r r r
状态价值函数与动作价值函数的关系#
状态价值函数可以通过动作价值函数表示:
V π ( s ) = ∑ a π ( a ∣ s ) Q π ( s , a ) V_\pi(s) = \sum_a \pi(a | s) Q_\pi(s, a) V π ( s ) = a ∑ π ( a ∣ s ) Q π ( s , a ) 即在状态 s s s s s s
这些式子指出一个特点:所有的转移概率 p ( s ′ , r ∣ s , a ) p(s', r | s, a) p ( s ′ , r ∣ s , a ) π ( a ∣ s ) \pi(a|s) π ( a ∣ s ) s s s a a a 这就是马尔可夫性质,即未来状态和奖励只依赖于当前的状态和动作 。
状态价值和最优策略#
最优状态价值 V ∗ ( s ) V^*(s) V ∗ ( s ) π \pi π 状态价值
V ∗ ( s ) = max π V π ( s ) V^*(s) = \max_{\pi} V_\pi(s) V ∗ ( s ) = π max V π ( s ) 最优策略 π ∗ \pi^* π ∗ s s s
状态价值只有一个,但是最优策略可以有多个纯策略或者最优纯策略的任意组合。
可以通过反证证明,任意一个最优策略,其对于整个状态空间中任意一个状态都是最优的。
动作价值和最优策略#
最优动作价值 Q ∗ ( s , a ) Q^*(s, a) Q ∗ ( s , a ) π \pi π 动作价值
Q ∗ ( s , a ) = max π Q π ( s , a ) Q^*(s, a) = \max_{\pi} Q_\pi(s, a) Q ∗ ( s , a ) = π max Q π ( s , a ) 最优策略 π ∗ \pi^* π ∗ s s s a a a
动作价值也只有一个,但是最优策略可以有多个纯策略或者最优纯策略的任意组合。
可以证明,任意一个最优策略,其对于整个状态空间中任意一个状态和动作的组合都是最优的,也即 全局最优解一定也是局部最优解 ,这正是马尔科夫性质的体现,这显著简化了计算复杂度,我们不需要考虑全局的状态,而只需要考虑多次局部状态即可。
Bellman 最优方程#
最优价值函数 V ∗ ( s ) V^*(s) V ∗ ( s ) Q ∗ ( s , a ) Q^*(s, a) Q ∗ ( s , a )
V ∗ ( s ) = max π V π ( s ) V^*(s) = \max_{\pi} V_{\pi}(s) V ∗ ( s ) = π max V π ( s ) Q ∗ ( s , a ) = max π Q π ( s , a ) Q^*(s, a) = \max_{\pi} Q_{\pi}(s, a) Q ∗ ( s , a ) = π max Q π ( s , a ) 由此可得:
V ∗ ( s ) = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ∗ ( s ′ ) ] = max a Q ∗ ( s , a ) V^*(s) = \max_{a} \sum_{s', r} p(s', r | s, a) [r + \gamma V^*(s')] = \max_a Q^*(s, a) V ∗ ( s ) = a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ V ∗ ( s ′ )] = a max Q ∗ ( s , a ) Q ∗ ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ max a ′ Q ∗ ( s ′ , a ′ ) ] Q^*(s, a) = \sum_{s', r} p(s', r | s, a) [r + \gamma \max_{a'} Q^*(s', a')] Q ∗ ( s , a ) = s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ a ′ max Q ∗ ( s ′ , a ′ )] 这两个式子暗含了动作价值 / 状态价值的唯一性,这是迭代 / 递归关系的基础。
用动态规划方法求解最优策略#
这对应状态转移函数和奖励函数 P , R P,R P , R 环境已知 。
动态规划理论#
多阶段决策过程
物理系统的 状态(state) 用一组状态变量描述。
决策(decisions) 引起状态变量的 转换(transformations) 。各个阶段的决策与状态转换,在阶段间是独立的,但是整个过程的目标是 最大化最终状态参数 的相关函数。
无后效性
考虑一个中间状态,决策时不关心之前的状态转换过程,只从当前状态出发。
这种特性称为 无后效性 。
最优原则
最优策略的性质:无论初始状态和最初的几个决策是什么,剩余决策一定构成一个与之前决策产生的状态相关的最优策略。
形式化描述:策略 π ( a ∣ s ) \pi(a|s) π ( a ∣ s ) s s s v π ( s ) = v ∗ ( s ) v_{\pi}(s) = v^*(s) v π ( s ) = v ∗ ( s ) s s s s ′ s' s ′ π \pi π s ′ s' s ′ v π ( s ′ ) = v ∗ ( s ′ ) v_{\pi}(s') = v^*(s') v π ( s ′ ) = v ∗ ( s ′ )
考虑在这个三角形中找到一个从顶部到底部某一节点的路径,使得经过的节点和最大。
如果不限定各层之间的关联,那么是无后效性的
如果限定下一层只能在上一层直接相连(最近)的左右子节点中选,那么是有后效性的,譬如第二次选了 8,那么第三层就只能选择 1 或者 0,这相比第二层选了 3 第三次选 8 是更劣的。
单源最短路径问题 Bellman-Ford 算法#
问题定义
给定一个带权有向图 G = ( V , E ) G=(V, E) G = ( V , E )
计算从源点(起点)到其他所有顶点的最短路径长度,称为单源最短路径问题。
算法步骤
初始化:源点距离设为 0,其他顶点距离设为 ∞ \infty ∞
进行 n − 1 n-1 n − 1 ( u , v ) ∈ E (u, v) \in E ( u , v ) ∈ E D i s t a n c e ( v ) Distance(v) D i s t an ce ( v ) n − 1 n-1 n − 1
检查是否存在负权环,如果存在则返回负权环信息。
策略估值 (Policy Evaluation)#
策略估值:对于任意策略 π \pi π V π V_\pi V π
策略估值的 Bellman 方程#
准确稳定 的状态值函数:
v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] v_\pi(s) = \sum_{a} \pi(a|s) \sum_{s',r} p(s', r | s, a) [r + \gamma v_\pi(s')] v π ( s ) = a ∑ π ( a ∣ s ) s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ )] 但是这个式子是迭代嵌套 v π v_\pi v π
迭代更新规则#
v k + 1 ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] v_{k+1}(s) = \sum_{a} \pi(a|s) \sum_{s',r} p(s', r | s, a) [r + \gamma v_k(s')] v k + 1 ( s ) = a ∑ π ( a ∣ s ) s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ )] 其中:
v k ( s ′ ) v_{k}(s') v k ( s ′ ) k k k s ′ s' s ′ v k + 1 ( s ) v_{k+1}(s) v k + 1 ( s ) k + 1 k+1 k + 1 s s s 状态 s ′ s' s ′ s s s
这个式子是 不准确 的,因为我们无法保证 v k ( s ′ ) = v π ( s ′ ) v_{k}(s') = v_\pi(s') v k ( s ′ ) = v π ( s ′ ) k k k
迭代策略估值 (Iterative Policy Evaluation)#
完全回溯(Full Backup)
根据被评估策略 π \pi π v k ( s ) v_k(s) v k ( s ) v k + 1 ( s ) , ∀ s ∈ S v_{k+1}(s), \forall s \in S v k + 1 ( s ) , ∀ s ∈ S
迭代停止条件
测试 max s ∈ S ∣ v k + 1 ( s ) − v k ( s ) ∣ \max_{s \in S} |v_{k+1}(s) - v_k(s)| max s ∈ S ∣ v k + 1 ( s ) − v k ( s ) ∣ v π v_\pi v π
迭代内循环计算
同步迭代(Synchronous Iteration)
异步迭代(Asynchronous Iteration)
同步迭代(Synchronous Iteration)#
计算过程:
已有 v k ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n ) v_k(s_1), v_k(s_2), \cdots, v_k(s_n) v k ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n )
用上述值依次计算 v k + 1 ( s 1 ) , v k + 1 ( s 2 ) , ⋯ , v k + 1 ( s n ) v_{k+1}(s_1), v_{k+1}(s_2), \cdots, v_{k+1}(s_n) v k + 1 ( s 1 ) , v k + 1 ( s 2 ) , ⋯ , v k + 1 ( s n )
需要双数组分别存储旧值和新值。
异步迭代(Asynchronous Iteration)#
计算过程:
用 v k ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n ) v_k(s_1), v_k(s_2), \cdots, v_k(s_n) v k ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n ) v k + 1 ( s 1 ) v_{k+1}(s_1) v k + 1 ( s 1 )
用 v k + 1 ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n ) v_{k+1}(s_1), v_k(s_2), \cdots, v_k(s_n) v k + 1 ( s 1 ) , v k ( s 2 ) , ⋯ , v k ( s n ) v k + 1 ( s 2 ) v_{k+1}(s_2) v k + 1 ( s 2 )
用 v k + 1 ( s 1 ) , v k + 1 ( s 2 ) , ⋯ , v k ( s n ) v_{k+1}(s_1), v_{k+1}(s_2), \cdots, v_k(s_n) v k + 1 ( s 1 ) , v k + 1 ( s 2 ) , ⋯ , v k ( s n ) v k + 1 ( s 3 ) v_{k+1}(s_3) v k + 1 ( s 3 )
只需 单数组 原位更新,可以更快地收敛。
伪代码#
Input π , the policy to be evaluated Initialize an array V ( s ) = 0 , for all s ∈ S Repeat Δ ← 0 For each s ∈ S : v ← V ( s ) V ( s ) ← ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ (a small positive number) Output V ≈ v π \begin{aligned}
&\text{Input }\pi,\text{the policy to be evaluated}\\
&\text{Initialize an array }V(s)=0,\text{for all }s\in\mathcal{S}\\
&\text{Repeat}\\
&\quad\Delta\leftarrow0\\
&\quad\text{For each }s\in\mathcal{S}{:}\\
&\quad\quad v\leftarrow V(s)\\
&\quad\quad V(s)\leftarrow\sum_{a}\pi(a|s)\sum_{s^{\prime},r}p(s^{\prime},r|s,a)\big[r+\gamma V(s^{\prime})\big]\\
&\quad\quad\Delta\leftarrow\max(\Delta,|v-V(s)|)\\&\text{until }\Delta<\theta\text{ (a small positive number)}\\&\text{Output }V\approx v_{\pi}\end{aligned} Input π , the policy to be evaluated Initialize an array V ( s ) = 0 , for all s ∈ S Repeat Δ ← 0 For each s ∈ S : v ← V ( s ) V ( s ) ← a ∑ π ( a ∣ s ) s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γV ( s ′ ) ] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ (a small positive number) Output V ≈ v π
输入策略 π \pi π :输入一个策略 π \pi π s s s a a a
初始化 :初始化一个值函数数组 V ( s ) V(s) V ( s ) s s s
迭代计算
设置一个变量 Δ \Delta Δ
对于每一个状态 s s s
保存当前状态 s s s V ( s ) V(s) V ( s ) v v v
使用策略 π \pi π p ( s ′ , r ∣ s , a ) p(s', r|s, a) p ( s ′ , r ∣ s , a ) s s s V ( s ) V(s) V ( s ) V ( s ) ← ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] V(s) \leftarrow \sum_{a} \pi(a|s) \sum_{s', r} p(s', r|s, a) [r + \gamma V(s')] V ( s ) ← ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γV ( s ′ )]
更新 Δ \Delta Δ V ( s ) V(s) V ( s ) v v v Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) \Delta \leftarrow \max(\Delta, |v - V(s)|) Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) Δ \Delta Δ
终止条件 :当 Δ \Delta Δ θ \theta θ
输出 :输出收敛后的值函数 V V V π \pi π v π v_\pi v π
v π v_\pi v π # 满足下述条件之一:
γ < 1 \gamma < 1 γ < 1 γ = 1 \gamma=1 γ = 1 v π v_\pi v π
依据策略 π \pi π
这意味着不会有无穷长的路径存在,无论初始状态是什么,对弈都会在有限步内结束,这保证了未来的奖励是有限的。
如果策略 π \pi π 。一个例子是 Bellman-Ford 算法,由于一条最长无环路径不会超过 n − 1 n-1 n − 1
迭代策略估值#
收敛性条件 :在上述存在性和唯一性保障条件下,迭代策略估值是收敛的。
值函数序列收敛 :随着迭代次数 k k k { V k } \{V_k\} { V k } V k → v π V_k \to v_\pi V k → v π 稳定的值函数 :即使迭代了很多次,也能得到一个稳定的关于策略 π \pi π v π v_\pi v π
策略提升(Policy Improvement)#
策略提升 :在原策略基础上,根据原策略计算得到的值函数,贪心地选择动作使得新策略的估值优于原策略,或者一样好。
先前讲的策略估值从未改变过策略本身,它只是在更新策略的状态价值表。而 策略提升会更新策略。
计算动作价值#
可以根据状态价值计算动作价值:
q π ( s , a ) = ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] q_{\pi}(s, a) = \sum_{s', r} p(s', r | s, a) [r + \gamma v_{\pi}(s')] q π ( s , a ) = s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ )] 产生新策略#
贪心选择动作产生新策略:
π ′ ( s ) = arg max a q π ( s , a ) \pi'(s) = \arg\max_{a} q_{\pi}(s, a) π ′ ( s ) = arg a max q π ( s , a ) 即:
π ′ ( s ) = arg max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] \pi'(s) = \arg\max_{a} \sum_{s', r} p(s', r | s, a) [r + \gamma v_{\pi}(s')] π ′ ( s ) = arg a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ )] 策略提升总结#
在某个状态 s s s π \pi π q π q_\pi q π q π ′ q_{\pi'} q π ′ s s s π \pi π π ′ \pi' π ′
因为其他状态的动作都保持不变,对于所有状态 s s s V π ′ ( s ) = ∑ a π ′ ( a ∣ s ) Q π ′ ( s , a ) V_{\pi'}(s) = \sum_a \pi'(a | s) Q_{\pi'}(s, a) V π ′ ( s ) = ∑ a π ′ ( a ∣ s ) Q π ′ ( s , a ) V π ( s ) V_{\pi}(s) V π ( s )
一个很容易想到的策略提升是,在所有 s s s q q q
如果有多个 q q q q q q
策略提升后,状态价值对新策略估计的就不准确了,需要重新估计 v π ′ v_{\pi'} v π ′
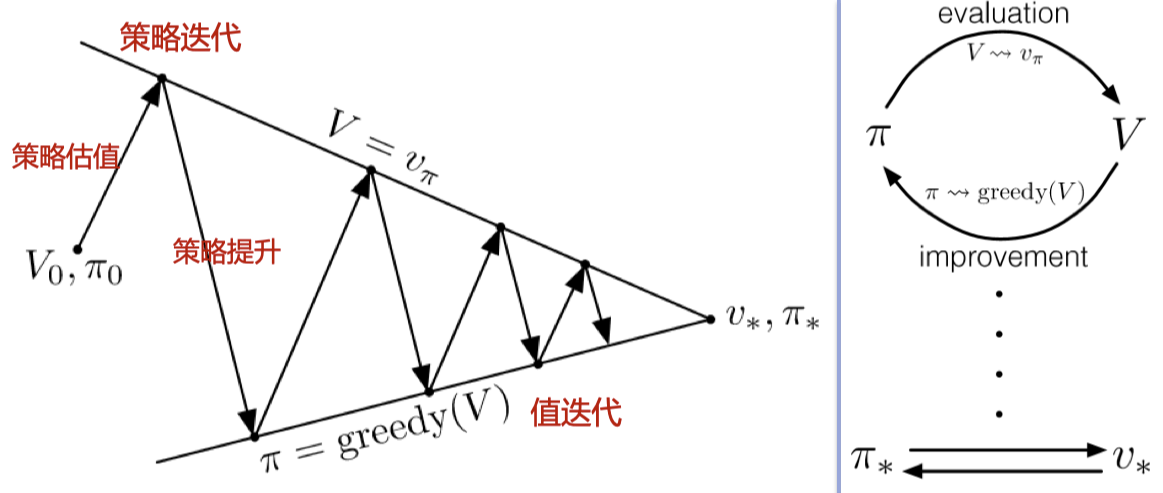
策略迭代#
策略迭代 :交替进行迭代策略估值和策略提升,在有限步之后找到最优策略与最优值函数。
π 0 → E v π 0 → I π 1 → E v π 1 → I π 2 → E ⋯ → I π ∗ → E v ∗ \pi_0 \xrightarrow{E} v_{\pi_0} \xrightarrow{I} \pi_1 \xrightarrow{E} v_{\pi_1} \xrightarrow{I} \pi_2 \xrightarrow{E} \cdots \xrightarrow{I} \pi^* \xrightarrow{E} v^* π 0 E v π 0 I π 1 E v π 1 I π 2 E ⋯ I π ∗ E v ∗ 其中,→ E \xrightarrow{E} E → I \xrightarrow{I} I
以上交替进行会得到策略序列 { π } \{\pi\} { π }
伪代码#
初始化
V ( s ) ∈ R and π ( s ) ∈ A ( s ) arbitrarily for all s ∈ S V(s) \in \mathbb{R} \text{ and } \pi(s) \in \mathcal{A}(s) \text{ arbitrarily for all } s \in \mathcal{S} V ( s ) ∈ R and π ( s ) ∈ A ( s ) arbitrarily for all s ∈ S
策略估值
Repeat Δ ← 0 For each s ∈ S : v ← V ( s ) V ( s ) ← ∑ s ′ , r p ( s ′ , r ∣ s , π ( s ) ) [ r + γ V ( s ′ ) ] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ (a small positive number) \begin{aligned}
&\text{Repeat}\\
&\quad \Delta \leftarrow 0\\
&\quad \text{For each } s \in \mathcal{S}:\\
&\quad\quad v \leftarrow V(s)\\
&\quad\quad V(s) \leftarrow \sum_{s', r} p(s', r | s, \pi(s)) [r + \gamma V(s')]\\
&\quad\quad \Delta \leftarrow \max(\Delta, |v - V(s)|)\\
&\text{until } \Delta < \theta \text{ (a small positive number)}
\end{aligned} Repeat Δ ← 0 For each s ∈ S : v ← V ( s ) V ( s ) ← s ′ , r ∑ p ( s ′ , r ∣ s , π ( s )) [ r + γV ( s ′ )] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ (a small positive number)
策略提升
policy-stable ← True For each s ∈ S : old-action ← π ( s ) π ( s ) ← arg max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] If old-action ≠ π ( s ) , then policy-stable ← False If policy-stable, then stop and return V ≈ v ∗ and π ≈ π ∗ ; else go to 2 \begin{aligned}
&\text{policy-stable} \leftarrow \text{True}\\
&\text{For each } s \in \mathcal{S}:\\
&\quad \text{old-action} \leftarrow \pi(s)\\
&\quad \pi(s) \leftarrow \arg\max_a \sum_{s', r} p(s', r | s, a) [r + \gamma V(s')]\\
&\quad \text{If } \text{old-action} \ne \pi(s), \text{ then policy-stable} \leftarrow \text{False}\\
&\text{If policy-stable, then stop and return } V \approx v_* \text{ and } \pi \approx \pi_*; \text{ else go to 2}
\end{aligned} policy-stable ← True For each s ∈ S : old-action ← π ( s ) π ( s ) ← arg a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γV ( s ′ )] If old-action = π ( s ) , then policy-stable ← False If policy-stable, then stop and return V ≈ v ∗ and π ≈ π ∗ ; else go to 2
策略提升结束条件#
假设新策略 π ′ \pi' π ′ π \pi π v π = v π ′ v_{\pi} = v_{\pi'} v π = v π ′ s s s
v π ′ ( s ) = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ′ ( s ′ ) ] \begin{aligned}
v_{\pi'}(s) &= \max_a \sum_{s', r} p(s', r | s, a) [r + \gamma v_{\pi}(s')] \\
&= \max_a \sum_{s', r} p(s', r | s, a) [r + \gamma v_{\pi'}(s')]
\end{aligned} v π ′ ( s ) = a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ )] = a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v π ′ ( s ′ )] 与 Bellman 最优方程相同,因此 v π ′ v_{\pi'} v π ′ v ∗ v^* v ∗ π ′ \pi' π ′ π \pi π
值迭代(Value Iteration)#
策略迭代的问题#
策略估值耗费时间
随着策略估值、提升的多次迭代,在后面的迭代中,对于某些状态,依据策略选择的动作已经是最优的了,此时策略估值不再改变(最优意味着即使再经过策略提升后,其动作也不会改变,只会进一步更新估值),对策略提升都没有帮助
所以可以提前截断估值
自然地,我们想到一种极端的修正方式
只做一次估值,不需要估值收敛就开始策略提升
这就是 值迭代方法
v k + 1 ( s ) = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] v_{k+1}(s) = \max_a \sum_{s', r} p(s', r | s, a) \left[ r + \gamma v_k(s') \right] v k + 1 ( s ) = a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γ v k ( s ′ ) ] 在值迭代中,每次更新直接计算在状态 s s s a a a 期望 回报,并取其最大值作为新的状态值。这个过程 同时完成了值函数更新和策略提升 。与之相对的,在策略迭代中,评估和提升是两个独立的步骤。
策略迭代 :每次策略提升前需要完全评估当前策略,可能需要多次迭代(策略评估目的是计算策略估值表,计算过程是循环的,终止条件是估值稳定 / 收敛 ),计算开销较大值迭代 :每次迭代直接更新值函数,通常收敛速度更快。值迭代通常计算效率更高,因为它 减少了评估步骤的迭代次数
值迭代算法伪代码#
Algorithm parameter: a small threshold θ > 0 determining accuracy of estimation Initialize V ( s ) , for all s ∈ S + , arbitrarily except that V ( terminal ) = 0 Loop: Δ ← 0 Loop for each s ∈ S : v ← V ( s ) V ( s ) ← max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ Output a deterministic policy, π ≈ π ∗ , such that π ( s ) = arg max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] \begin{aligned}
&\text{Algorithm parameter: a small threshold } \theta > 0 \text{ determining accuracy of estimation} \\
&\text{Initialize } V(s), \text{ for all } s \in S^+, \text{ arbitrarily except that } V(\text{terminal}) = 0 \\
&\text{Loop:} \\
&\quad \Delta \leftarrow 0 \\
&\quad \text{Loop for each } s \in S: \\
&\quad\quad v \leftarrow V(s) \\
&\quad\quad V(s) \leftarrow \max_a \sum_{s', r} p(s', r | s, a) \left[ r + \gamma V(s') \right] \\
&\quad\quad \Delta \leftarrow \max(\Delta, |v - V(s)|) \\
&\text{until } \Delta < \theta \\
&\text{Output a deterministic policy, } \pi \approx \pi_*, \text{ such that } \\
&\quad \pi(s) = \arg\max_a \sum_{s', r} p(s', r | s, a) \left[ r + \gamma V(s') \right]
\end{aligned} Algorithm parameter: a small threshold θ > 0 determining accuracy of estimation Initialize V ( s ) , for all s ∈ S + , arbitrarily except that V ( terminal ) = 0 Loop: Δ ← 0 Loop for each s ∈ S : v ← V ( s ) V ( s ) ← a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γV ( s ′ ) ] Δ ← max ( Δ , ∣ v − V ( s ) ∣ ) until Δ < θ Output a deterministic policy, π ≈ π ∗ , such that π ( s ) = arg a max s ′ , r ∑ p ( s ′ , r ∣ s , a ) [ r + γV ( s ′ ) ]
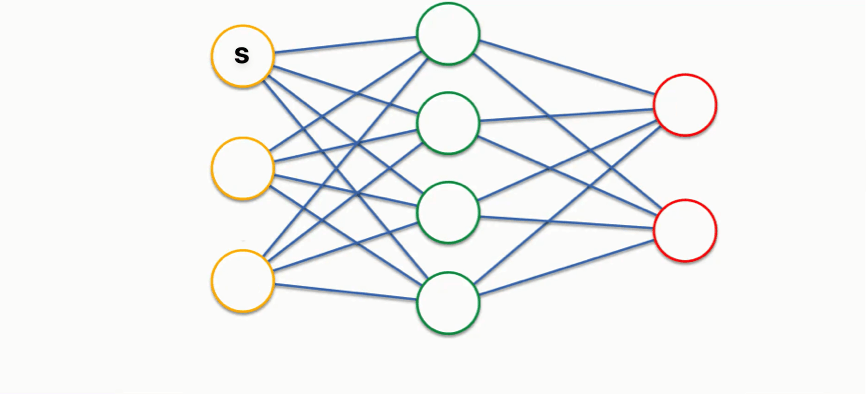
下面给出一个基于全连接层图示的、更为直观的理解:
考虑我们现有的一个状态 s s s
对于策略迭代中的策略提升,我们:
根据所有红色圆圈的估值,依据动作概率加权
更新所有的绿色圆圈的估值
根据更新后的绿色圆圈估值,依据动作概率加权
更新 s s s
那么,在两次策略评估的迭代之间,一旦任意一个绿色圆圈发生了改变,其势必影响到所有可以转移到他的、上游的黄色圆圈们,造成更新。这会导致策略评估的迭代次数很多。
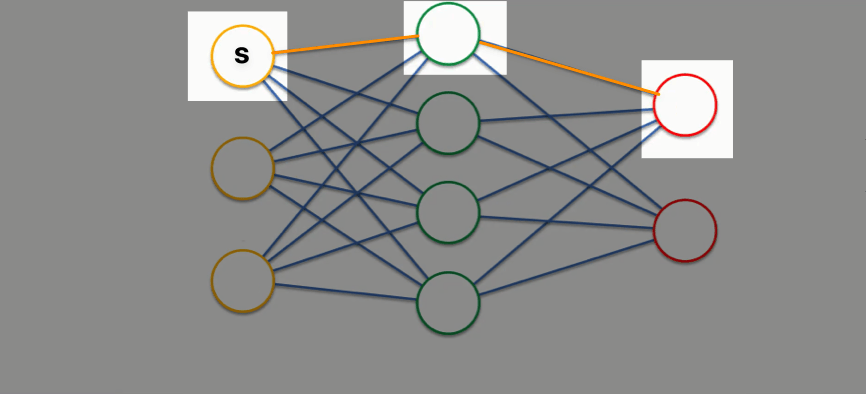
但是对于值迭代:
根据所有红色圆圈,选择最大的估值,直接更新绿色圆圈估值
根据更新后的绿色圆圈估值,选择最大的估值,直接更新 s s s
可以看到,由于选择了最大的估值,所以只要最大的估值对应的状态的估值没有发生改变,那么上游的黄色圆圈就不会变动估值,也就不会更新算法中指征收敛状态的 Δ \Delta Δ
值迭代算法的收敛性分析#
引理:压缩映射定理,一个压缩映射最多有一个不动点(压缩映射定理是闭区间套定理的直接推广)。
证明:
Δ = max s ∣ V i + 1 ( s ) − V i ( s ) ∣ = ∣ ∣ V i + 1 − V i ∣ ∣ 一轮值迭代中估值变化最大值, where ∣ ∣ V ∣ ∣ = max S ∣ V ( s ) ∣ \Delta = \max_s | V_{i+1}(s) - V_i(s) | = ||V_{i+1} - V_i|| \quad \text{一轮值迭代中估值变化最大值,}\\
\text{where }||V||=\max_S|V(s)| Δ = s max ∣ V i + 1 ( s ) − V i ( s ) ∣ = ∣∣ V i + 1 − V i ∣∣ 一轮值迭代中估值变化最大值, where ∣∣ V ∣∣ = S max ∣ V ( s ) ∣ V i + 1 ( s ) = max a ( R + γ V i ( s ′ ) ) V_{i+1}(s) = \max_a \left( R + \gamma V_i(s') \right) V i + 1 ( s ) = a max ( R + γ V i ( s ′ ) ) V i + 2 ( s ) ≤ max a ( R + γ V i ( s ′ ) + γ Δ ) V_{i+2}(s) \leq \max_a (R + \gamma V_i(s') + \gamma \Delta) V i + 2 ( s ) ≤ a max ( R + γ V i ( s ′ ) + γ Δ ) V i + 2 ( s ) − V i + 1 ( s ) ≤ max a ( R + γ V i ( s ′ ) + γ Δ ) − max a ( R + γ V i ( s ′ ) ) = γ Δ V_{i+2}(s) - V_{i+1}(s) \leq \max_a (R + \gamma V_i(s') + \gamma \Delta) - \max_a (R + \gamma V_i(s')) = \gamma \Delta V i + 2 ( s ) − V i + 1 ( s ) ≤ a max ( R + γ V i ( s ′ ) + γ Δ ) − a max ( R + γ V i ( s ′ )) = γ Δ 所以,
∣ ∣ B V i + 1 − B V i ∣ ∣ ≤ γ ∣ ∣ V i + 1 − V i ∣ ∣ where B V i + 1 ( s ) = max a ( R ( s , a ) + γ V i ( s ′ ) ) ||BV_{i+1} - BV_i|| \leq \gamma ||V_{i+1} - V_i||\\
\text{where }BV_{i+1}(s) = \max_a \left( R(s, a) + \gamma V_i(s') \right) ∣∣ B V i + 1 − B V i ∣∣ ≤ γ ∣∣ V i + 1 − V i ∣∣ where B V i + 1 ( s ) = a max ( R ( s , a ) + γ V i ( s ′ ) ) 所以值迭代算法(贝尔曼更新)是 压缩映射 ,从而其最多有一个不动点,也就是说,值迭代算法收敛。
广义策略迭代(Generalized Policy Iteration)#
用采样方法逼近最优策略#
这对应状态转移函数和奖励函数 P , R P,R P , R 环境 未知。
Bootstrap#
Bootstrap(自举) 是一种统计方法,用于估计样本的分布。它通过反复从原始数据集中 有放回地抽样 ,生成多个子样本,然后 计算这些子样本的统计量来估计总体的统计性质 。
在强化学习中,bootstrap 是指 计算一个状态的估值是依据它的后继状态的估值 。
蒙特卡洛学习#
蒙特卡洛学习方法用于强化学习中,它不需要环境的转移概率(P P P R R R
蒙特卡洛学习方法假设环境未知,不使用 bootstrap 。
蒙特卡洛方法通过多次模拟整个过程( 直到终止状态 ),然后利用实际获得的总回报来更新状态值。公式表示为:
V ( s ) = 1 N ∑ i = 1 N G i V(s) = \frac{1}{N} \sum_{i=1}^{N} G_i V ( s ) = N 1 i = 1 ∑ N G i 其中,G i G_i G i i i i N N N
没有复杂的状态转移关系、计算估值这种精确但是慢的很的玩意,就是硬尝试,至于准确性?交给大数定理。
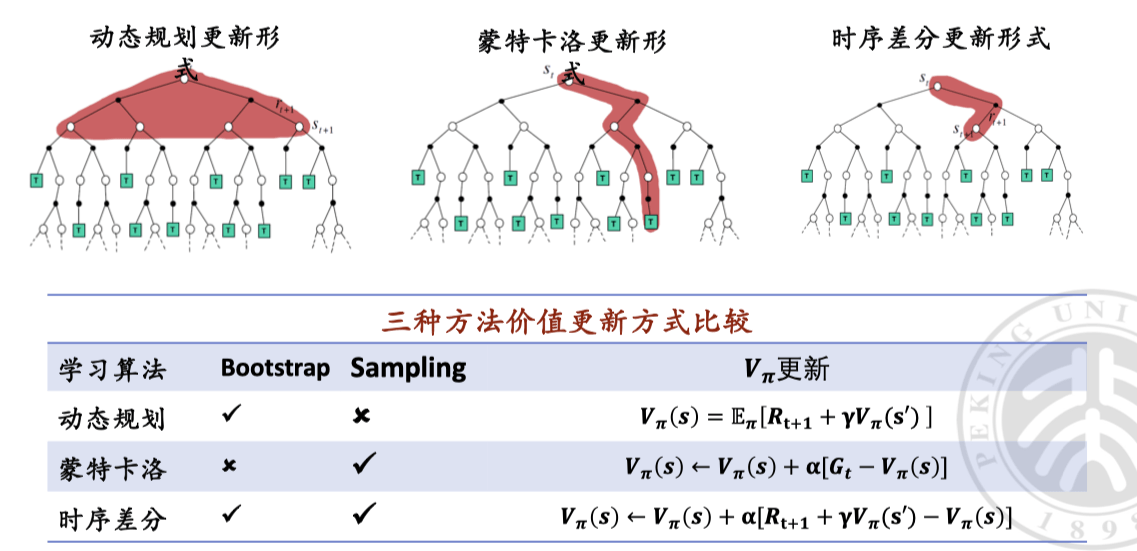
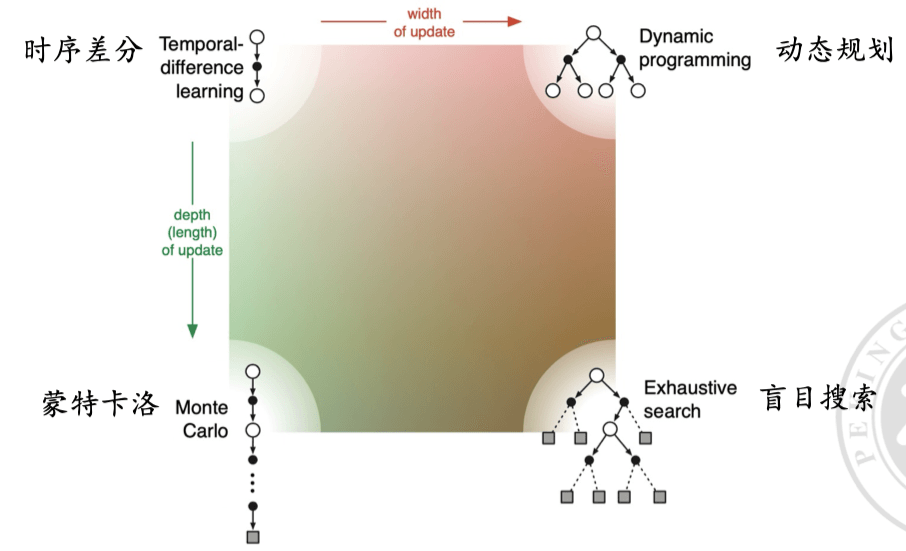
时序差分学习#
时序差分学习结合了动态规划和蒙特卡洛方法的优点,它依赖于后续状态的估值来更新当前状态的估值,但不需要知道环境的转移概率(P P P R R R
时序差分学习方法假设环境未知,但是使用 bootstrap 。
它通过每一步的估值误差来更新状态值,公式表示为:
V ( s ) ← V ( s ) + α [ R + γ V ( s ′ ) − V ( s ) ] V(s) \leftarrow V(s) + \alpha [R + \gamma V(s') - V(s)] V ( s ) ← V ( s ) + α [ R + γV ( s ′ ) − V ( s )] 其中,α \alpha α γ \gamma γ R R R V ( s ′ ) V(s') V ( s ′ )
下表重要,要记住。
Credit#
dadadaplz / 策略迭代与值迭代的区别 ↗