局部搜索和优化 • Arthals' ink

局部搜索算法

全局搜索回顾

全局搜索：从初始状态出发，遍历整个动作序列空间寻找目标状态。全局搜索需要记住搜索路径，受到内存限制，不适合解决超大规模问题。
无信息搜索：盲目遍历整个动作序列空间。
A*：使用问题相关的启发式函数加快搜索。

局部优化

为了快速解决 100+ 皇后问题，我们不再寻找全部解，而是 只找一个可行解。

我们不再关心得到解的路径（如，先摆第一个，再摆第二个…），只需要得到解（只要最后是解就行）。我们将启发式函数被改成状态估值函数，并充分利用它来寻找解。

全局搜索：对整个状态空间搜索，从初始状态开始（摆了零个）。利用摆皇后这个动作进行状态转移（动作确定路径），从摆了 $n$ 个变到摆了 $n+1$ 个

局部调整：先将八个皇后随意摆放到棋盘的八列上，然后调整被攻击的皇后，直到八个皇后互不攻击

八皇后问题重新建模

初始状态 $S_0$ ：八个皇后在棋盘上，每列有一个皇后。因为如果 8 个皇后不相互攻击，那么 8 个皇后肯定是在不同列的。
动作：移动任意列上的皇后到同列其他行（每个皇后有 7 个可能的动作，8 个皇后一共有 $8 \times 7 = 56$ 种可能动作）。
状态转移：移动后棋盘的样子（邻居状态，注意不再是父子状态，它们是并行关系，56 个）。
目标状态：皇后不互相攻击。
状态估值函数 $h$ ：互相攻击的皇后对的数目，表示当前状态的好坏。如果两个皇后可以相互攻击，则 $h$ 加 1。 $h(S)$ 以当前状态 $S$ 为输入，输出一个评估值。

优化目标

目标：使估值函数 $h$ 最小化，目标是 $h=0$ 。

策略：不断地将当前状态移动到邻居状态中估值更低（或者更高）的位置。直到到达目标状态。

优化过程

基本思路：从一个初始状态出发，不断地向更好的邻居状态移动

算法终止：当邻居状态中没有比当前状态更好的状态时（也即来到了 局部极值点 ），算法终止。

最优性条件：局部最优解不一定是全局最优解，但是局部最优解是全局最优解的一个 可能解。如果全局只有一个极值点，那么局部最优解就是全局最优解。

解空间的形状

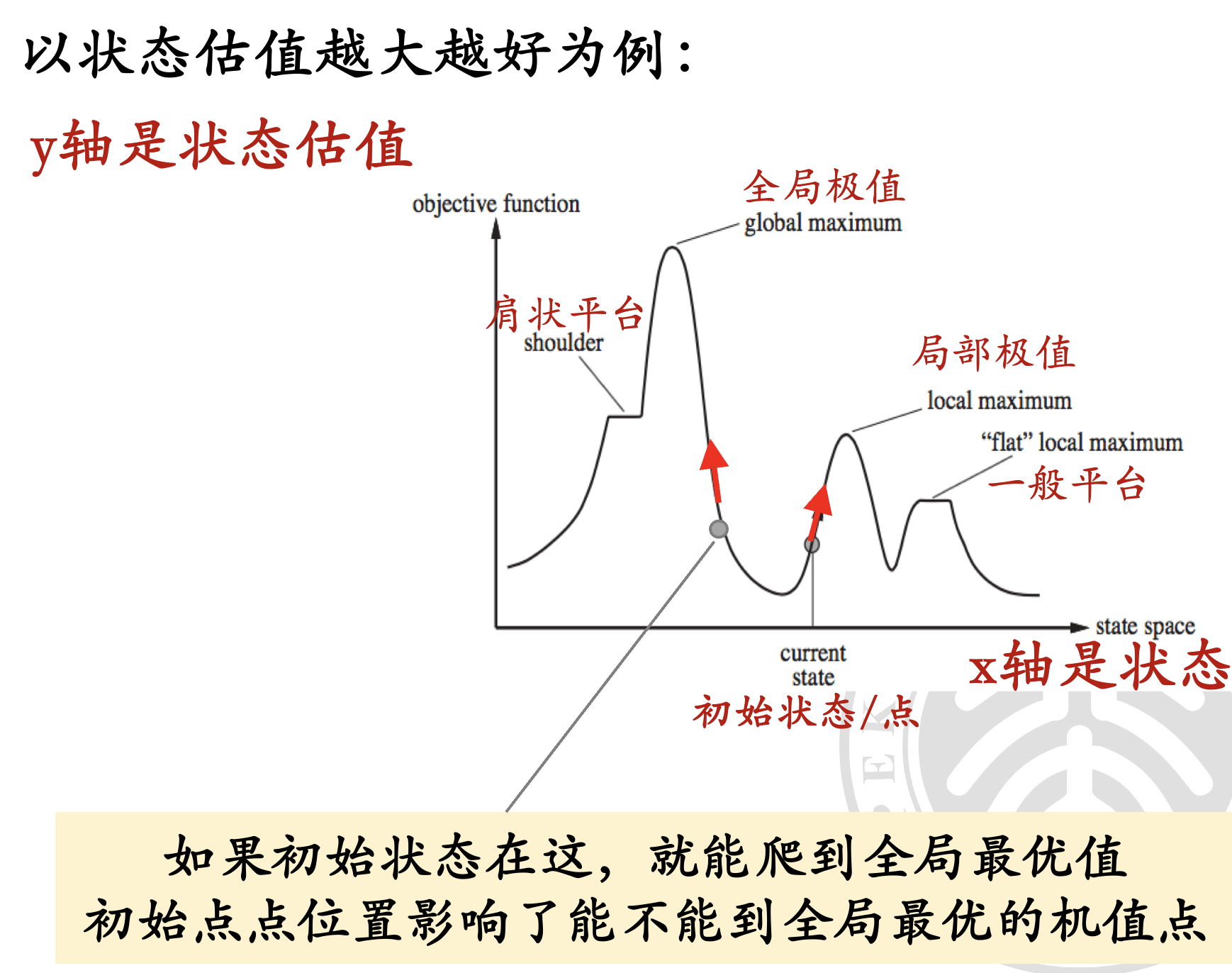
假设状态是一个连续变化的值，X 轴表示状态 $x$ ，Y 轴表示评估值 $f(x)$ 。对于一维的情况，评估值变化与各概念的关系如上图所示。

局部极值：某个区域内，某个点的评估值最高（或最低）。
多个局部极值点存在时，贪婪策略最终到达的极值点取决于 初始状态。
全局最优：全局最优解是所有局部最优解中评估值最高（或最低）的解。
平台：邻近状态评估值相同，无法决定移动方向。
肩状平台：一侧评估值可上升，另一侧下降。

实际情况中，状态的维度会更高（甚至无法可视化）。

解空间形状带来的问题

如何跳出局部极值点而奔向全局最优点？

进入平台时如何解决？

这些在后文都会有介绍。

局部优化算法的完备性和最优性

完备性：如果目标存在，则算法总能找到。
最优性：算法能找到全局最优解。

爬山法（Hill Climbing）

爬山法是一种局部搜索算法，主要用于求解优化问题。

以下是几个主要版本及其特点：

最陡下降爬山法（Steepest-Ascent Hill-Climbing）

算法

每次选择相邻节点中评估值 最优（这暗示最陡） 的一个，移动到该节点。
算法会在一个山峰（即四周点的评估值都比它低，局部最优值 ）处停止。
不存储搜索树，只存储 当前节点 和一个 估值函数。

伪代码

\begin{array}{l} \textbf{function} \ \text{HILL-CLIMBING}(problem) \ \textbf{returns} \ \text{a state that is a local maximum} \\ \quad \text{// 初始化当前节点为问题的初始状态} \\ \quad \text{current} \leftarrow \text{MAKE-NODE}(problem.\text{INITIAL-STATE}) \\ \quad \text{loop do} \\ \quad \quad \text{// 找到当前节点的最高值后继节点} \\ \quad \quad \text{neighbor} \leftarrow \text{a highest-valued successor of current} \\ \quad \quad \text{// 如果邻居节点的值不大于当前节点的值，则返回当前节点的状态} \\ \quad \quad \text{if neighbor.VALUE} \leq \text{current.VALUE then return current.STATE} \\ \quad \quad \text{// 更新当前节点为邻居节点} \\ \quad \quad \text{current} \leftarrow \text{neighbor} \\ \end{array}

将初始状态设置为当前状态。
循环：
- 找出当前状态下估值最大的邻居节点。
- 如果邻居节点的估值小于当前状态，则返回当前状态作为解（这代表当前状态是局部最优解）。
- 否则，将当前状态更新为邻居节点。

优点：内存开销小，只需要存储当前状态。

缺点：可能陷入 局部最优。

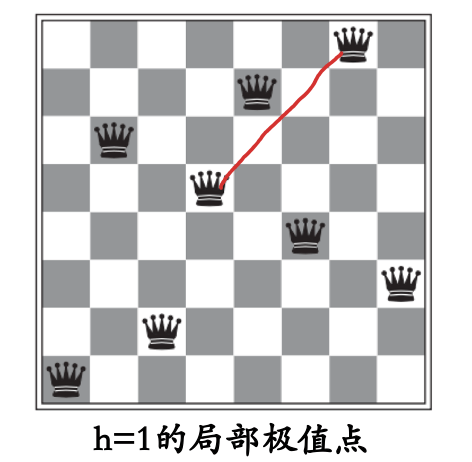
优化：随机平移

随机选择一个估值函数的值相同的邻居节点，尝试跳出局部最优。需要设置一个 移动次数上限，避免死循环。

只能跳出 肩状平台 （一侧），无法跳出整体平台。

随机爬山法（Stochastic Hill-Climbing）

算法

从更优的邻居点中 随机选择一个 进行移动，而 不是选择最优点 （那就是最陡爬山法了）。
比最陡下降爬山法 收敛慢，但在某些空间中 可能找到更优的解。
选择概率可以根据陡峭程度设定，以加速收敛。

第一选择爬山法（First-Choice Hill-Climbing）

过往缺陷

最陡爬山和随机爬山法都要计算所有邻居的估值，也即 生成估值表，当邻居很多的时候，需要的计算量很大。

第一选择爬山法通过每次只计算一个状态来避免此问题。

算法

随机选择一个邻居，如果它比当前状态好，就立即移动到邻居状态。否则，继续随机选择邻居，直到找到一个比当前状态好的邻居。
不需要生成估值表，每次只需要计算一个状态的估值。

随机重启爬山法（Random-Restart Hill-Climbing）

过往缺陷

之前的算法都是 不完备 的，因为可能陷入局部最优。

随机重启爬山法通过选择多个随机初始状态（类似暴力算法）来在一定程度上解决这个问题（没有完全解决），多次尝试寻找最优解，达到 近乎完备。

算法

找不到解时，从随机位置重新开始。
多次随机产生初始状态，接近完备，因为总会有一个初始状态能找到解（还有可能直接初始化到了解的位置（bushi））。

成功与否 取决于状态空间的形状，如果局部极值和平台不多，能快速找到好的解。

如果一次就找到最优解成功率是 $p$ ，那么期望的重启次数是 $1/p$ 。

模拟退火算法

过往问题

爬山法：只向更优邻居点移动，不会向状态估值更差的邻居移动，可能 陷入局部极值，因此是不完备的。
纯粹的随机游走算法
- 不使用 $h(n)$ 的搜索算法。
- 等概率地向任何一个邻居移动，是完备的，但却是 非常低效的。

从而，我们想到是否可以适当的结合两种算法，利用爬山法加快搜索，利用随机游走算法的随机性提高完备程度。

仿照物理中的退火，我们提出如下思想：

在搜索的初期以一个较大概率允许向下走
这个概率和这一步 “坏” 的程度成指数关系。
随着时间的推移这个概率会变小，这个概率会随着 “温度” 的下降而下降。

我们可以设法让 “温度” 足够慢地下降，此时算法会最终以接近 1 的概率找到全局最优解（因为这样会很接近随机游走算法）。

伪代码

\begin{array}{l} \textbf{function} \ \text{SIMULATED-ANNEALING}(problem, schedule) \ \textbf{returns} \ \text{a solution state} \\ \quad \text{// 输入: problem，一个问题} \\ \quad \text{// schedule，一个从时间到“温度”的映射} \\ \\ \quad \text{// 初始化当前节点为问题的初始状态} \\ \quad current \leftarrow \text{MAKE-NODE}(problem.\text{INITIAL-STATE}) \\ \quad \textbf{for} \ t = 1 \ \text{to} \ \infty \ \textbf{do} \\ \quad \quad \text{// 根据时间 t 计算当前温度} \\ \quad \quad T \leftarrow \text{schedule}(t) \\ \quad \quad \textbf{if} \ T = 0 \ \textbf{then return} \ current \\ \quad \quad \text{// 随机选择当前节点的一个后继节点} \\ \quad \quad next \leftarrow \text{a randomly selected successor of} \ current \\ \quad \quad \text{// 计算邻居状态和当前状态的估值差异} \\ \quad \quad \Delta E \leftarrow \text{next.VALUE} - \text{current.VALUE} \\ \quad \quad \text{// 如果邻居状态更好，直接跳到邻居状态} \\ \quad \quad \textbf{if} \ \Delta E > 0 \ \textbf{then} \ current \leftarrow next \\ \quad \quad \text{// 否则，以 $e^{\Delta E / T}$ 的概率接受新的节点} \\ \quad \quad \textbf{else} \ current \leftarrow next \ \text{only with probability} \ e^{\Delta E / T} \\ \end{array}

温度：表示为 $T$ ，随着时间 $t$ 的变化而变化。
ΔE：表示邻居状态值与当前状态值的差。
概率跳跃：以概率 $e^{\Delta E / T}$ 决定是否跳跃到新的邻居状态。
- $T$ 在指数分母上，随着时间增加跳跃概率越来越小。
- $\Delta E$ 在指数分子上，跳跃概率为随着 $\Delta E$ 的增加而增加。
  当 $\Delta E$ 为正时，直接跳跃到新的邻居状态。这对应邻居估值高于当前状态，跳过去是优化的。
  当 $\Delta E$ 为负时，跳跃概率为 $e^{\Delta E / T}$ ，跳跃概率随着温度的降低而降低。这对应跳过去是非优化的。这样看上去会更差，但是正是因为在非优化的情况下还有概率选择跳跃，所以模拟退火算法能够跳出局部最优，增加达到全局最优的可能。

超参数（Hyper-parameters）选择

初始温度（步幅）：应设定多大？
降温速率：以何种速率降低温度？
终止温度：温度降到什么程度可以报告解？

具体问题具体分析：根据具体问题调整超参数。

总结

初期允许以较大概率向下走，概率与 “坏” 的程度成指数关系。
随时间推移，概率变小，温度下降。

若温度足够慢地下降，算法会最终以 接近 1 的概率找到全局最优解。

对比

爬山法与模拟退火法对比：

爬山法：简单搜索法，可能陷入局部最优。
模拟退火：通过概率跳跃机制，有效跳出局部极值，寻找全局最优解。

内存开销：这两个算法都只记录当前节点（而不是像之前的全局搜索的搜索树一样记录很多的节点状态），内存不会随着时间增加。

不过，这也是缺点，因为没法很好的利用内存来加快搜索。

局部束搜索（Local Beam Search）

算法过程

从 $k$ 个随机生成的初始状态开始。
每一步，所有 $k$ 个状态各自生成后继，共有 $k \times b$ 个后继。
若 $k \times b$ 个后继中有一个是全局最优点，则算法结束。否则，从 $k \times b$ 个后继中找出 $k$ 个最好的后继作为新状态，继续算法。

比较

局部束算法不同于同时运行的多个随机重启爬山法。

同时运行的多个随机重启爬山法：各搜索独立进行，不通讯。
局部束搜索：第 3 步中选择最优的 $k$ 个后继作为新状态，这些状态间相互通讯。如果一个状态找到多个好的后继，会告知其他状态一同继续搜索。

问题

基础版本的局部束搜索易于聚集到状态空间中的一个小局部区域，缺乏多样性，使得在寻找更优解方面与爬山法相似，容易陷入局部极值点。

缓解方案

一种变种是 随机束搜索（Stochastic Beam Search），类似于随机爬山法，能减轻陷入局部极值点的问题。随机束搜索不再选择 $k$ 个最好的后继，而是根 据一个函数计算出与后继优劣程度相关的值，并以此为概率选择 $k$ 个后继。

随机束搜索类似于 “自然选择法则”：适者生存概率高，不适者死亡概率高。

遗传算法（Genetic Algorithms）

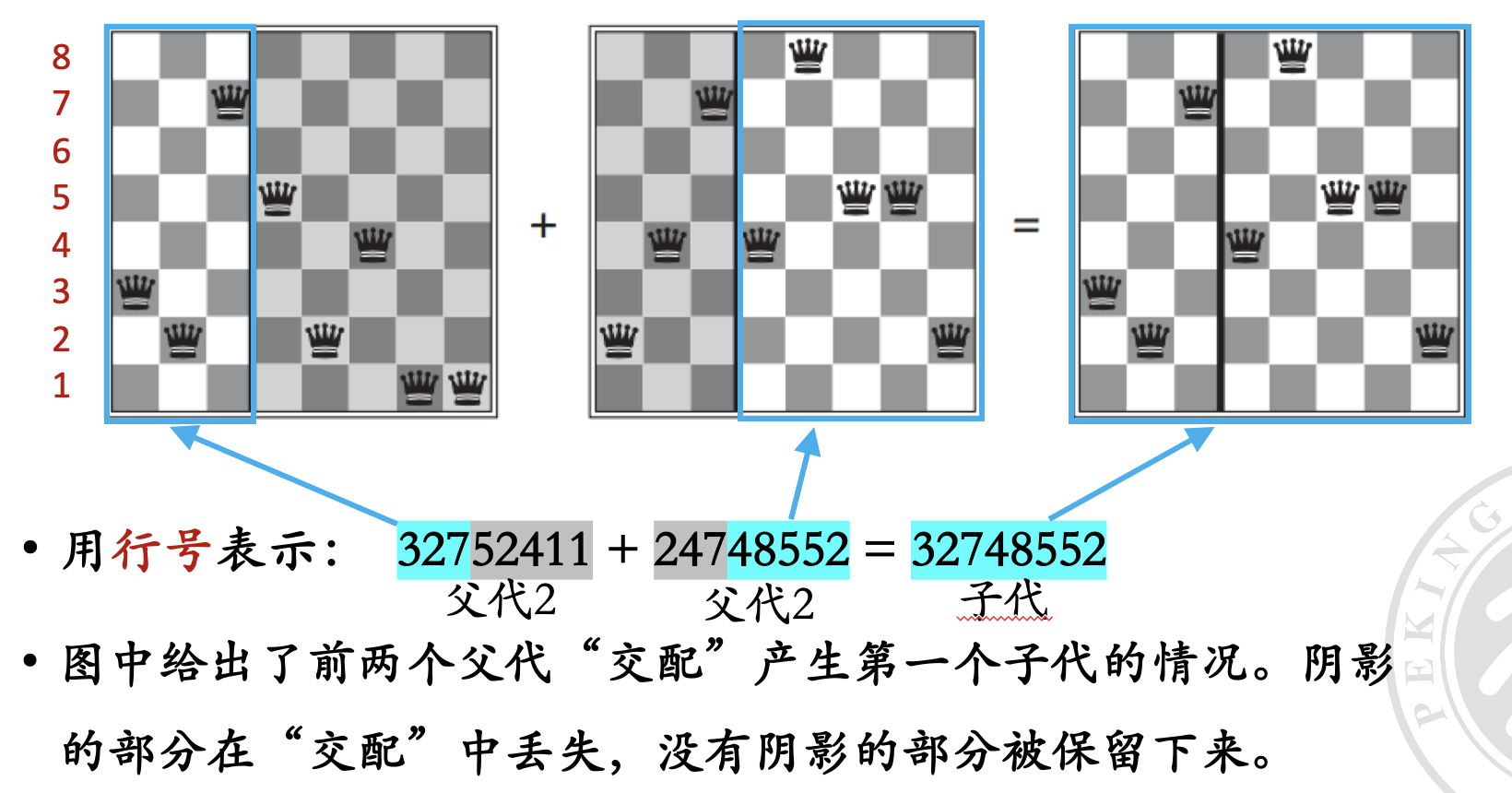
遗传算法是 随机束算法 的一个变种。与单个状态产生后继节点不同，遗传算法的后继节点是由 两个父状态结合 产生的。这类似于父母生成孩子的过程，因此称为遗传算法。

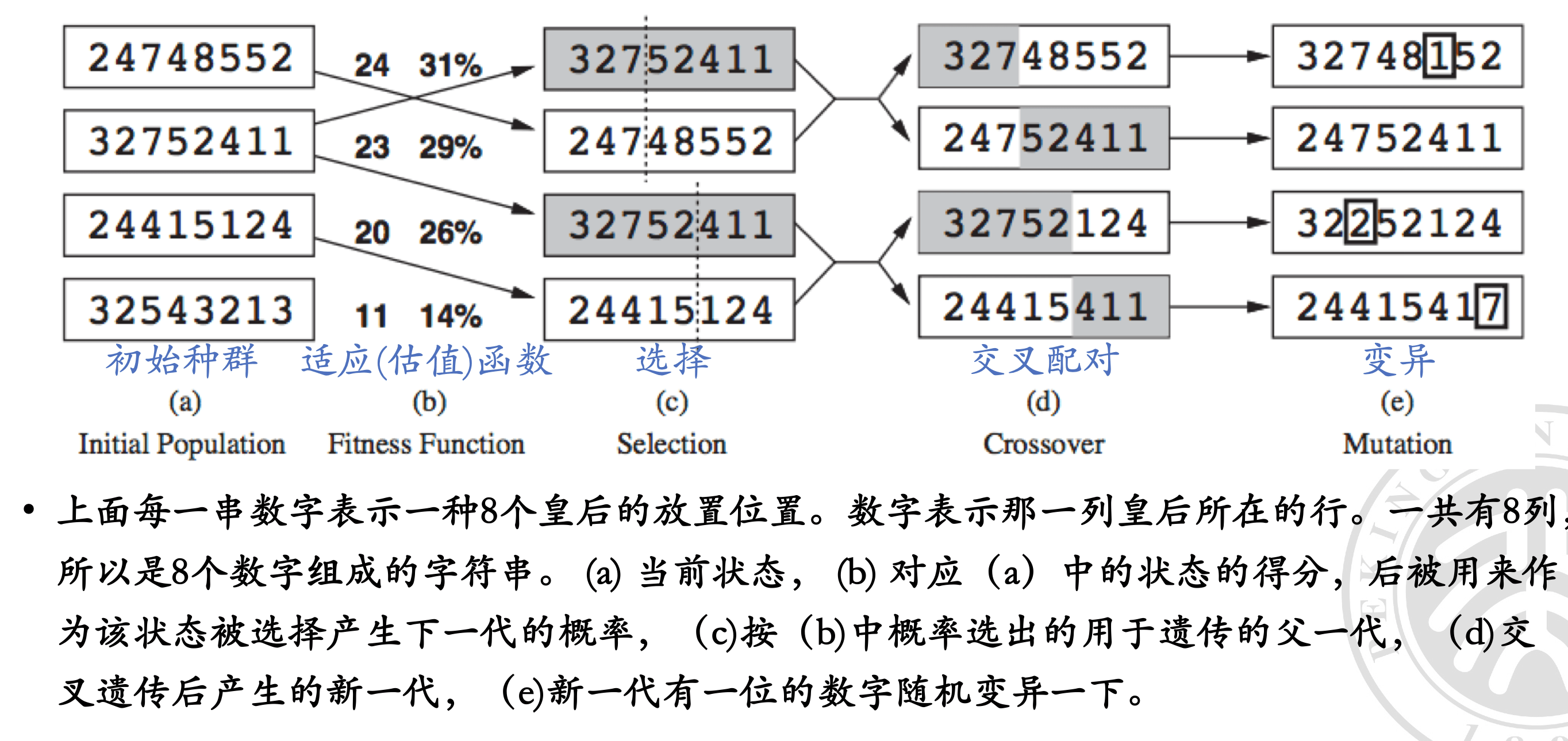
伪代码

主要特点

后代多样性大：遗传算法类似于 高级生物的有性繁殖，后代多样性大，变异概率高，不易陷入局部最优。

注意，这也同时导致了遗传算法的不稳定性。

遗传算法结合了 爬山法 和 随机探索，并在并行的搜索线程中交换信息。

交换子串 是遗传算法的主要优点，可以将优秀的功能块组合起来，提高后代的质量。
数学上，如果父代编码是随机的，交叉并不会带来好处。
直觉上，交叉可以将 具有良好功能的块 组合在一起，从而产生更好的下一代。

模式与状态

模式 Schema：在遗传算法中，模式（Schema）指的是一种部分子串，可以包含特定位置的固定值，也可以有任意值。例如，在一个二进制字符串中，模式 1*0 表示以 1 开头，以 0 结尾，中间的位可以是 0 或 1。
模式的优越性：如果一个模式在群体中表现得比平均水平好，那么这个模式会更有可能通过遗传操作（选择、交叉、变异）传递给下一代。这意味着，具有这种模式的个体数量会在后代中增加。
良好模式的积累：当一个模式能够很好地表达问题中的重要特征时，遗传算法的表现会更好。
状态的良好表达：为了使遗传算法表现良好，问题的状态需要被良好地表达。这意味着在编码方案中，重要特征和模式需要被明确地表示出来，以便遗传算法能够有效地选择和遗传这些特征。

连续空间中的局部搜索

例子：地图上新建机场

目标：在地图上新建三个机场，使每个城市与离它最近的机场的距离的平方和最小。

状态空间：每个机场的坐标 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ 。这是一个六维空间。

目标函数：

f(x_1,y_1,x_2,y_2,x_3,y_3)=\sum_{i=1}^3\sum_{c\in C_i}[(x_i-x_c)^2+(y_i-y_c)^2]

其中 $C_i$ 表示离机场 $i$ 最近的城市集合。目标是使 $f$ 最小。

离散化方法

通过将地图坐标离散化来解决连续问题。

每次移动一个机场的 $x$ 或 $y$ 坐标 $±δ$ ， $δ$ 越小，精度越高。
每个机场的当前状态有 12 个可能的邻居状态。

局部搜索算法

状态： $(x_1, y_1, x_2, y_2, x_3, y_3)$
评估函数： $f(x_1, y_1, x_2, y_2, x_3, y_3)$
邻居：一个机场的（ $x_i$ 或 $y_i$ $±\delta$ ）

建模

初始状态： $S_0 = (x_1, y_1, x_2, y_2, x_3, y_3)$ ，随机位置
动作：任何一个 $x_i$ 或 $y_i$ 都可以 $\pm\delta$ （12 个合法动作）
状态转移：采取动作后的位置（转移到 12 个邻居状态之一）
目标状态：使得 $f(x_1, y_1, x_2, y_2, x_3, y_3)$ 最小的 $x, y$ 取值
状态估值函数： $h = f(x_1, y_1, x_2, y_2, x_3, y_3)$

注意事项

可以使用前面介绍的任何局部搜索算法，例如爬山算法、模拟退火算法等。
离散化精度（ $δ$ ）会影响搜索结果的准确性。
需要考虑如何处理多个机场同时移动的情况。

优化方法

爬山 / 随机爬山 / 模拟退火
梯度下降 / 上升：
若函数可微，可以借助梯度信息来更新（而不需要求具体的离散后的邻居的估值）：
$x\leftarrow x\pm\nabla f(x)$
其中：
- $\alpha$ 是学习率 / 步长
  - 如果 $\alpha$ 太小，需要太多的步骤、更新慢
  - 如果 $\alpha$ 太大，搜索可能会越过极值点
- $\nabla f(x)$ 是梯度
- $\pm$ 对应不同的优化方向。
若估值函数不可微，则使用 经验梯度 的值法

和在离散空间一样，在连续空间里，局部搜索算法的最大难题仍是 局部极值和平台。为此，采用和离散空间一样的随机重启和模拟退火经常是有效的。

最小化冲突算法

最小化冲突算法用以解决 约束满足问题（CSP）。

约束满足问题（CSP, Constraint Satisfaction Problem）：在一组变量和一组约束条件下寻找一个变量赋值的过程，使得所有变量满足给定的约束条件。

CSP 的细节在后文讨论。

最小化冲突算法伪代码

\begin{array}{l} \text{// 定义函数 MIN-CONFLICTS，输入为约束满足问题 csp 和最大步数 max\_steps，返回一个解或失败} \\ \textbf{function} \ \text{MIN-CONFLICTS}(csp, max\_steps) \ \textbf{returns} \ \text{a solution or failure} \\ \quad \text{// 输入：csp，一个约束满足问题} \\ \quad \text{// max\_steps，放弃前允许的最大步骤数} \\ \quad \text{// current 是 csp 的一个初始完全赋值} \\ \quad \text{current} \leftarrow \text{an initial complete assignment for } csp \\ \quad \text{// 从 1 到 max\_steps 进行循环} \\ \quad \textbf{for} \ i = 1 \ \textbf{to} \ max\_steps \ \textbf{do} \\ \quad \quad \text{// 如果 current 是 csp 的一个解，则返回 current} \\ \quad \quad \textbf{if} \ current \ \textbf{is a solution for} \ csp \ \textbf{then return} \ current \\ \quad \quad \text{// var 是从 csp.VARIABLES 中随机选择的一个冲突变量} \\ \quad \quad \text{var} \leftarrow \ \text{a randomly chosen conflicted variable from } csp.\text{VARIABLES} \\ \quad \quad \text{// value 是使 CONFLICTS(var, v, current, csp) 最小的 var 的值 v} \\ \quad \quad \text{value} \leftarrow \ \text{the value } v \ \text{for } var \ \text{that minimizes CONFLICTS}(var, v, current, csp) \\ \quad \quad \text{// 在 current 中设置 var = value} \\ \quad \quad \text{set } var = value \ \text{in } current \\ \quad \text{// 如果循环结束仍未找到解，则返回失败} \\ \quad \textbf{return} \ \text{failure} \end{array}

八皇后问题的 CSP 建模

我们可以通过以下步骤将八皇后问题建模为一个 CSP：

变量定义：定义 8 个变量，每个变量表示一个皇后的位置。通常用 $Q_i$ 表示第 $i$ 行上的皇后所在的列位置。
变量取值范围：每个变量 $Q_i$ 的取值范围是 $\{1, 2, 3, 4, 5, 6, 7, 8\}$ ，表示皇后可以放在第 $i$ 行的任意一列。
约束条件
- 不同变量取值不同：即 $Q_i \neq Q_j$ （不同的皇后不能在同一列）。
- 不在同一对角线：即 $|Q_i - Q_j| \neq |i - j|$ （不同的皇后不能在同一对角线上）。

算法

初始化：随机放置 8 个皇后，使其符合所有行和列约束。
冲突检测：计算当前放置下的冲突数，即有多少对皇后彼此攻击。
冲突最小化：通过移动某个皇后减少冲突。例如，选择冲突最多的皇后，尝试移动到其他列，看哪个位置的冲突最少。
迭代：重复冲突检测和最小化，直到没有冲突（即找到解）或达到预定的最大迭代次数。

约束满足问题 CSP

约束满足问题将一个系统和它的状态当作一个整体，寻找状态解。

一个约束满足问题有三个组成部分， $X$ ， $D$ 和 $C$ ：
- $X$ 是变量， $\{X_1, X_2,..., X_n\}$ 。
- $D$ 是值域， $\{D_1,..., D_n\}$ ，每个变量一个值域（取值范围）。
- $C$ 是约束，用于描述变量取值之间的关系。
每个值域 $D_i$ 包含一组对于变量 $X_i$ 可行的取值 $\{V_{i_1},..., V_{i_m}\}$ ；每个约束条件 $C_j$ 包含一对数值 $\langle scope, rel\rangle$ ， $scope$ 是约束条件中涉及的变量， $rel$ 定义了变量的取值范围之间的关系。

CSP 问题的解

在 CSP 问题中，令每个变量一个取值， $\{X_1=v_1, X_2=v_2,...\}$ ，如果 不违背任何一个约束条件，则称为这个 CSP 问题的一个 可行解。可能存在多个可行解。
如果我们给定一个解的评价方式，则我们还可以寻找一个 最优解。最优解不一定是可行解，但是 是可以找到的最好的解。

在实际约束问题中，我们可能需要寻找：

一个可行解
全部可行解
一个最优解

把问题建模成约束满足问题 CSP 的原因

表示能力强：CSP 可以表示很宽泛的类别的问题。设计通用 CSP 求解器，使用 自动优化技术 迅速排除大量的无关搜索空间，比基于状态空间的搜索算法更快。
可解释性：CSP 的约束条件使得我们容易知道为什么某个赋值不是解（违背了哪个约束），并可以立即放弃对当下路径后续探索。

许多使用传统方法不能解出的问题，建模成 CSP 问题可以很快地解出。

CSP 模型变量的类型

变量 $X$ ：类型可以是 离散的，也可以是 连续的。

值域 $D$ ：可以是 有限的，也可以是 无限的。

离散类型变量的取值 也可以是 无限的，例如整数，或者是 字符串。

CSP 约束条件的类型

用 C 描述约束的量来对其分类

一元约束 （unary constraint）：针对单个变量取值的约束。
二元约束 （binary constraint）：涉及到两个变量。
三元约束 （ternary constraint）：例如，变量 $Y$ 的取值要在变量 $X$ 和 $Z$ 之间，表示成三元约束，Between $(X,Y,Z)$ 。
全局约束 （global constraint）：含有任意多个变量，最常见的全局约束是 All diff，其含义是所有变量的取值必须互不相同。

用 C 是否是强制性的来分类

绝对约束：违背这种约束意味着排除了成为解的可能性。
优先约束 （preference constraints）：用来描述哪些是优先选择的，可用表示求最优解。这意味着，满足这个约束越好，获得的解就越好。
优先约束一般会实现为给每个变量的取值增加一个代价（costs），这样，含有优先约束的 CSP 问题就称为约束优化问题（constraint optimization problem），简称 COP。

约束传播：CSP 中的推理

在普通的状态空间搜索中，我们能做的事情 只有搜索。

而在 CSP（约束满足问题）中，除了搜索，还可以进行 推理（也称为约束传播）。

约束传播：通过使用约束来 减少一个变量的可能取值，从而减少其他变量的可能取值。约束传播可以与搜索相结合，也可以先进行约束传播的预处理，然后再进行搜索。

有时，预处理就可以解决全部问题，不用再进行搜索。

点一致

点一致指变量的所有取值都满足一元约束。通过点一致性算法去除不满足一元约束的取值。

例：如果 $X$ 的取值范围是 $\{1, 2, 3\}$ ，且有约束 $X \neq 2$ ，那么经过点一致处理后， $X$ 的取值范围变为 $\{1, 3\}$ 。

边一致

边一致指变量的所有取值都满足二元约束。

例：如果 $X$ 和 $Y$ 的取值范围分别是 $\{1, 2\}$ 和 $\{2, 3\}$ ，且有约束 $X < Y$ ，那么经过边一致处理后， $X$ 的取值范围变为 $\{1\}$ ， $Y$ 的取值范围变为 $\{2, 3\}$ 。

我们称一个 网络是边一致 的，如果每个变量相对于 其他任意变量 都是边一致的。

约束传播的应用

使用约束传播可以去除不合理的解，从而缩小值域，提高解决问题的效率。

约束满足问题的通用求解方法

通用约束求解器：如 MiniZink
自动生成求解程序：如 PDL2C