VLA Frontier

AIGC Declaration#

本文使用了 AIGC 来提高效率，其中可能存在谬误，我已尽力检查并校对，但仍不保证完全准确，欢迎指正。

本文依赖于我编写的 arXiv Tex 源码获取 Pipeline，这里是 Repo ↗，欢迎使用！

HybridVLA#

Paper ↗

Insight#

1. 传统自回归（AR，RT-2/OpenVLA）方法为了将动作作为 token 用 LLM 去预测，将动作离散化，破坏了动作连续性
2. 扩散方法（Diffusion，CogACT/DiVLA）的扩散头独立于 LLM，无法利用语言模型的推理能力
3. 设计一种办法协同 AR 和 Diffusion，从而兼顾两者的优点，同时充分利用 LLM

Method#

Arch#

Backbone：

1. Vison Encoder：DINOv2（语义特征）+ SigLIP（细粒度特征）
2. Prompt Encoder：LLAMA-2 (7B) / Phi-2 (2.7B)

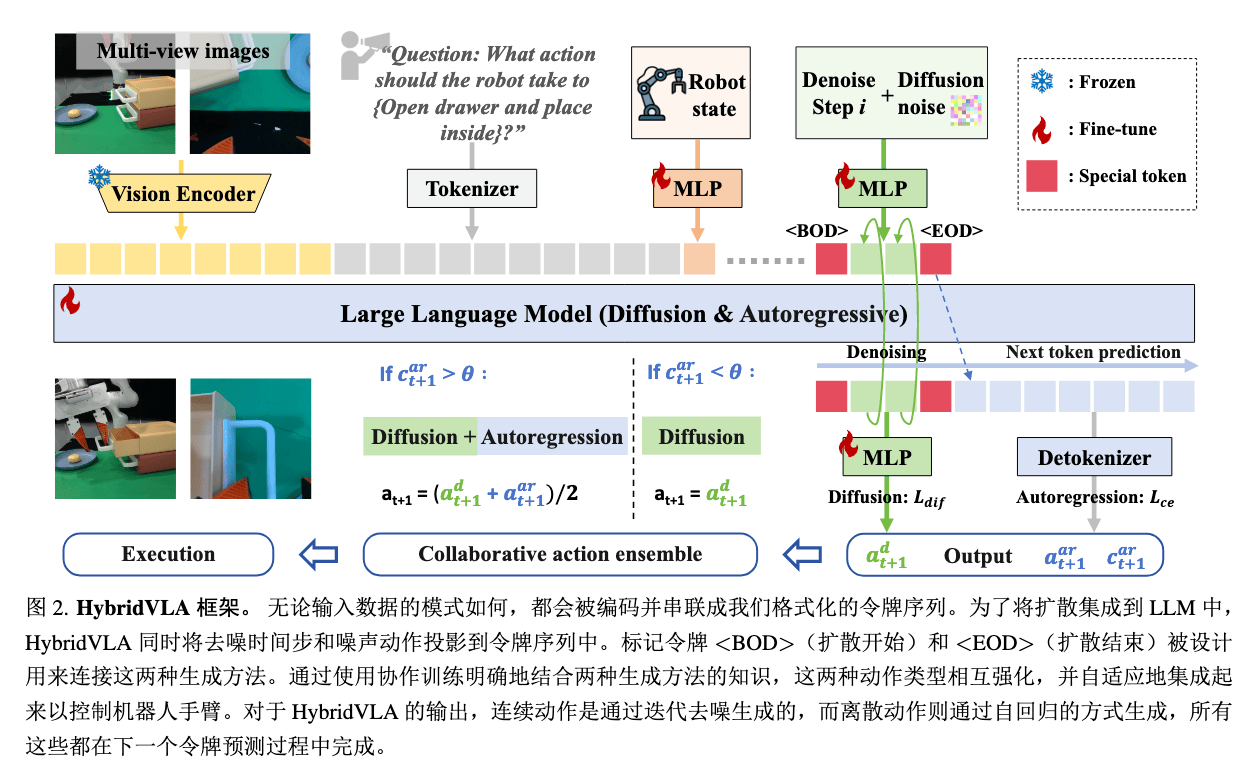
整体 Token 序列结构：

$$\text{Input Tokens} = \underbrace{[V_1,...,V_N]}_{\text{视觉}} \oplus \underbrace{[L_1,...,L_M]}_{\text{语言}} \oplus \underbrace{[R]}_{\text{机器人状态}} \oplus \underbrace{[\text{<BOD>}, a^{i}_t, i, \text{<EOD>}]}_{\text{扩散部分}} \oplus \underbrace{[A^{ar}_1,...,A^{ar}_K]}_{\text{AR 动作}}$$

1. 编码后（V,L,R），插入一个特殊的扩散开始 Token $\text{<BOD>}$ 与掩码 $\text{<MASK>}$

   $$\text{Input Tokens} = \underbrace{[V_1,...,V_N]}_{\text{视觉}} \oplus \underbrace{[L_1,...,L_M]}_{\text{语言}} \oplus \underbrace{[R]}_{\text{机器人状态}} \oplus \text{<BOD>} \oplus \text{<MASK>}$$

2. 然后进行扩散 Token 预测，使用得到的 Token 进行去噪，得到扩散动作 $a^d$

   $$a^d = a^0 = [\Delta x, \Delta y, \Delta z, \text{Roll}, \text{Pitch}, \text{Yaw}, \text{Gripper(0/1)}]$$

3. 对得到的扩散动作 $a^d$，重新使用 MLP 映射回 LLM，得到 $e_{a^d}$，插入特殊的扩散结束 Token $\text{<EOD>}$，重构得到序列

   $$[V][L][R][\text{<BOD>}][e_{a^d}][\text{<EOD>}][\text{<MASK>}]$$

4. 基于新序列预测 AR Token，再经过 Detokenizer，得到动作 $a^{ar}$（动作离散到 256 个动作区间，概率值）

5. 计算 AR 动作置信度 $c^{ar}$

   $$c^{ar} = \frac{1}{7}\sum_{k=1}^7 \max(p(A_k))$$

6. 根据置信度，判断是要融合 AR 动作与扩散动作还是直接使用扩散动作

   $$a_{final} = \begin{cases} 0.5a^d + 0.5a^{ar}, & \text{if } c^{ar} > 0.96 \\ a^d, & \text{otherwise} \end{cases}$$

直观理解：

1. 扩散模式：自动驾驶（精确控制油门 / 刹车）
2. AR 模式：语音导航（“前方路口左转”）
3. 当导航指令清晰时（高置信度），自动驾驶会参考语音提示；当导航模糊时，完全依赖自动驾驶

现在，HybridVLA 既保持了语言模型的强推理能力，又获得了物理级的动作连续性，突破了传统 VLA 模型的性能瓶颈。

Loss function#

$$\mathcal{L}_{dif}=E_{a,i,c}||\epsilon-\epsilon_\pi(a_t^i,i,c)||^2 \\ \mathcal{L}_{hybrid}=\mathcal{L}_{dif}+\mathcal{L}_{ce}$$

Trick#

• KV 缓存加速
• 降低 Diffusion 去噪步数以加速生成

Question#

为什么 AR 不加 diffusion，难道没语义了吗

ManipLLM#

Paper ↗

Why#

• 基于有限数据集学习的方法见过的物品类别是有限的，难以泛化到现实世界
• 过往的模型无法解释自身的结果（可解释性差），是个黑箱

Insight#

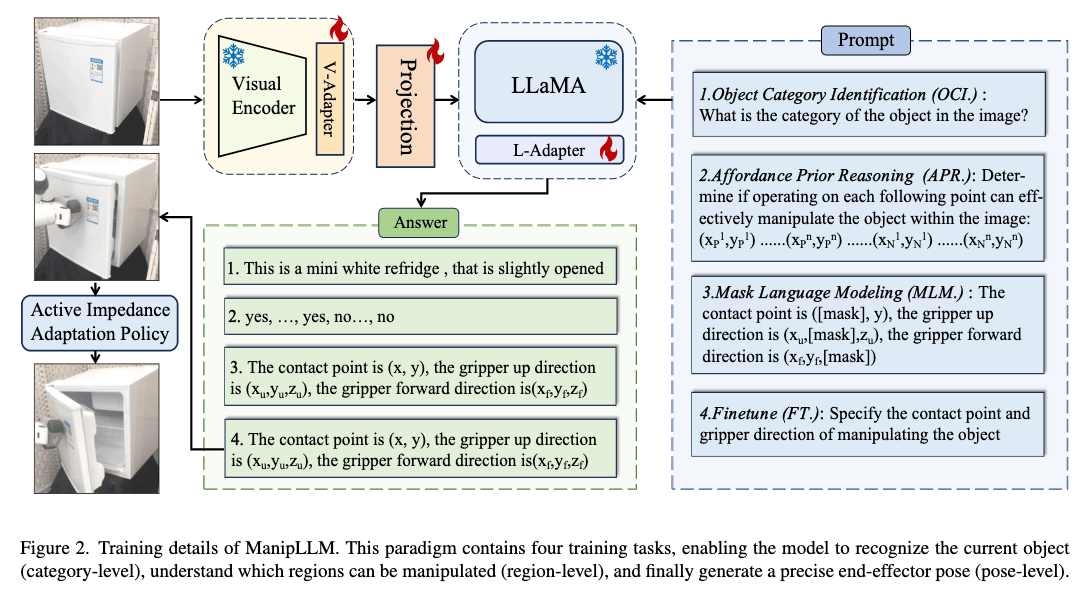
1. 通过 类别 → 区域 → 位姿 的渐进式训练将 MLLM（多模态大语言模型，Multimodal Large Languege Model）基于互联网级别数据所习得的常识和推理能力与之前看似黑箱的机器人操作去逐渐对齐，类似 COT 思维链完成渐进式思考，从而得到由粗到细的高可解释性动作预测
2. 直接让 MLLM 去对图片进行预测哪里可以动可能效果是不 OK 的，但根据 Affordance Map 生成若干个点来让 MLLM 进行选择（选择题比填空题好做）是 OK 的。

Method#

Arch#

Backbone：

• 视觉编码器：CLIP 的 ViT
• 文本编码器：LLaMa 的 Tokenizer
• 多模态对齐：通过适配器（Adapter）将视觉特征与 LLaMa 的文本空间对齐，仅微调适配器参数，保留 MLLM 原有知识。

Loss Function#

$\mathcal{L}_A$ 可供性损失#

目标：教会模型识别物体表面可操作区域

训练方式：

1. 首先根据可供性图 $\mathcal{A}$ 来在图片中随机选择一系列点，包括 $n$ 个正样本（$\mathcal{A} \geq 0.8$）、 $n$ 个负样本（$\mathcal{A} \geq 0.8$），分别标记为 1、0
2. 将点的位置送入 MLLM，进行提问：“确定在以下每个点上操作是否可以有效地操纵图像中的对象？” + $\{x_i, y_i\}^{2n}_{i=1}$
3. 获得模型输出词元概率序列 $\{p_i\}^n_{i=1}$，注意这里不是 0/1，而是 LLM 输出此处为 True 这个词元的概率
4. 计算交叉熵损失： $$\mathcal{L}_A = -\frac{1}{2n} \sum_{i=1}^{2n} \left[ y_i \log p_i + (1 - y_i) \log (1 - p_i) \right]$$

$\mathcal{L}_M$ 语言建模损失#

目标：通过 “填空” 训练模型预测被遮挡的位姿参数

训练方式 MLM（Mask Language Modeling，完形填空） ：

1. 随机遮挡坐标或方向分量，如将 “接触点是 $(80,120)$” 改为 “接触点是 $(\text{[MASK]},120)$”
2. 每个被遮挡值离散化为 100 个区间
3. 模型预测被遮挡位置的类别概率分布 $q_j$，计算交叉熵（真实标签以 one-hot 编码，$c_j$ 为真实类别编号）： $$\mathcal{L}_M = -\sum_{j \in \text{masked}} \log q_j[c_j]$$

$\mathcal{L}_F$ 位姿预测损失#

目标：直接训练模型预测完整位姿参数，包括：

• 接触点坐标 $(x, y)$
• 夹爪上方向 $(x_u, y_u, z_u)$
• 夹爪前方向 $(x_f, y_f, z_f)$

注：三维空间坐标由深度图投影得到。

训练方式：类似 $\mathcal{L}_M$，用 MLM 方式来计算损失

总损失#

$$\mathcal{L} = \mathcal{L}_A + \mathcal{L}_M + \mathcal{L}_F$$

注意这里，$\mathcal{L}_A$ 提供的区域先验可以帮助 $\mathcal{L}_M$ 和 $\mathcal{L}_F$ 更准确定位接触点。

1. $\mathcal{L}_A$ 先教会模型 “哪里能操作”
2. $\mathcal{L}_M$ 再训练 “如何补全参数”
3. $\mathcal{L}_F$ 最终实现 “端到端预测”

主动阻抗适应策略#

问题：方向预测可能存在误差

解决办法：在初始方向附近随机添加多个扰动方向，随后挨个试，每个施加一个固定的阻抗力，测量位移，选择最大的位移方向。

测试时适应（TTA）#

问题：Sim-to-Real 差异（如光照、纹理变化）导致位姿预测偏移。

策略：在线更新视觉适配器（Visual-Adapter，连接 CLIP 视觉编码器和 LLaMa 语言模型，参数很少，就是一个轻量 MLP）参数

1. 输入当前测试样本的位姿预测结果 $(x,y)$
2. 根据实际操作成败生成二元标签（成功 → “yes”，失败 → “no”）
3. 通过 $\mathcal{L}_A$ 微调视觉适配器，适应真实场景的视觉特征。

π0#

Why#

1. 现有数据集太少，无法习得通用能力
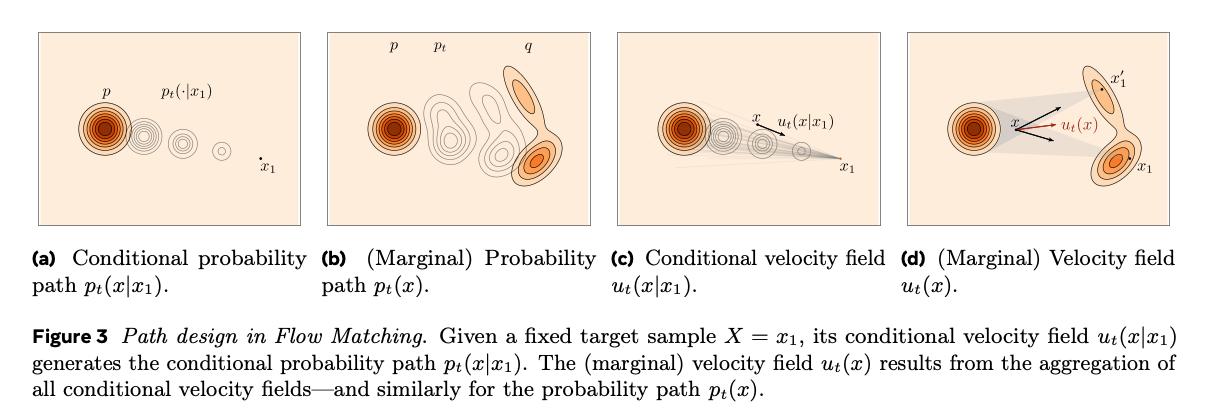
2. 基于 AR 的动作生成方法难以实现高频控制（但现有的基于扩散的模型已经改进了一些），流匹配是扩散的一种变体，适合生成高频、复杂、精细的动作块

Insight#

1. VLM + Flow Matching = new VLA
2. 不能只在高质量数据集上训练，否则鲁棒性（容错性）不强，无法在真实世界中使用，解决方案是先在低质量、大量的混合机器人数据上学习，然后再在高质量数据集上进行微调，精进技能

Method#

基本就是引入了流匹配来替换扩散模型，这是一种相较于扩散更直观的生成模型，关于流匹配的推导、代码和直观讲解可以参见 Meta 的综述 ↗。

RoboFlamingo#

Paper ↗ / 作者解读 ↗

Insight#

感觉没啥新的，可能是我看的顺序问题，先看了今年 / 去年的，潜移默化地感觉这个结构似乎已经是一个范式了。

Method#

Arch#

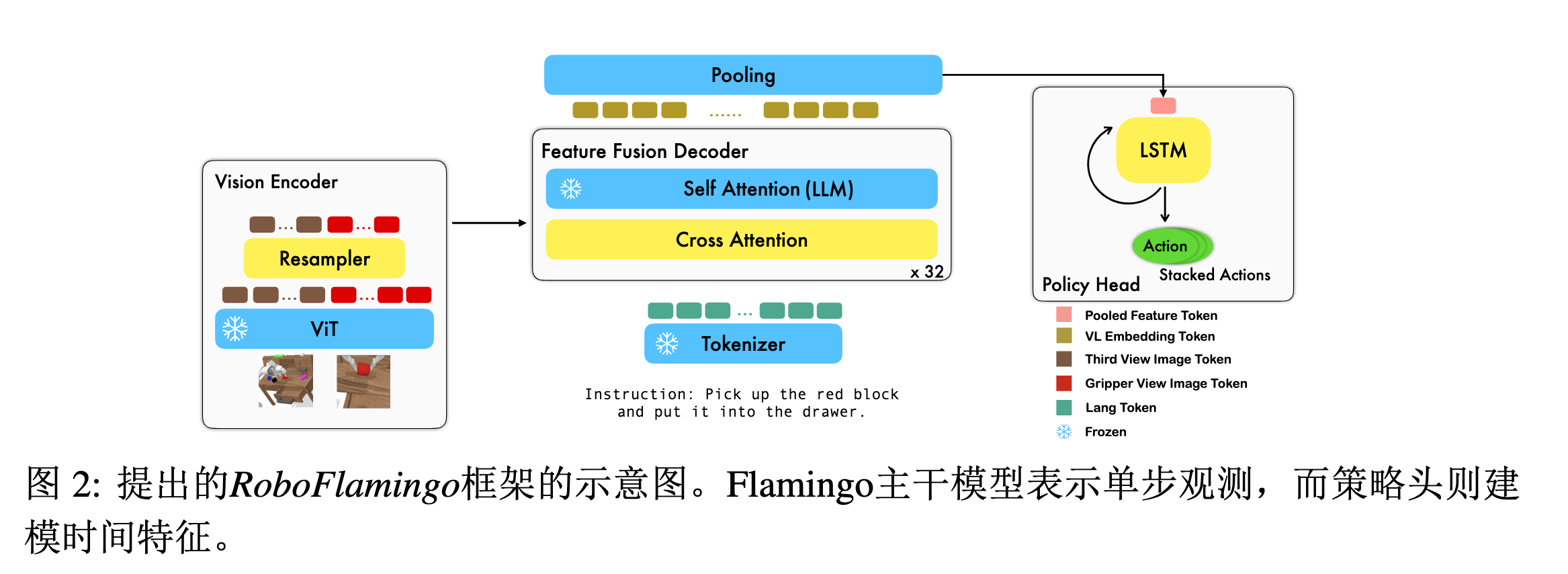
1. ViT（预训练） + Resampler 下采样（通过自注意力机制实现）降低 Token 数量，得到视觉 Token

   $$\hat{X}_t^v=\text{ViT}(I_t,G_t) \\ \text{Resampler: }K_R=\hat{X}_t^vW_K^R, V_R=\hat{X}_t^vW_V^R, X_t^v=\text{softmax}(\frac{Q_RK_R^T}{\sqrt{d}})V_R$$

2. LLM（预训练）得到文本 Token

   $$X = X_t^1=\text{LLM}(L_t)$$

3. 特征融合：堆叠 $L$ 层解码器，每层结构包括：

   1. 使用交叉注意力，以 Text Token 做 Query，Visual Token 做 Key / Value，进行残差连接
   2. 随后进行自注意力，依旧进行残差连接，从而完成视觉与语言特征的融合
   $$\begin{aligned} &\hat{X}_t^l=\text{Tanh}(\alpha)\cdot\text{MLP}(A(X_t^lW_Q^C,X_t^vW_K^C,X_t^vW_V^C))+X_t^l,\\ &X_t^{l+1}=\text{MLP}(A(\hat{X}_t^lW_Q^S,\hat{X}_t^lW_K^S,\hat{X}_t^lW_V^S))+\hat{X}_t^l \end{aligned}$$

4. max pooling 后送入策略头，以一个循环模型（LSTM）进行时序建模，直接预测 7 DoF 动作

   $$\tilde{X}_t=\mathrm{MaxPooling}(X_t)\\ h_t=\mathrm{LSTM}(\tilde{X}_t,h_{t\boldsymbol{-}1})\\ a_t^{pose},a_t^{gripper}=\mathrm{MLP}(h_t)$$

Train#

监督信号：专家示范动作

• 位姿预测：MSE 损失
• 夹爪状态：BCE 损失
• 总损失： $$\mathcal{L} = \sum_t \|a_t^{pose} - \hat{a}_t^{pose}\|^2 + \lambda \cdot \text{BCE}(a_t^{grip}, \hat{a}_t^{grip})$$

微调策略：

• 仅训练：重采样器参数 + 交叉注意力层 + 策略头
• 冻结：ViT 参数 + 语言模型参数
• 结果：参数量 <1% 的微调，高效且防过拟合

RoboMamba#

Paper ↗

Mamba#

Mamba Youtube 讲解 ↗ / CSDN ↗

传统模型的问题：

1. Transformer 自注意力机制的计算复杂度为 $O(L^2)$（$L$ 为序列长度），资源需求量大

2. RNN 等在反向传播的时候需要沿着时间维度逐步进行（Backpropagation through time），无法并行训练；且长程依赖关系容易造成梯度消失 / 爆炸，尽管 LSTM 等通过门控机制缓解，但并未完美解决。

   RNN 的本质是一个这样的函数：

   $$h_{t+1} = f(h_t, x_{t+1})$$

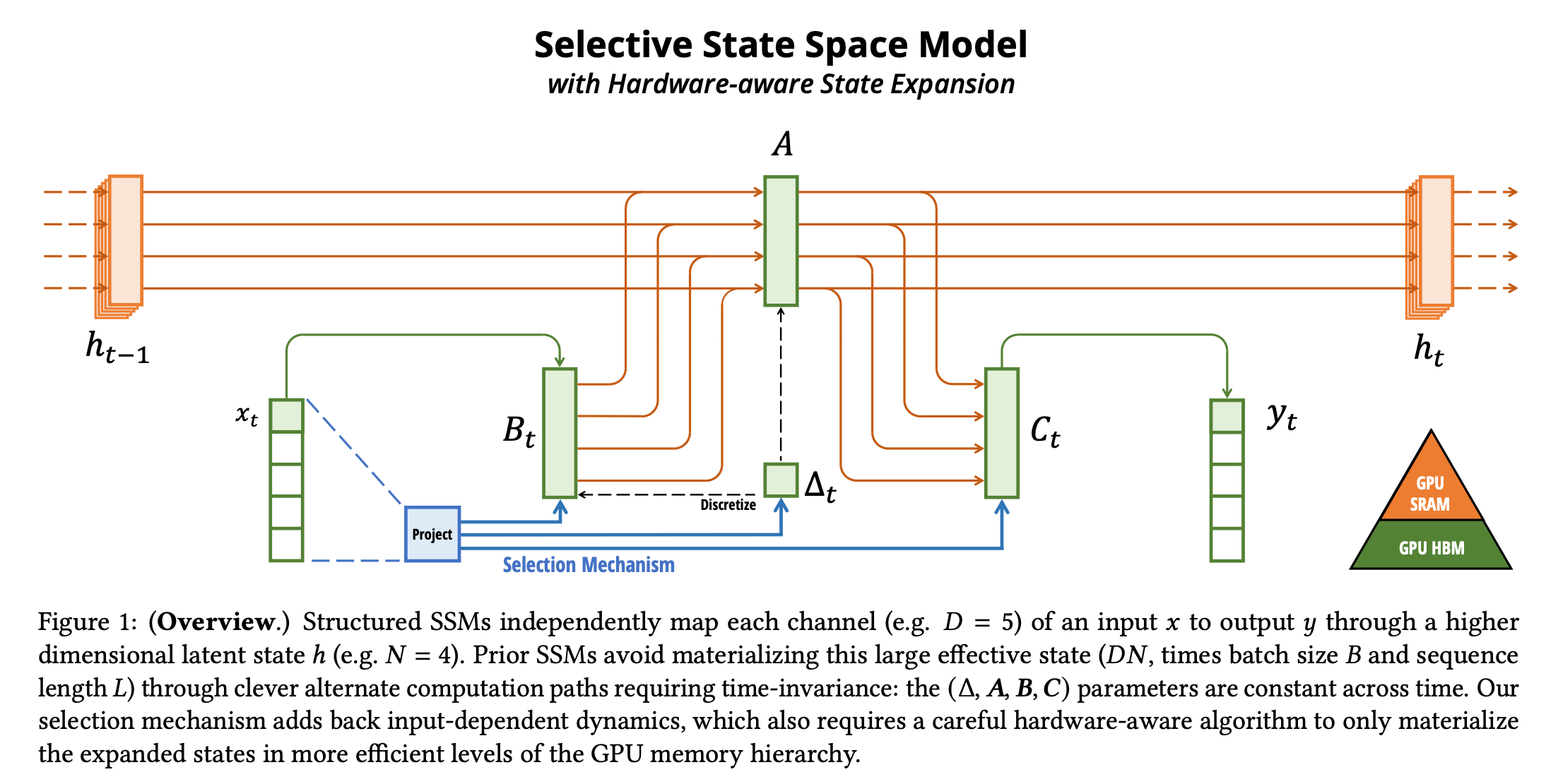
SSM#

1. 本质类似 RNN，但是在训练的时候无需像 LSTM 一样总要等到隐状态沿着时间维度完整前传，而是类似 Transformer，可以并行地处理所有 Token
   1. 隐状态之间没有非线性，而是具有了很好的线性性质，可以直接化为一个完整的矩阵乘法
   2. 没有时间依赖性（线性非时变系统），$A$ 和 $B$ 在整个前向推理过程中不变，从状态 1 转到状态 2，和从状态 2 转到状态 3 是一样的，换句话说聚合信息的方式是恒定的
2. 推理时像无隐状态的线性 RNN，可以并行地推导所有步骤的输出，而无需像 Transformer 一样以自回归地形式一个 Token 一个 Token 地输出（因为 Transformer 在推理过程中的注意力矩阵是动态构建的）

以下为 S4 的数学推导，摘录整理自 这里 ↗，补全了最后一步的跳步。

状态空间模型将系统的状态、输入和输出关系表示为：

$$\begin{aligned} \dot{x}(t) &= A(t)x(t) + B(t)u(t)\\ y(t) &= C(t)x(t) + D(t)u(t) \end{aligned}$$

其中，$A,B,C,D$ 是系数矩阵，$x(t)$ 是状态向量，$u(t)$ 是输入向量，$y(t)$ 是输出向量。

假定系数矩阵不随时间变化，这可以简化为线性非时变系统：

$$\begin{aligned} \dot{x}(t) &= Ax(t) + Bu(t)\\ y(t) &= Cx(t) + Du(t) \end{aligned} \tag{1}$$

容易发现，核心其实是第一个式子，但若直接对状态方程积分：

$$x(t) = x(0) + \int_0^t (Ax(\tau) + Bu(\tau))\mathrm{d}\tau$$

积分项包含 $x(\tau)$ 本身，但我们无法获取连续时间内所有 $x(\tau)$ 值，导致积分无法完成。

所以，我们将上式转换为离散形式：

$$x(k+1) = x(k) + \sum_{i=0}^k (Ax(i) + Bu(i))\Delta t$$

但这仍需要改造原方程，消除 $\dot{x}(t)$ 表达式中的 $x(t)$ 从而可以积分。

构造辅助函数 $\alpha(t)x(t)$ 并求导：

$$\frac{\mathrm{d}}{\mathrm{d}t}[\alpha(t)x(t)] = \alpha(t)\dot{x}(t) + x(t)\frac{\mathrm{d}\alpha(t)}{\mathrm{d}t}$$

代入状态方程 $(1)$：

$$\frac{\mathrm{d}}{\mathrm{d}t}[\alpha(t)x(t)] = \alpha(t)(Ax(t) + Bu(t)) + x(t)\frac{\mathrm{d}\alpha(t)}{\mathrm{d}t}$$

合并 $x(t)$ 的相关系数：

$$\frac{\mathrm{d}}{\mathrm{d}t}[\alpha(t)x(t)] = \left(A\alpha(t) + \frac{\mathrm{d}\alpha(t)}{\mathrm{d}t}\right)x(t) + B\alpha(t)u(t) \tag{2}$$

为消除导数中的 $x(t)$，令其系数为 $0$：

$$A\alpha(t) + \frac{\mathrm{d}\alpha(t)}{\mathrm{d}t} = 0$$

解得：

$$\alpha(t) = e^{-At}$$

代入 $(2)$：

$$\frac{\mathrm{d}}{\mathrm{d}t}[e^{-At}x(t)] = Be^{-At}u(t)$$

对此式积分：

$$e^{-At}x(t) = x(0) + \int_0^t e^{-A\tau}Bu(\tau)\mathrm{d}\tau$$

整理得到：

$$x(t) = e^{At}x(0) + \int_0^t e^{A(t-\tau)}Bu(\tau)\mathrm{d}\tau$$

在离散系统中：

• 定义采样时刻 $t_k$ 和 $t_{k+1}$，采样间隔 $T = t_{k+1} - t_k$
• 将连续时间积分区间分成离散子区间：

$$x(t_{k+1}) = e^{A(t_{k+1}-t_k)}x(t_k) + \int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)}Bu(\tau)\mathrm{d}\tau \tag{3}$$

采用零阶保持法，假设 $u(t)$ 在采样间隔内保持恒定：

$$\int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)}Bu(\tau)\mathrm{d}\tau = \int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)}\mathrm{d}\tau \cdot Bu(t_k)$$

代入 $(3)$，并使用 $T = t_{k+1} - t_k$：

$$x(t_{k+1}) = e^{AT}x(t_k) + \int_{t_k}^{t_{k+1}} e^{A(t_{k+1}-\tau)}\mathrm{d}\tau \cdot Bu(t_k)$$

引入变量替换 $\lambda = t_{k+1} - \tau$：

$$x(t_{k+1}) = e^{AT}x(t_k) + Bu(t_k)\int_0^T e^{A\tau}\mathrm{d}\tau$$

原文这里略有跳步，只需要展开矩阵指数然后假设 $A$ 可逆从而合并系数再重新合并成矩阵指数即可：

$$e^{A\tau} = I + A\tau + \frac{(A\tau)^2}{2!} + \frac{(A\tau)^3}{3!} + \dots$$ $$\begin{aligned} \int_0^T e^{A\tau} \mathrm{d}\tau &= \int_0^T \left( I + A\tau + \frac{(A\tau)^2}{2!} + \frac{(A\tau)^3}{3!} + \dots \right) \mathrm{d}\tau \\ &= \int_0^T I \mathrm{d}\tau + \int_0^T A\tau \mathrm{d}\tau + \int_0^T \frac{(A\tau)^2}{2!} \mathrm{d}\tau + \dots \\ &= T \cdot I + \frac{A T^2}{2} + \frac{A^2 T^3}{3 \cdot 2!} + \frac{A^3 T^4}{4 \cdot 3!} + \dots \\ &= \sum_{k=0}^{\infty} \frac{A^k T^{k+1}}{(k+1)!} \\ &= \sum_{m=1}^{\infty} \frac{A^{m-1} T^m}{m!} \quad \text{换元：} m = k+1 \\ &= A^{-1} \sum_{m=1}^{\infty} \frac{(A T)^m}{m!} \\ &= A^{-1} (e^{A T} - I) \end{aligned}$$

最终离散时间状态方程：

$$x(t_{k+1}) = e^{AT}x(t_k) + (e^{AT} - I)A^{-1}Bu(t_k)$$

容易想到这里还是会存在类似 RNN 的长程依赖问题，Mamba 最终其实相对于 S4 做了很多改进，包括 HiPPO（处理远程依赖性）等，这里就没详细去看了（逃）

Insight#

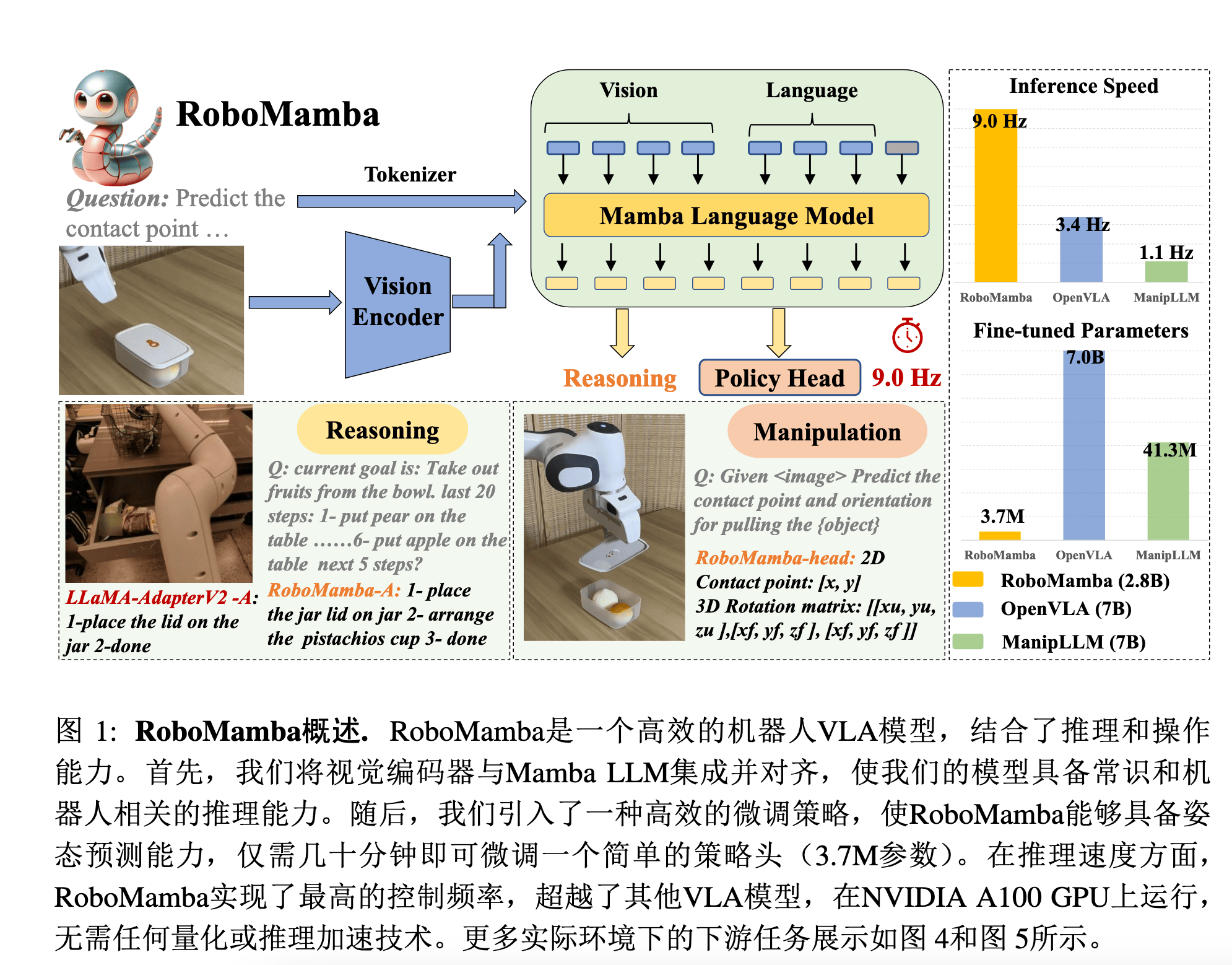
Training#

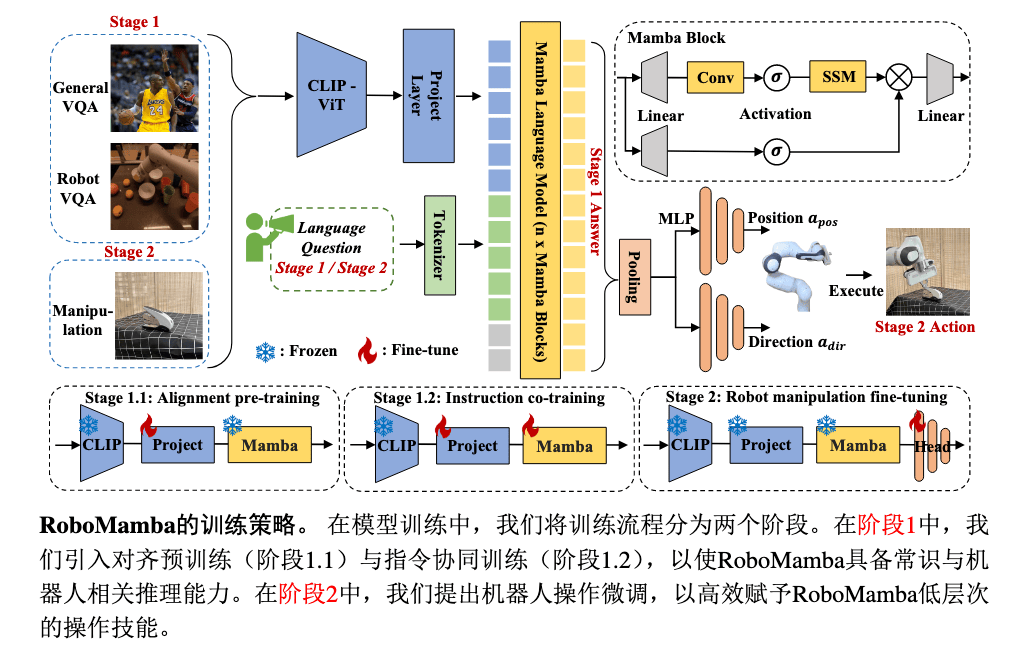
对齐预训练#

数据：LLaVA 图像 - 文本对

目的：使用单一 MLP 对齐视觉特征编码与 Mamba 词嵌入

冻结 CLIP、Mamba，仅微调 Project MLP 投影层。

令对齐预训练数据集为 $\mathcal{D}_a = \{(I_k, T_k)\}_{k=1}^N$，其中：

• $I_k \in \mathbb{R}^{W \times H \times 3}$：图像输入
• $T_k = [t_1^{(k)}, t_2^{(k)}, ..., t_L^{(k)}]$：对应的文本描述（token 序列）

那么：

$$p(y|I) = \text{Softmax}(\text{Mamba}([\text{Proj}(\text{Emb}(I)); \text{<question>}])) \\ \mathcal{L}_a = -\sum_{k=1}^N \sum_{t=1}^{L_k} \log p(t_t^{(k)} | t_{<t}^{(k)}, I_k)$$

指令协同训练#

目的：学习长程规划、物理常识等技能

数据：$\mathcal{D}_c = \mathcal{D}_{gen} \cup \mathcal{D}_{robot}$ 为混合指令数据集

• $\mathcal{D}_{gen}$：通用视觉指令数据（如 ShareGPT4V）
• $\mathcal{D}_{robot}$：高级机器人指令数据（如 RoboVQA）

冻结 CLIP，微调 Project MLP 投影层、Mamba。

先在通用的上面训练，然后再在高级数据集上训练，损失函数为交叉熵。

这里不知道有没有采用渐进式混合 $\mathcal{L}_c = \lambda \mathcal{L}_{gen} + (1-\lambda)\mathcal{L}_{robot}$

这个阶段挺重要的，原文说跳过此处训练直接进行动作微调时，成功率从 82.3% 骤降至 47.1%。

动作微调#

目的：训练动作策略头，获得操作能力

冻结 CLIP、Project MLP 投影层、Mamba，仅调整策略头。

$$\begin{align} \mathcal{L}_{pos} &= \frac 1N {\sum_{i=1}^N |a_\mathrm{pos} - a^{gt}_\mathrm{pos}|} \\ \mathcal{L}_{dir} &= \frac 1N {\sum_{i=1}^N \arccos\left (\frac{{\text{Trace}\Big(a^{gt}_\mathrm{dir}}^\top a_\mathrm{dir}\Big)-1}{2}\right )} \end{align}$$

注：两个旋转矩阵的乘积 $R^\top R_{gt}$ 表示相对旋转；对于旋转矩阵 $R$，其迹与旋转角度 $\theta$ 满足：

$$\text{Trace}(R) = 1 + 2\cos\theta$$

从而通过迹可直接计算两个旋转矩阵之间的角度差异。

GR-1#

Paper ↗ / Project Page ↗

Generative Robot-1

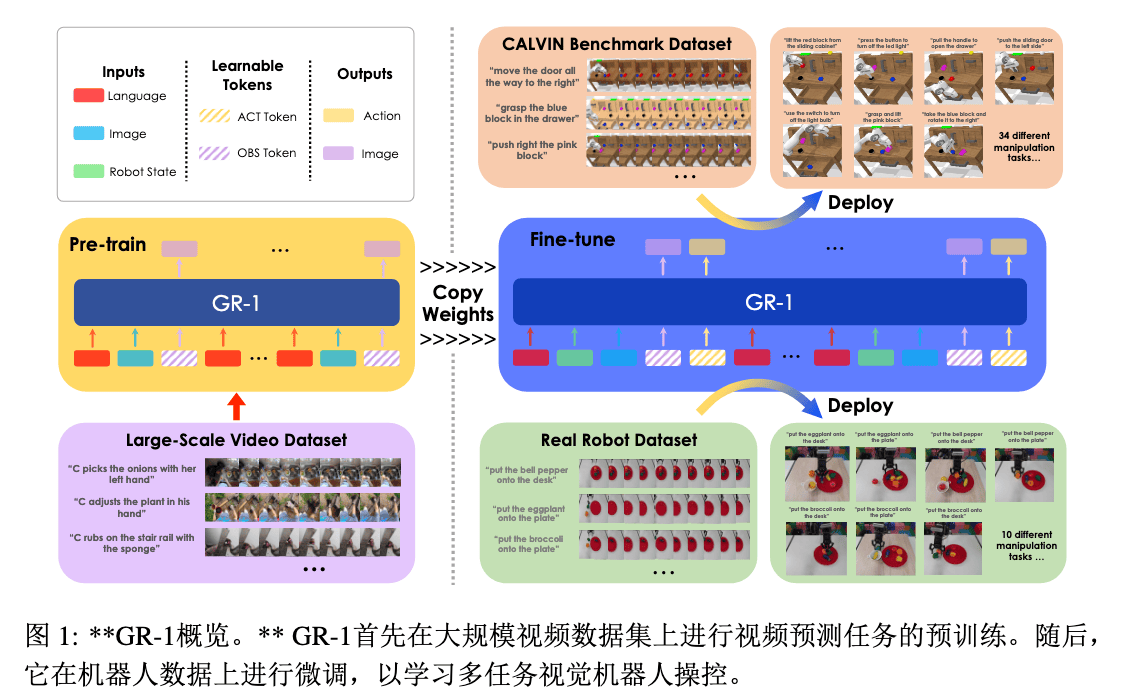
Insight#

1. 数据瓶颈突破：传统视觉机器人操作受限于小规模机器人数据（高采集成本），而视频数据与机器人轨迹具有内在一致性（时间序列 + 多模态）
2. 统一建模优势：GPT-style Transformer 可同时处理语言、图像、机器人状态，避免传统方法中多模块拼接的复杂性
3. 预训练 - 微调协同：视频预测任务（预测未来帧）隐式学习物理规律，迁移到机器人动作推理时提升泛化能力

核心贡献：首次证明大规模视频生成预训练可迁移到机器人操作，统一 GPT 架构实现多模态 - 多任务端到端学习。

Method#

Arch#

Backbone：

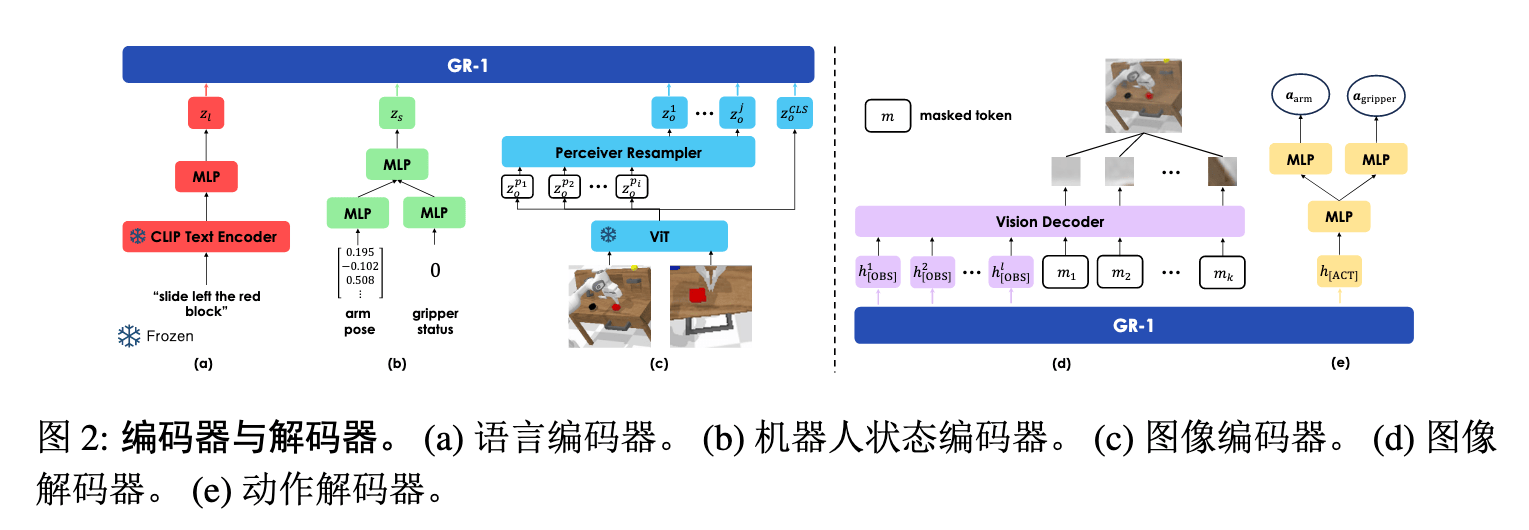
1. Vision Encoder：MAE 预训练的 ViT（图像 → patch tokens + CLS token）
2. Language Encoder：冻结的 CLIP 文本编码器
3. State Encoder：MLP 编码机器人末端位姿（6D）和夹爪状态（二进制）

Token 序列构造：

首先，所有模态的嵌入（图像、语言、状态）都通过线性变换映射到同一维度 $d$，然后将所有模态的 Token 拼接成一个序列。

视频生成预训练时：

$$\text{Input Tokens} = \underbrace{[l]}_{\text{语言}} \underbrace{[o_{t-h}]}_{\text{图像}} \underbrace{[\text{OBS}]}_{\text{视频预测 cls}} \oplus \cdots \oplus [l][o_t][\text{OBS}]$$

使用机器人数据微调时：

$$\text{Input Tokens} = \underbrace{[l]}_{\text{语言}} \underbrace{[s_{t-h}]}_{\text{状态}} \underbrace{[o_{t-h}]}_{\text{图像}} \underbrace{[\text{OBS}]}_{\text{视频预测 cls }} \underbrace{[\text{ACT}]}_{\text{动作预测 cls}} \oplus \cdots \oplus [l][s_t][o_t][\text{OBS}][\text{ACT}]$$

1. 模态对齐：语言 Token $l$ 在每个时间步重复，防止被其他模态掩盖
2. 因果注意力掩码：只能往前看，不能往后看
   • 预训练时掩码未来 $\text{[OBS]}$ Token
   • 微调时同时掩码 $\text{[OBS]}$ 和 $\text{[ACT]}$ Token
3. 时间嵌入：每个时间步添加可学习的时间戳编码

训练流程#

预训练阶段（视频生成）#

输入：语言描述 + 历史帧序列

输出：未来帧预测（MSE 损失，和 MAE 重构损失一样，直接就是判断像素差）

$$\mathcal{L}_{\text{video}} = \frac{1}{H \times W} \sum_{i=1}^H \sum_{j=1}^W \left( \hat{o}_{t+\Delta t}(i,j) - o_{t+\Delta t}(i,j) \right)^2$$

• $\hat{o}_{t+\Delta t}$：预测的未来帧
• $o_{t+\Delta t}$：真实的未来帧

微调阶段（机器人操作）#

输入：语言指令 + 历史状态 / 图像序列

输出：动作（连续位移 + 夹爪开合） + 未来帧预测

动作损失（Smooth L1）：

$$\mathcal{L}_{\text{arm}} = \frac{1}{N} \sum_{i=1}^N \begin{cases} 0.5 (a_{\text{arm}}^i - \hat{a}_{\text{arm}}^i)^2, & \text{if } |a_{\text{arm}}^i - \hat{a}_{\text{arm}}^i| < 1 \\ |a_{\text{arm}}^i - \hat{a}_{\text{arm}}^i| - 0.5, & \text{otherwise} \end{cases}$$

• $N$：批量大小（Batch Size）
• $a_{\text{arm}}$：真实动作，$\hat{a}_{\text{arm}}$：预测动作，就是位移和旋转那六个自由度的数值

Smooth L1 Loss 是回归任务中常用的损失函数，结合了 L1 Loss 和 L2 Loss 的优点。其公式为：

$$\text{SmoothL1}(x) = \begin{cases} 0.5x^2 & \text{当 } |x| < 1 \\ |x| - 0.5 & \text{其他情况} \end{cases}$$

其中 $x = y_{\text{pred}} - y_{\text{true}}$ 表示预测值与真实值的差。

特点：

1. 在 $|x| < 1$ 时使用二次函数（类似 L2 Loss），梯度平缓，避免离群值梯度爆炸；
2. 在 $|x| \geq 1$ 时使用线性函数（类似 L1 Loss），降低大误差时的梯度幅值；
3. 在 $x=0$ 处可导，优化更稳定。

夹爪动作损失（Binary Cross-Entropy）：

$$\mathcal{L}_{\text{gripper}} = -\frac{1}{N} \sum_{i=1}^N \left[ y_i \log p_i + (1 - y_i) \log (1 - p_i) \right]$$

• $y_i$：真实标签（0 或 1）
• $p_i$：预测为张开状态的概率

总损失：

$$\mathcal{L}_{\text{finetune}} = \mathcal{L}_{\text{arm}} + \mathcal{L}_{\text{gripper}} + \mathcal{L}_{\text{video}}$$

TinyVLA#

Paper ↗ / Project Homepage ↗

Insight#

1. 传统 VLA 模型依赖大型 VLM + AR，速度慢、推理延迟高
2. 数据依赖问题

Method#

1. 使用小型 VLM Backbone
2. 冻结预训练权重，仅微调部分参数（LoRA），保留多模态理解能力，减少数据依赖
3. 使用扩散策略头来生成最终动作，以多模态主干输出的嵌入（图像 + 语言指令）作为扩散过程的控制条件

DiffusionVLA#

Paper ↗

没看懂他的 FiLM 注入模块是如何实现的。

推理标记通过 FiLM 层注入策略模型，FiLM 层对策略内部投影层的参数进行缩放和偏移。

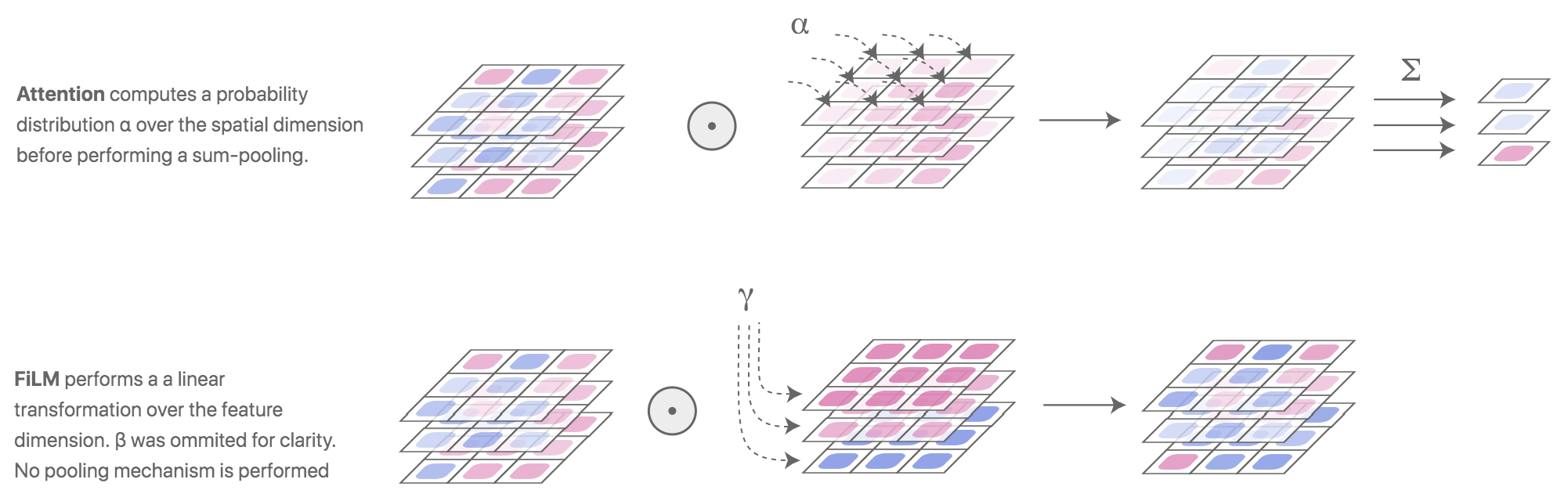
Reference ↗

CogACT#

Paper ↗

Condition and Action

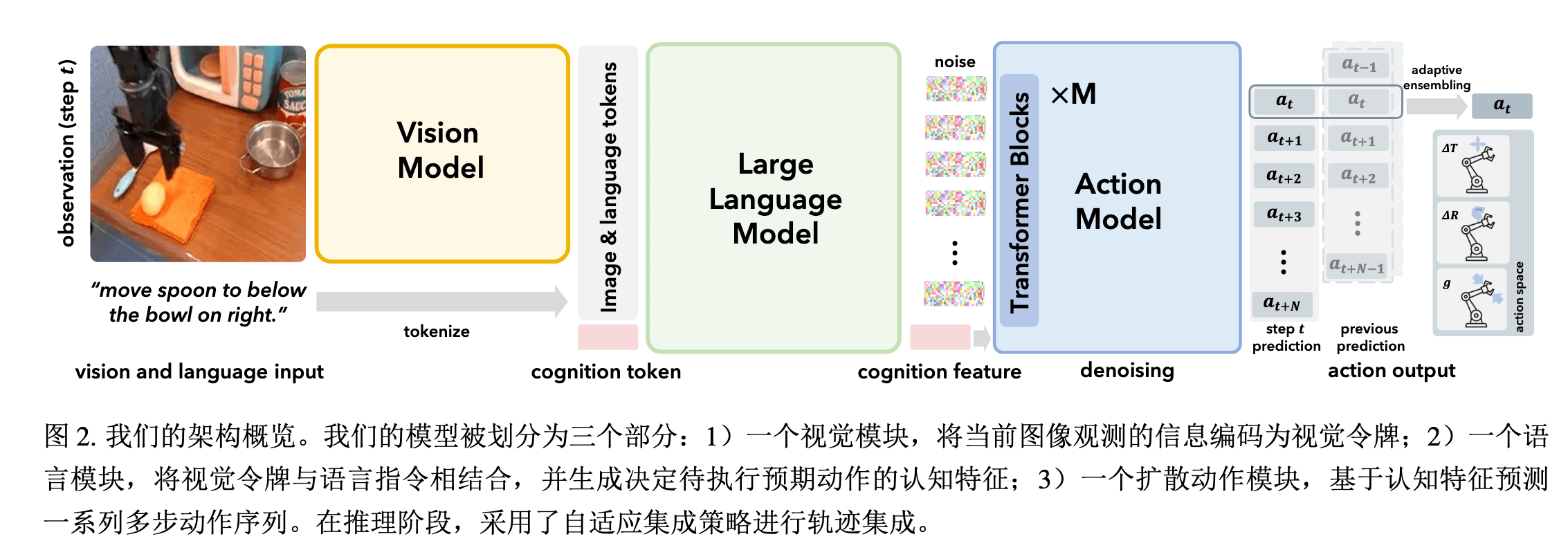
Insight#

1. VLM 直接将动作离散化为 Token 预测，忽略了动作的连续性和多模态性，导致成功率差、精度低
2. 动作信号具有连续性、多模态性（同一任务有多个可行轨迹）、时序相关性，与语义 Token 有本质不同
3. 模仿人脑功能划分，用 VLM 处理认知（理解任务），DiT 处理动作生成

Method#

Arch#

Backbone：

1. Vision Encoder：DINOv2 + SigLIP
2. LLM：LLaMA-2 7B
3. Action：DiT

整体 Token 序列结构：

$$\text{Input Tokens} = \underbrace{[V_1,...,V_{N_v}]}_{\text{视觉}} \oplus \underbrace{[L_1,...,L_{N_l}]}_{\text{语言}} \oplus \underbrace{[C]}_{\text{认知}}$$

使用因果注意力机制聚合信息后，得到认知特征 $f_t^c \in \mathbb{R}^{d_c}$。

$f_t^c, (a_t^i, a_{t+1}^i, ..., a_{t+N}^i)$ 作为动作模块的条件，进行条件扩散生成。

也即，训练网络学会从带噪声（人为加噪）的动作序列 $(a_t^i, a_{t+1}^i, ..., a_{t+N}^i)$ 中恢复出干净的动作序列 $(a_t, a_{t+1}, ..., a_{t+N})$。

其中：

• 符号 $i$ 表示去噪步骤的索引，会通过位置编码加入到认知特征 $f_t^c$ 中
• $t$ 表示时间步

Loss function#

$$\mathcal{L}_{\text{MSE}} = \mathbb{E}||\boldsymbol{\hat{\epsilon}}^i - \boldsymbol{\epsilon}||_2$$

其中：

• $\boldsymbol{\epsilon}$：扩散过程添加的高斯噪声
• $\boldsymbol{\hat{\epsilon}}^i$：第 i 步去噪时预测的噪声

扩散模型通过预测噪声间接建模动作分布，避免直接回归的模态坍缩问题。

AAE (Adaptive Action Ensemble)#

可以看到，我们每步根据观测信息最终会预测一个 Action Chunk，但推理的时候它们会彼此重叠，没有充分利用信息；而如果每个时间步都只用 Action Chunk 的最开始一部分，又会导致动作不平滑。

为此，作者提出了一种自适应动作聚合的方式，通过余弦相似度来为不同时间步预测的同一时刻的动作进行加权：

$$\hat{\boldsymbol{a}}_t = \sum_{k=0}^{K} w^{\text{ada}}_k \cdot \boldsymbol{a}_{t}|\boldsymbol{o}_{t-k}$$

其中：

• $\hat{\boldsymbol{a}}_t$：最终预测的动作
• $w^{\text{ada}}_k$：加权系数
• $\boldsymbol{a}_{t}|\boldsymbol{o}_{t-k}$：第 $t-k$ 步预测的第 $t$ 步动作
• $\boldsymbol{o}_{t-k}$：第 $t-k$ 步的观测信息
• $K$：采用最近几次的历史动作预测，基于训练集动作的标准偏差来确定

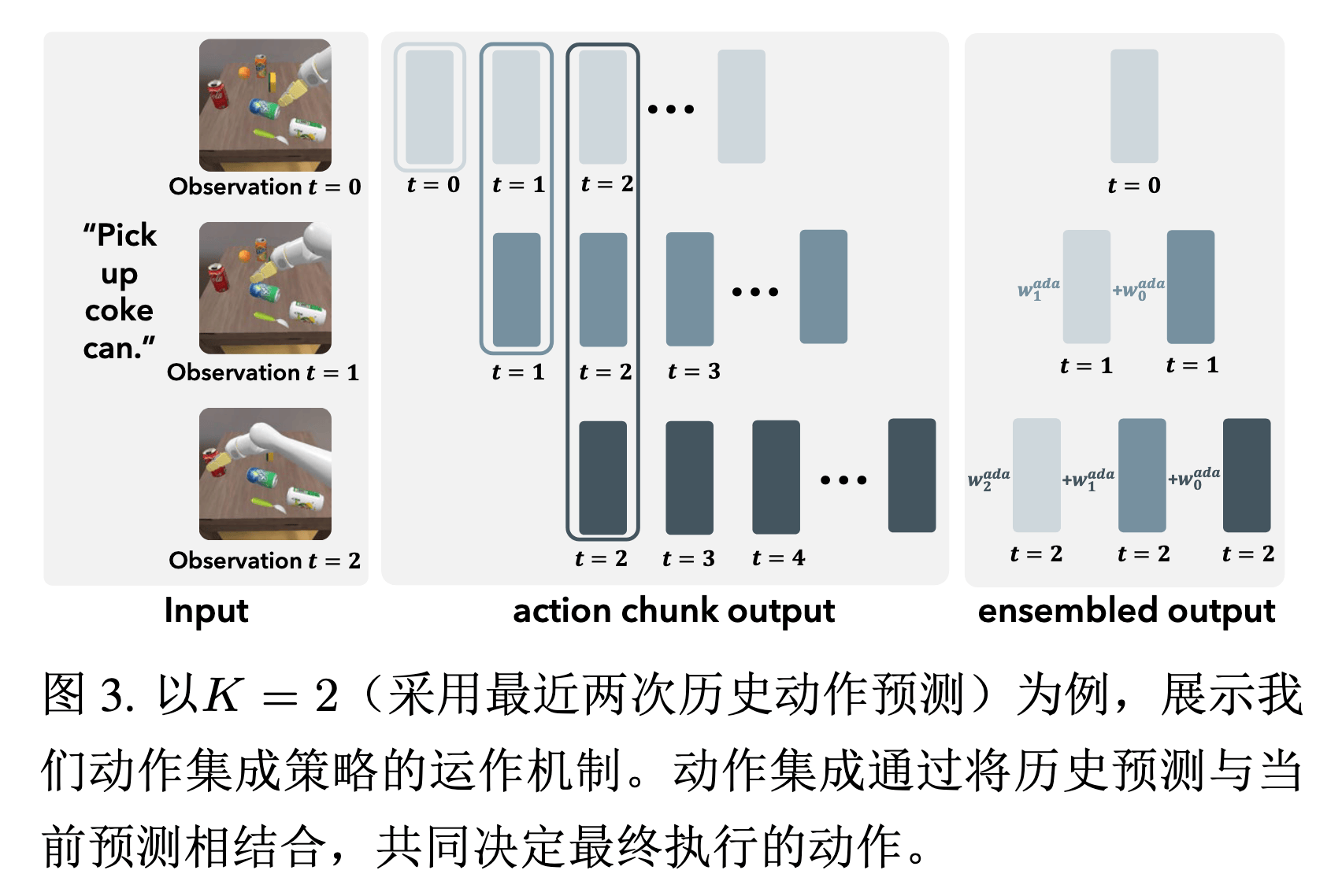
加权系数的计算方式：

$$w_k^{\text{ada}} = \exp(\alpha \cdot \langle \boldsymbol{a}_t|\boldsymbol{o}_t, \boldsymbol{a}_t|\boldsymbol{o}_{t-k} \rangle)$$

• $\langle \cdot,\cdot \rangle$：余弦相似度（取值范围 $[-1,1]$）
• $\alpha$：温度系数，超参数
• $\boldsymbol{a}_t|\boldsymbol{o}_{t-k}$：基于历史观测 $\boldsymbol{o}_{t-k}$ 预测的当前时刻动作

实际使用时会进行 softmax 归一化：

$$\hat{w}_k = \frac{w_k^{\text{ada}}}{\sum_{j=0}^K w_j^{\text{ada}}}$$

本质就是 相似度越高 → 权重越大，从而保留相同动作模式，并且实现平滑过渡。

PointVLA#

Paper ↗

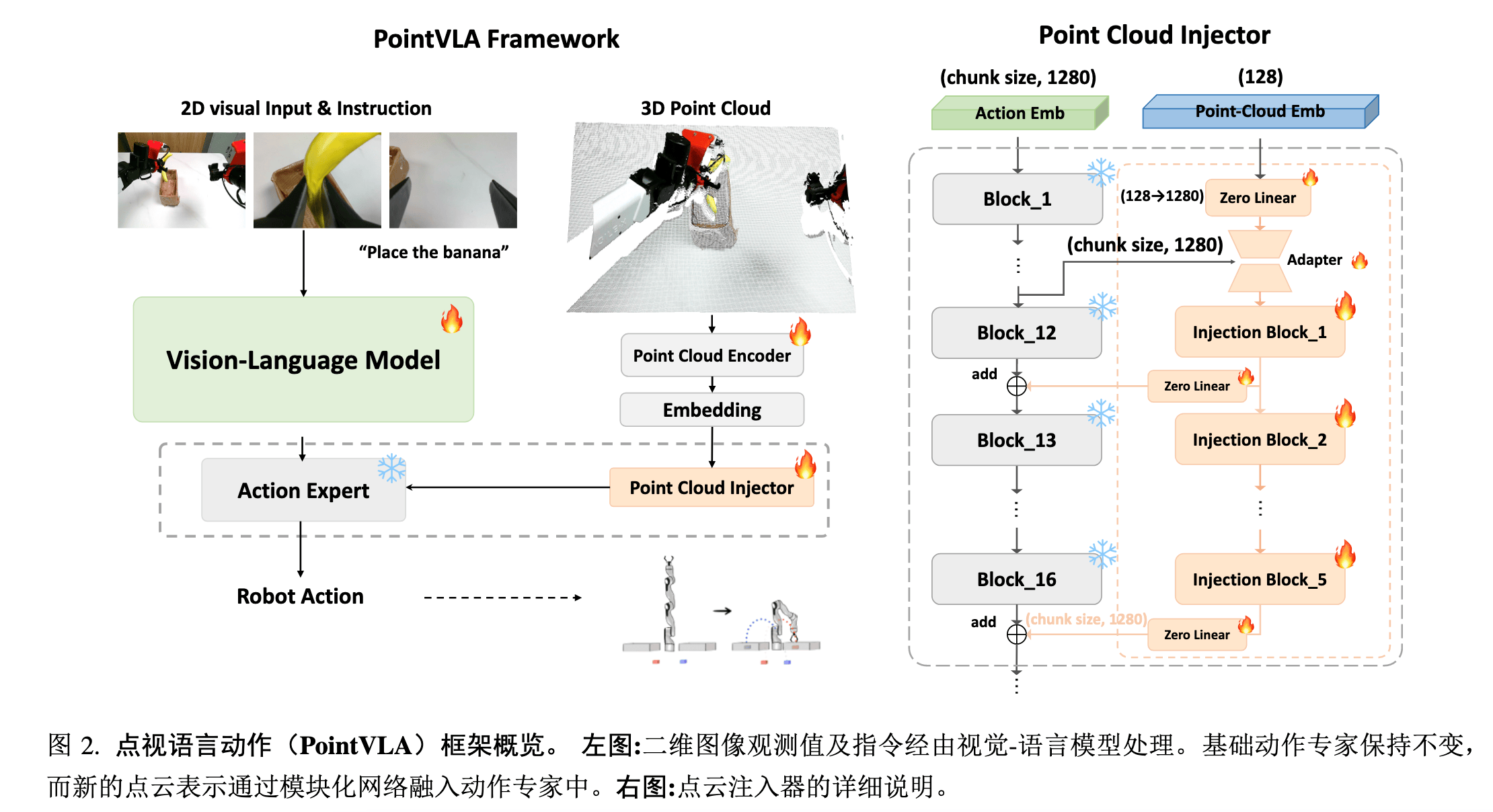
Insight#

• 现有 VLA 模型（如 OpenVLA、DexVLA）依赖 2D 图像输入，难以处理需要深度感知的任务；重新训练包含 3D 数据的 VLA 模型成本高昂，而丢弃已有的大规模 2D 数据集会造成资源浪费
• 所以，选择将 3D 点云信息嵌入后注入动作专家模块，然而直接微调 VLM 主干会引发灾难性遗忘，不加选择的注入动作专家模块也会引发性能暴跌
• 通过这种方式，作者实现了不破坏预训练 VLA，同时高效融合 3D 点云信息

Method#

Arch#

Backbone：

• VLM：Qwen2-VL，2B
• Action：ScaleDP，1B，Diffusion 变体

3D injector：在选定层执行 $h_{\text{new}} = h_{\text{2D}} + \text{MLP}(f_{\text{3D}})$，其中 $h_{\text{2D}}$ 为原动作专家选定的几个层的隐藏状态。

这里 $f_{\text{3D}}$ 有一个分层卷积设计，而且是从头开始训练的。作者发现，预训练的 3D 视觉编码器会阻碍性能，往往在新环境中难以成功学习机器人行为。

Skip-Block#

由于要额外引入 3D 注入，所以作者探究了一下在动作专家模块中模块对性能的影响，从而选择影响较小的层去注入信息（这个思想类似于模型剪枝的时候的操作）。

作者发现，动作专家模块的前 11 层影响很大，后续层则可以进行替换或注入，这比较符合直接，前期对 2D 及语义特征的处理还相对低级，自然会比较重要，对性能影响大。

DexVLA#

Paper ↗

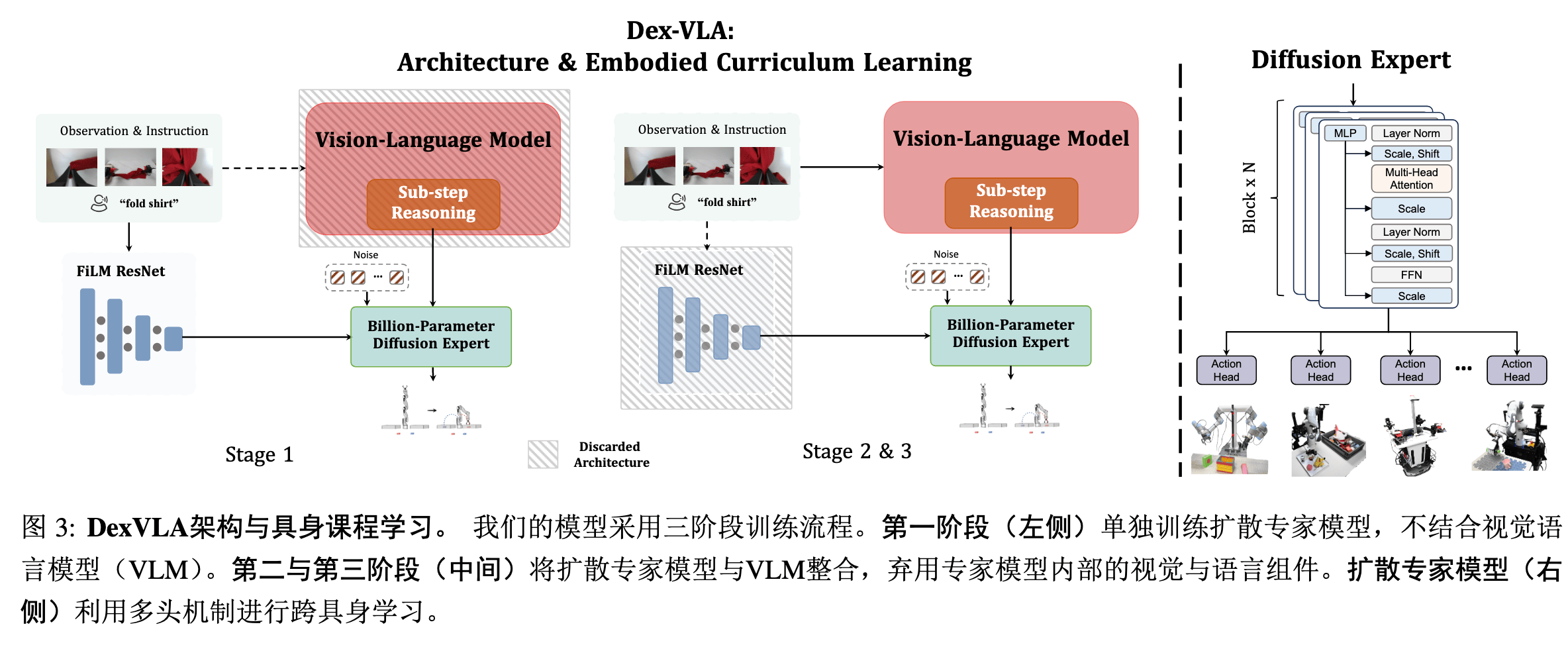
Insight#

• 之前的 VLA 明显在 LLM 和 Action 部分大小失衡，过度扩展视觉语言模块（VLM 参数达 3B-7B），而动作专家部分（action expert）仍停留在百万参数级别，成为性能瓶颈

Method#

Arch#

Backbone：

• VLM：Qwen2-VL，2B
• Action：ScaleDP，1B，Diffusion 变体，具有多个策略头，可以适配多种不同的下游机型

Training#

很怪的训练方法，分阶段训练不是没见过，但都是整体 pipeline 不变，只改变冻结部分的，本文的训练在不同阶段的 pipeline 都变了，前一阶段用的部分再后续阶段直接丢掉了。

1. 阶段 1：仅用跨形态数据预训练动作专家，也就是扩散部分，学习低级运动技能（如抓取、移动）。语义部分 不是靠 VLM，而是暂时性靠另外一个 ViT/DistilBERT 编码，随后经过 FiLM+ResNet 来进行整合，送入扩散部分。
2. 阶段 2：绑定 VLM 与动作专家，冻结 VLM 的视觉编码器，联合训练视觉到 Token 的投影层以及扩散专家，用特定形态数据对齐视觉 - 语言 - 动作映射。舍弃上一阶段的 FiLM+ResNet 不分。
3. 阶段 3：全模型微调，微调时引入 高质量子步骤推理标注数据，使模型能自动分解长期任务（如 “叠衣服” 分解为展平、对齐袖子等）。