ViT、BEiT、iBOT、MAE

Visual Transformer

• 将标准 Transformer 迁移到 CV 任务上，尽可能少的做修改
• 不引入 CNN 作为前置网络，因为这样会造成归纳偏置（局部性、平移等变性）
• 将图片等分地划分为很多 patches，每个 patches 越小则计算量越大（序列长度越大），注意 Transformer 的计算复杂度是 序列长度 $n$ 的平方 $\mathcal{O}(n^2)$

BEiT

简介

• 迁移 BERT 到视觉任务
• 模型学习恢复原图像的 视觉令牌，而不是遮蔽块的原始像素

如何理解嵌入 / 令牌：图像具有很高的维度，但是并不是所有维度都是有用的（乱码图片），有些维度是冗余的，有些维度是有用的。令牌就是对图像的有用信息的一种抽象表示。通过将图像从高维像素空间映射（也就是嵌入）到（相对低维的）令牌空间，可以更好地捕捉图像的语义信息。并满足一些诸如相似者近、支持语义操作的特点。

dVAE

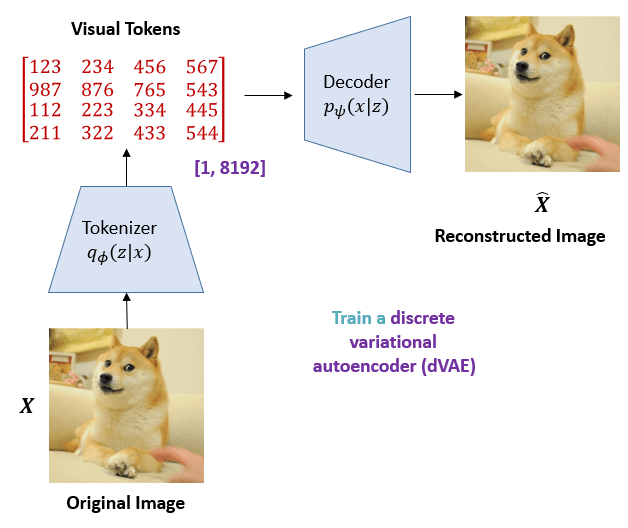
Tokenizer / Encoder

• 首先切出 patch，并展平

• 根据距离最近原则找到各个 patch 的离散 Token（Gumbel-softmax），加上位置嵌入与 cls 标记，cls 标记以 $\boldsymbol{e}_{[S]}$ 表示，$\boldsymbol{E}$ 是嵌入矩阵。cls 标记用于学习全局特征后，预测图像级别的标签，如分类任务。

  $$\boldsymbol{H}_0=[\boldsymbol{e}_{[S]},\boldsymbol{E}x_i^p,\ldots,\boldsymbol{E}x_N^p]+\boldsymbol{E}_{pos}$$

• Transformer 块 L 个

• 输出图片的编码表示

Decoder

• 根据图片的编码表示重建图片

Loss

因为我们想要能够从嵌入编码得到的分布中重新采样、解码得到的图片具有随机性，所以为了防止退化成一对一的编码、解码（AutoEncoder），我们人为的限制（表示随机性的）方差不得退化为 0，也即引入先验假设 $p(Z)=N(0, I)$。通过要求均值方差拟合网络的输出 $p(Z|X)$ 与标准正态分布 $N(0, I)$ 尽可能接近。这样的话，我们就有

可以看到，在这个要求下，所得到的编码的分布也是一个正态分布，也就满足了我们的先验假设。

而这个过程，我们是通过引入额外的 KL 散度来实现的，也就是 ELBO 下界：

接下来根据重建误差与 KL 散度加和构成的损失函数，训练 Tokenizer：

训练过程

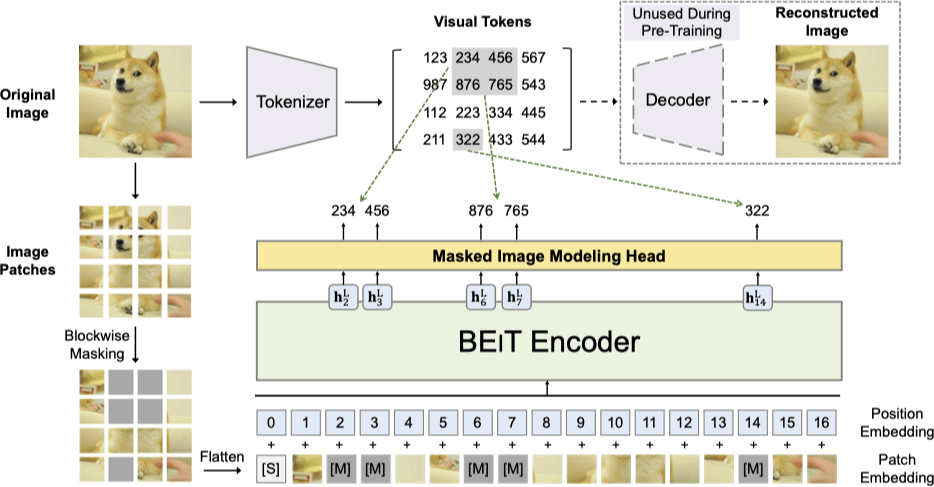
• 预训练 dVAE / Tokenzier
• 给定图片，切出 patches，通过预训练的 tokenizer（dVAE 里的 tokenizer 部分） 给出所有 patches 的 token
• 盖住一些 patches（通过对位替换为一个特殊的、可学习的编码 ${\boldsymbol{e}}_{[\mathrm{m}]}$），通过 BEiT Encoder 预测盖住的这些个 patch 的相应的 visual token
• 最大化对于盖住的 patches 输出真实 token 的概率

损失函数

dVAE

采用的是 ELBO 下界

• $x_i$: 原始输入图像。
• $\tilde{x}_i$: 对原始图像进行一些遮挡处理后的图像。
• $\mathcal{D}$: 数据集，包含训练数据对 $(x_i, \tilde{x}_i)$​​。

BEiT

总损失函数：

分为两个阶段：

Visual Token Reconstruction

• $q_\phi(z|x_i)$: 条件概率分布，表示给定原始图像 $x_i$ 时，隐变量 $z$ 的概率分布。这个部分是通过预训练的 tokenizer 获取的。
• $p_\psi(x_i|z_i)$: 条件概率分布，表示给定隐变量 $z_i$ 时，重建的原始图像 $x_i$ 的概率分布。

在这个阶段，目标是最大化重建的图像与原始图像之间的相似度，即通过最小化损失来进行训练 dVAE，尤其是其中的 Tokenizer

Masked Image Modeling

• $p_\theta(z|\tilde{x}_i)$: 条件概率分布，表示给定遮挡后的图像 $\tilde{x}_i$ 时，隐变量 $z$ 的概率分布。

这个阶段的目标是通过 BEiT Encoder 预测被遮挡的 patches 对应的 visual token。这里的损失主要通过预训练的模型预测真实 token 来进行最小化。

问题

重建会更关注高频细节、短范围依赖。

iBOT

简介

• 同一张图片经过不同的图像增强，仍应该具有相似的语义信息，所以采用
• student 作为目标网络，teacher 作为 tokenizer，tokenizer 和目标网络同步学习

训练过程

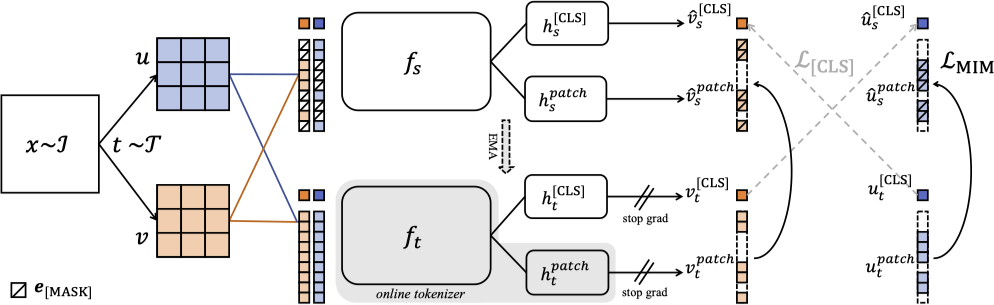
损失函数

自蒸馏

• 对于一张图片，不同的数据增强过后，经过两个网络得到的信息应当相近
• 为 $\texttt{[CLS]}$ 标签上的自蒸馏，不同的数据增强上交叉进行
• 目标是使学生网络的输出逼近教师网络的输出，提高预测一致性。

MIM

• $m_i$ 是掩码，用于只选择被 Mask 部分

• 为 patch 标签上的自蒸馏，同一数据增强上进行

• 计算同一张图片在老师 - 学生间重构的交叉熵，可以替换得到 $v$ 的对称化损失

• 使用 EMA + 学生模型的梯度（而不是老师模型自己的梯度），来更新老师模型

  

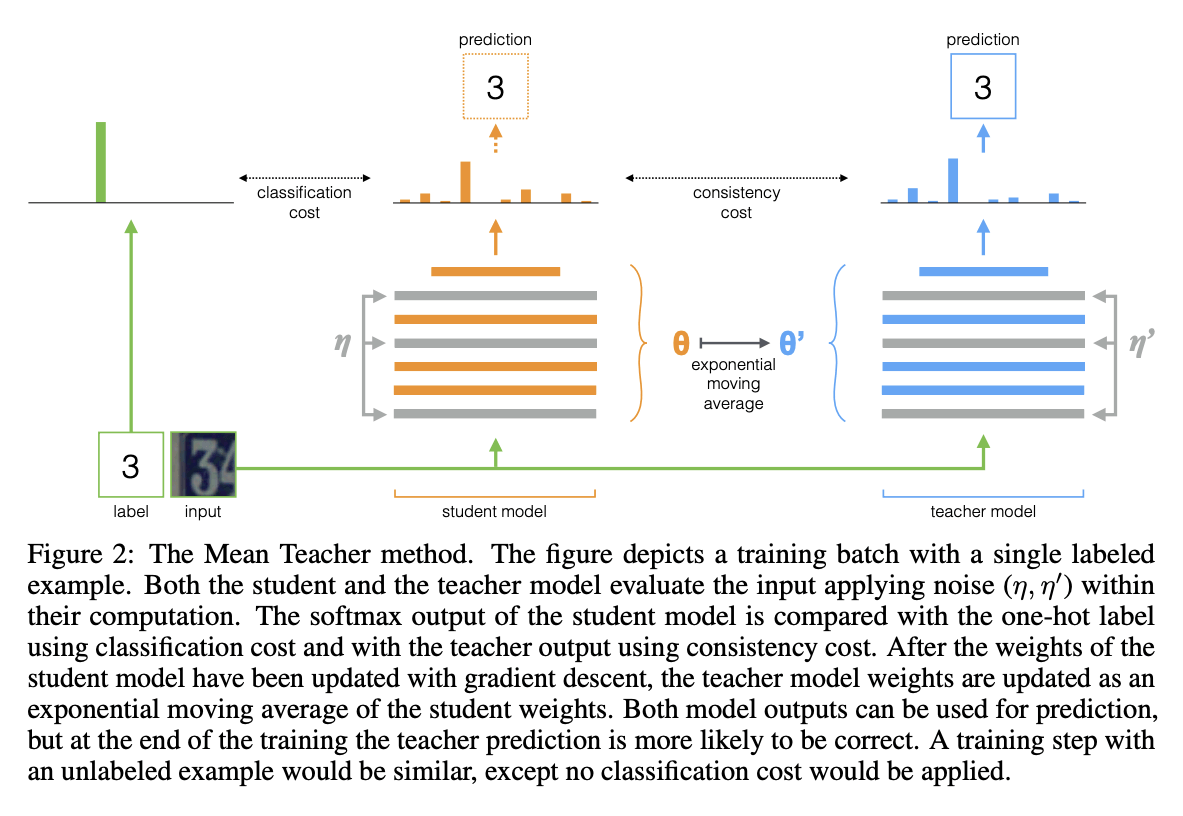
• 共享参数，可以得到更好的效果：

  $$h_s^{[\operatorname{CLS}]}=h_s^{\mathrm{patch}}\quad h_t^{[\operatorname{CLS}]}=h_t^{\mathrm{patch}}$$

伪代码

输入变量、初始化

• $g_s$ 和 $g_t$: 学生网络和教师网络，用于特征提取。
• $C, C'$: 分别是基于 $\texttt{[CLS]}$ token 和图像块（patch）tokens 的中心。
• $\tau_s, \tau_t$ 和 $\tau'_s, \tau'_t$: 分别是学生和教师网络在 $\texttt{[CLS]}$ token 和图像块（patch）tokens 上的温度参数，用于控制软标签的 “锐化” 程度。
• $l, m, m'$: 分别是网络、 $\texttt{[CLS]}$​ token 和图像块（patch）tokens 的动量更新率。
• 将教师网络的参数初始化为学生网络的参数，使其在开始时保持一致。

循环

1. 数据加载和增强
   • 通过数据加载器循环遍历数据，每次处理一个批次的数据 $x$。
   • 对每个数据点 $x$ 进行两次随机视图生成（augment），得到 $u$ 和 $v$。
2. 遮蔽操作
   • 对 $u$ 和 $v$ 进行随机的块状遮蔽，生成 $\hat u$ 和 $\hat v$，同时记录遮蔽的位置 $m_u$ 和 $m_v$。
3. 特征提取
   • 使用学生网络 $g_s$ 和教师网络 $g_t$ 处理遮蔽后和未遮蔽的视图，提取 $\texttt{[CLS]}$ token 和图像块（patch）tokens 的特征。
4. 损失函数计算
   • $\mathcal{L}_\texttt{[CLS]}$ 计算学生和教师网络输出的 $\texttt{[CLS]}$ token 特征之间的差异。
   • $\mathcal{L}_\mathrm{MIM}$ 计算图像块（patch）tokens 特征之间的差异，其中只有遮蔽的部分参与计算。
5. 反向传播和参数更新
   • 计算总损失并执行反向传播。
   • 更新学生网络的参数，并根据动量率更新教师网络的参数。
   • 更新中心 $C$ 和 $C'$​，使用动量平均策略。

辅助函数 $\mathrm{H}$

• 计算两组特征之间的信息熵损失。这个函数首先停止梯度传递到 $t$
• 对 $s$ 和 $t$​ 应用 softmax 操作进行归一化，然后计算交叉熵。

问题

• 如何更好的理解 EMA 以及蒸馏的过程，为什么老师的输出可能更好？

MAE

训练过程

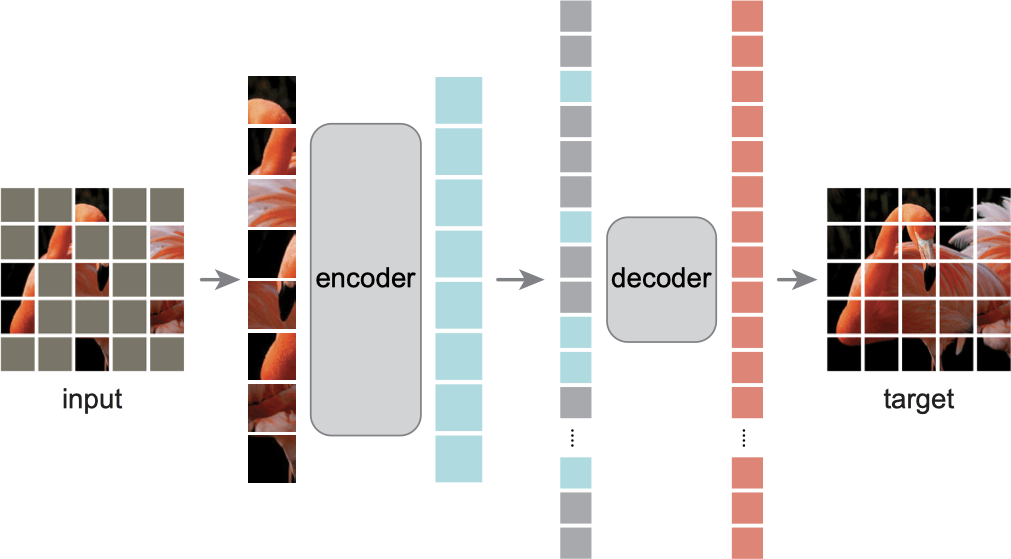
• 首先对图片切出 patches，然后随机掩蔽（通过打乱后取前面一部分来实现），只取没被掩蔽的部分输入 encoder，尝试得到具有语义信息的 token
• 通过一个全连接层适配到 decoder_embed，然后依照顺序插入 [Mask]
• 使用 decoder 恢复到像素空间，使用 MSE 计算损失

Credit

• Lilian / From Autoencoder to Beta-VAE
• 科技猛兽 / Self-Supervised Learning 超详细解读 (三)：BEiT：视觉 BERT 预训练模型
• LLM-Finder / 以史为鉴！EMA 在机器学习中的应用
• 科技猛兽 / Self-Supervised Learning 超详细解读 (七)：大规模预训练 Image BERT 模型：iBOT