基础概念#
连杆(Link):按照顺序连接的刚体。
关节(Joint):连接连杆的部件,决定了相邻连杆之间的运动自由度(DoF,Degree of Freedom)。
自由度(DoF,Degree of Freedom):机械臂的自由度是指机械臂能够自由运动的维度。
点的表示与坐标系#
约定:
- 任意点 p 的位置由一个参考系 Fs 记录。
- 点的坐标记为普通字母(如 p),向量用粗体字母表示(如 v)。
- s 代表 space,b 代表 body。
记录公式包含参考系的上标,例如:

obs=oss+ts→bs
这个公式表示:在坐标系 Fs 中,点 ob 的位置是 os 的位置加上平移向量 ts→bs。
刚体的位姿变换#
刚体自身会绑定一个坐标系 Fb,当刚体移动时,此坐标系也会移动。
所以,刚体的 位姿(位置与姿态,pose) 变化,就是通过 坐标系变换 来对齐两个坐标系。也即将 Fs 通过旋转和平移变换,使其与 Fb 重合。
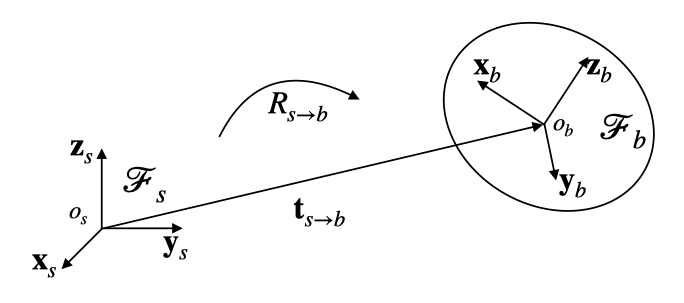
- 转动矩阵(rotation):Rs→b,用于对齐坐标轴 {xi,yi,zi},代表 “朝向”
- 平动向量(translation):ts→b,用于对齐原点 os 和 ob,代表 “位置”
(Rs→bs,ts→bs) 合在一起,就描述了一个刚体的位姿,其拥有 6 个自由度,转动和平动各自拥有 3 个自由度。
- 原点变换:
obs=oss+ts→bs
- 坐标轴变换:
[xbs,ybs,zbs]=Rs→b[xss,yss,zss]
如果观察者使用 Fs:
oss=0,[xss,yss,zss]=I3×3
则:
ts→bs=obs,Rs→b=[xbs,ybs,zbs]∈R3×3
相对的,如果观察者使用 Fb:
假设刚体上的点 p 在 Fb 中的坐标为 pb(随刚体运动,所以相对于坐标系 Fb 固定不变),其在 Fs 中的坐标为 ps,则有:
- 初始时,Fs=Fb,ps=pb。
- 刚体发生运动,相对于参考系 Fs,此运动可以描述为 (Rs→bs,ts→bs),则:
ps=Rs→bspb+ts→bs
- 同理,对于任意点 xs,变换后的点 x′s 表示为:
x′s=Rs→bxs+ts→b
值得注意的是,当 ts→bs=0 时, (Rs→bs,ts→bs) 这个变换并不是线性的。反之,当 ts→bs=0 时,变换是线性的。
齐次坐标#
在三维空间中,齐次坐标系将一个点 x∈R3 表示为:
x~:=[x1]∈R4
对应的,齐次变换矩阵具有以下形式:
Ts→bs=[Rs→bs0ts→bs1]
其中 Rs→bs 是旋转矩阵,ts→bs 是平移向量。
这么做的原因是,在传统的笛卡尔坐标系中,平移和旋转是两种不同性质的变换:
- 旋转是线性变换:x′=Rx
- 平移是仿射变换:x′=x+t
这导致无法用单一矩阵乘法表示同时包含旋转和平移的变换。而在齐次坐标系中,两种变换统一为:
[x′1]=[R0t1][x1]=[Rx+t1]
注意,这种变换保持刚体的形状和大小不变,只改变其位置和方向。
通过引入齐次坐标,我们恢复了线性,此时多个变换的组合可以通过矩阵乘法简洁表示,且满足传递性、可逆性:
T3=T2⋅T1T2→12=(T1→21)−1
这极大地简化了计算复杂变换序列的过程,现在,坐标变换遵循一般规则:
x1=T1→21x2
直观上容易记混淆这个公式。请记住,这个 x 是随着刚体变动的,x2 是其在变换后坐标系下的坐标,亦是变换前的坐标,经过固定坐标系下的变换矩阵 T1→21 ,就得到了变换后的、在原始固定坐标系下的坐标 x1。
同时,我们显然有:
x2=(T1→21)−1x1=T2→12x1
在后文中,我们忽略 ~ ,默认在齐次坐标系下写公式。
多连杆刚体几何#
基本关节类型#
-
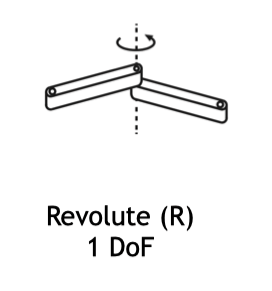
Revolute Joint(旋转关节 / 铰链关节)
-
允许绕单一轴线的旋转运动。
-
1 DoF
-
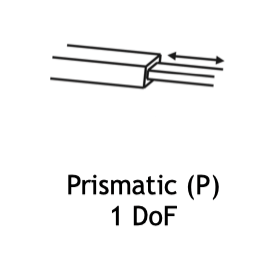
Prismatic Joint(滑动关节 / 平移关节)
-
允许沿单一方向的平移运动。
-
1 DoF
-
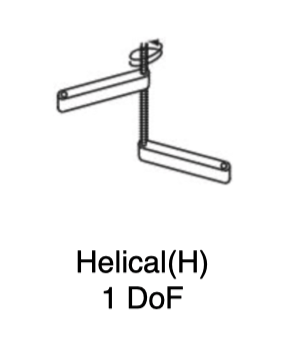
Helical Joint(螺旋关节)
-
Spherical Joint(球形关节 / 球窝关节)
-
允许绕球心进行任意方向的旋转。
-
3 DoF
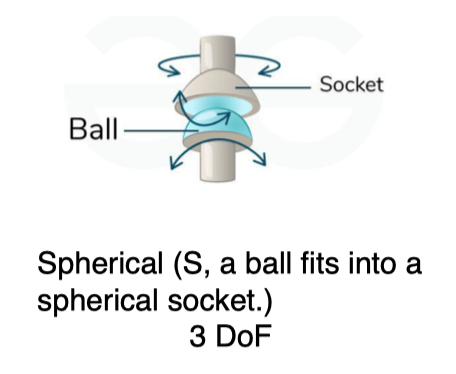
总结:
| 关节类型 | 英文名称 | 自由度(DoF) | 运动描述 |
|---|
| 旋转关节 | Revolute (R) | 1 | 绕单一轴线旋转 |
| 滑动关节 | Prismatic (P) | 1 | 沿单一方向平移 |
| 螺旋关节 | Helical (H) | 1 | 螺旋运动(旋转 + 平移) |
| 球形关节 | Spherical (S) | 3 | 任意方向旋转 |
基座连杆和末端执行器#
基座连杆 (Base link / Root link)#
- 定义:第 0 号连杆。
- 特点:
- 被视为 “固定” 参考。
- 空间坐标系 Fs 附着于此。
末端执行器连杆 (End-effector link)#
- 定义:最后一个连杆。
- 特点:
- 通常为抓手(gripper)。
- 末端坐标系 Fe 附着于此。
如何看坐标系:
- x 是红
- y 是绿
- z 是蓝
变换矩阵#
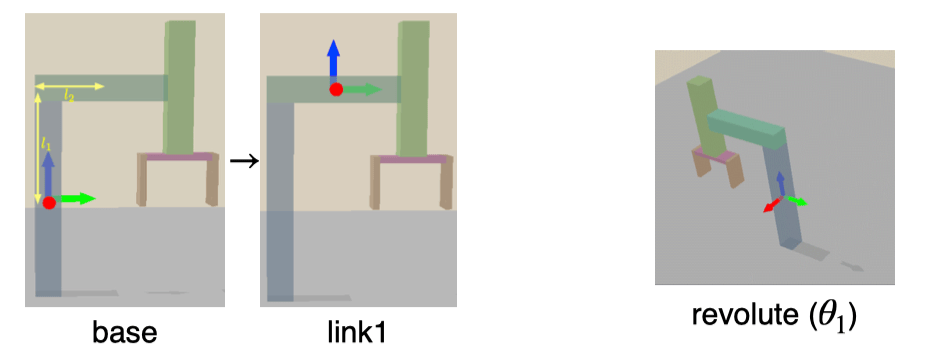
T0→10=cosθ1sinθ100−sinθ1cosθ1000010−l2sinθ1l2cosθ1l11
要点:旋转矩阵没影响 z 轴;平动向量在平面上也有变动,因为绕着 l2 左端点转了一下。
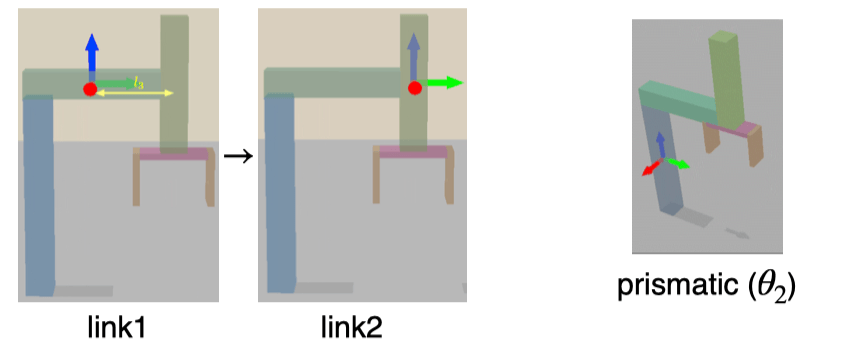
T1→21=1000010000100l3θ21
要点:转动矩阵为 I;平动向量只改了 y,z。
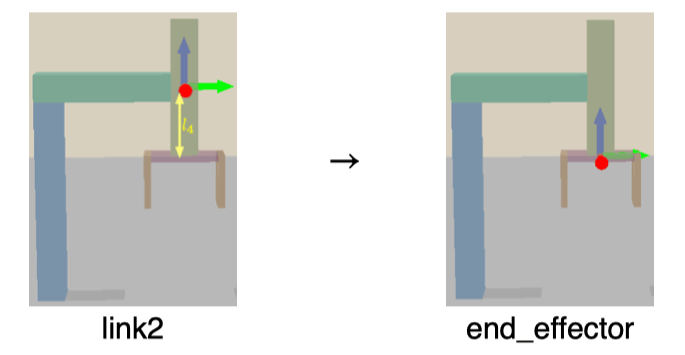
T2→32=10000100001000−l41
要点:转动矩阵为 I;平动向量只改了 z。
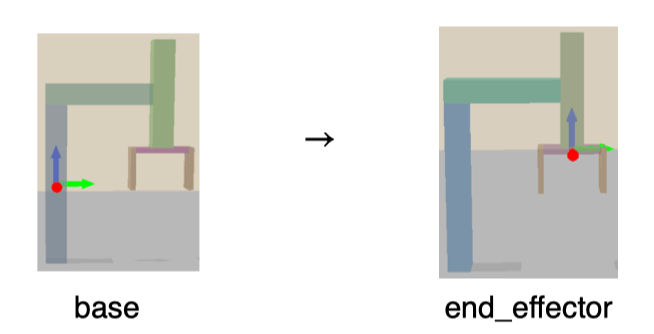
T0→30=T0→10T1→21T2→32=cosθ1sinθ100−sinθ1cosθ1000010−sinθ1(l2+l3)cosθ1(l2+l3)l1−l4+θ21=[Rs→es0ts→es1]
旋转的参数化#
参数化:用一组简单的数值参数来完整描述一个复杂系统或对象的过程。
假设我们已经为 Robot 的每个连杆(Link)分配了坐标系,那么我们可以使用相邻(adjacent)坐标系之间的 相对角度 和 平移 来参数化每个关节。
而对于末端执行器(End-Effector),我们又有如下两种方式来表征其位姿:
关节空间表示(Joint space)#
- 这是一个向量空间,其中每个坐标是关节位姿的向量
- 具体来说,是关节围绕关节轴的 角度 向量
- 例如,一个 6 自由度机器人会有 6 个关节角度值 (θ1,θ2,θ3,θ4,θ5,θ6)
笛卡尔空间表示(Cartesian space)#
- 这是末端执行器刚体变换的空间
- 用数学符号表示为:(Rs→e,ts→e)
- 其中 Rs→e 表示从基座坐标系到末端执行器坐标系的旋转矩阵
- ts→e 表示从基座坐标系到末端执行器坐标系的平移向量
- Fe 表示末端执行器的坐标系
- 关节空间 直观地反映了机器人各关节的实际物理状态,强调关节。
- 笛卡尔空间 则描述了机器人末端在三维空间中的实际位置和方向,更符合人类思考方式,容易进行判断目标是否达成,强调末态。
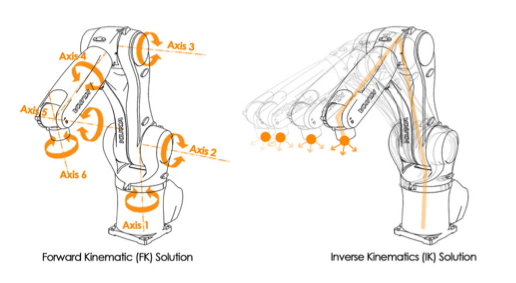
正向运动学 (Forward Kinematics,FK)#
正向运动学将关节空间坐标 θ∈Rn 映射到变换矩阵 T:
Ts→e=f(θ)
也即,给定关节角度,计算末端执行器的位置和姿态。
这一映射可以简单地通过沿着运动链组合各个变换矩阵计算得出。
逆向运动学 (Inverse Kinematics,IK)#
逆向运动学解决的问题:给定正向运动学 Ts→e(θ) 和目标姿态 Ttarget=SE(3),求解满足以下条件的关节角度 θ:
Ts→e(θ)=Ttarget
过程:给定末端执行器的目标位置和姿态,计算需要的关节角度
逆向运动学比正向运动学更复杂,因为 T−1 可能很难计算,所以 通常可能有多个解或无解。

根据前文所述,三维空间中,任何刚体的完整位姿可以用 6 个独立参数完全描述,即 (R,t)。
因此,6 自由度是机械臂实现空间中任意位置和姿态所需的最小自由度数量。这也称为 “完全自由度” 配置。
至少 6 个自由度可以保证覆盖此空间,从而 IK 的方程有解(但有时候可能得不到解析解,只能得到数值解)。
引理:如果机械臂构型满足 Pieper Criterion,则有解析解(闭式解)。
实例:UR5 机械臂。
虽然 6 自由度保证了有解,但是这个解可能超出了可行空间(如碰撞解),所以额外增加 1 个冗余自由度形成 7 自由度,可以扩大解空间,更有可能找到可行解(非碰撞解)。
但我们不能一味增加自由度,因为这会带来工程复杂性并延长反应时间,所以目前工业界一般是 6 或者 7 DoF。
一个 IK 求解方式(cuRobo):
-
选定一个初始值 θ0
-
目标:最小化能量函数(Energy Function)
argθmin∣∣Ts→e(θ)−Ttarget∣∣2
-
迭代直到收敛
-
可以使用 GPU 并行迭代多个随机选定的初始值,加快速度,并尝试找到最优解
假设我们已知机械臂现在状态,我们想要略微移动一点到达新的状态,我们该选择何种表征进行预测?
- 使用笛卡尔空间,优点是 (ΔR,Δt) 直观,容易预测,缺点是执行操作所需的 Δθ 难以计算(需要 IK),RT-2 选用的是这种。
- 使用关节空间,优点是预测得到 Δθ 后很容易操作,并计算移动后的 (R,t) 以及 (ΔR,Δt) 易于计算(FK),缺点是 Δθ 难以求解,π0 选用的是这种。
SE (3) 群与空间变换的表示方法#
SE (3) 是 Special Euclidean group in 3 dimensions 的缩写,代表三维特殊欧几里得群。它描述了三维空间中所有的刚体变换(rigid transformations),包括旋转和平移,但不包括缩放、切变等变形。
SE (3) 群可以数学表示为:
SE(3):={T=[R0t1],R∈SO(3),t∈R3}
其中:
- SO(3) 是三维特殊正交群,表示所有的三维旋转
- t 是三维空间中的平移向量
注意这里:
- 所有三维正交矩阵是 O(3)
- 旋转矩阵是 SO(3)⊂O(3),其满足行列式是 1,因为这样可以保证应用后手性不变,如果行列式是 -1,那么实际上是一个旋转加镜像的操作。
延伸:
- SO(2) 是二维旋转矩阵,有 1 个自由度
- SO(3) 是三维旋转矩阵,有 3 个自由度
欧拉角#
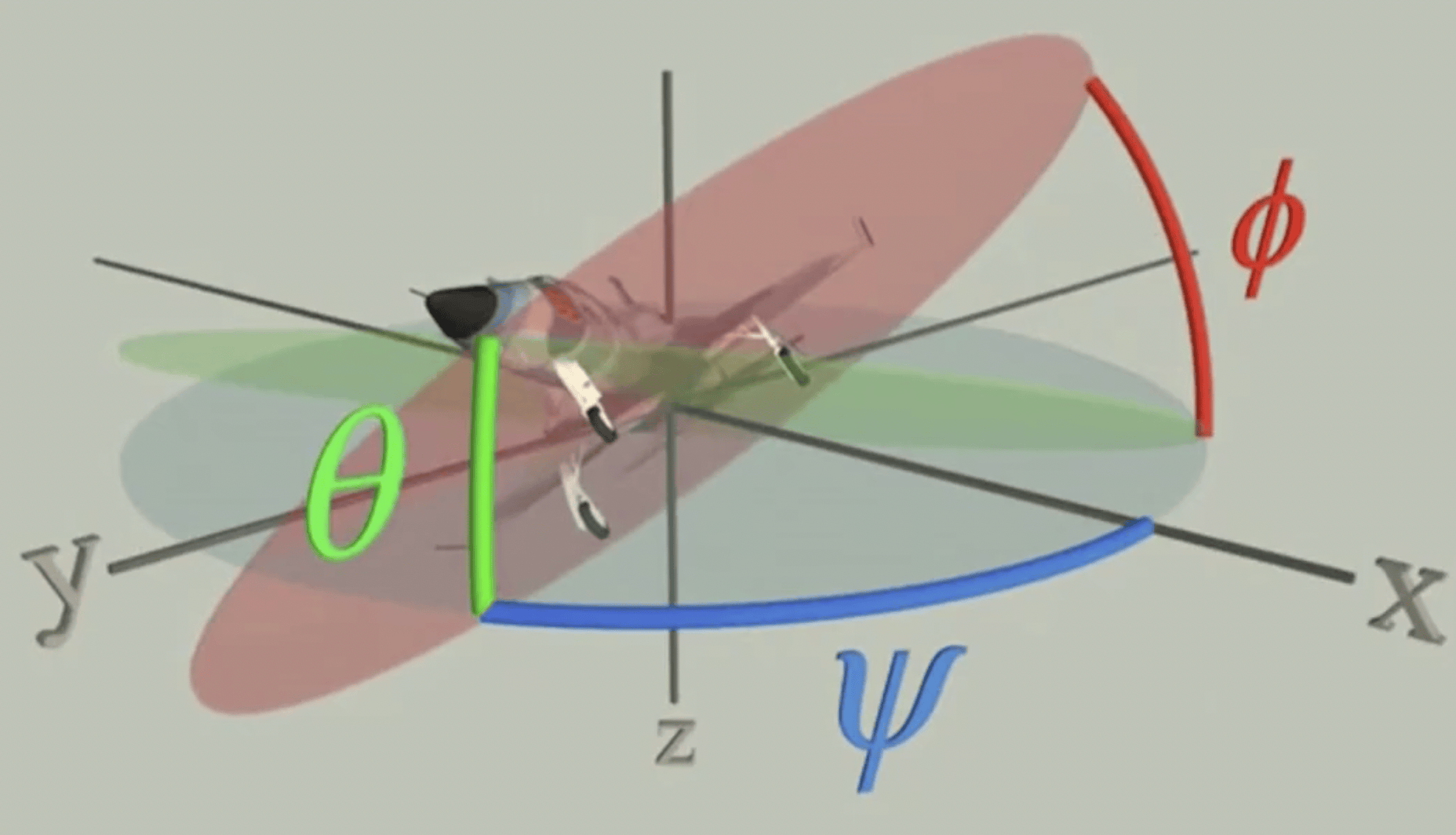
欧拉角(Euler Angles):描述三维旋转的一种方法,通过三个连续的旋转来表示任意旋转。
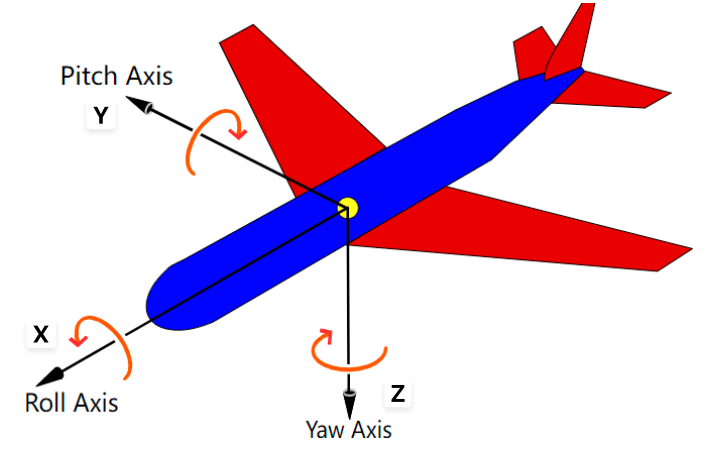
-
绕 X 轴旋转 ϕ(roll)

-
绕 Y 轴旋转 θ(pitch)

-
绕 Z 轴旋转 ψ(yaw)

应用:相较于旋转矩阵 R,所需数值表示从 9 个降低到了 3 个。
Rx(α):=1000cosαsinα0−sinαcosαRy(β):=cosβ0−sinβ010sinβ0cosβRz(γ):=cosγsinγ0−sinγcosγ0001
任意旋转均可拆为 R=Rz(α)Ry(β)Rx(γ)。这个顺序可以变,但一般默认是这个顺序。
问题:
-
对于一个旋转矩阵,其欧拉角可能不唯一。
Rz(45°)Ry(90°)Rx(45°)=Rz(90°)Ry(90°)Rx(90°)=00−1010100
-
Gimbal Lock:如果三次旋转中第二次旋转 β 的角度为 π/2,那么剩下 2 个自由度会变成 1 个。
Rz(α)=cosαsinα0−sinαcosα0001Ry(β)=cosβ0−sinβ010sinβ0cosβ=00−1010100Rx(γ)=1000cosγsinγ0−sinγcosγ
带入、合并计算:
Ry(π/2)Rx(γ)=00−10101001000cosγsinγ0−sinγcosγ=00−1sinγcosγ0cosγ−sinγ0
R=Rz(α)[Ry(π/2)Rx(γ)]=cosαsinα0−sinαcosα000100−1sinγcosγ0cosγ−sinγ0=00−1cosαsinγ−sinαcosγsinαsinγ+cosαcosγ0cosαcosγ+sinαsinγsinαcosγ−cosαsinγ0=00−1−sin(α−γ)cos(α−γ)0cos(α−γ)sin(α−γ)0
轴角表示法#
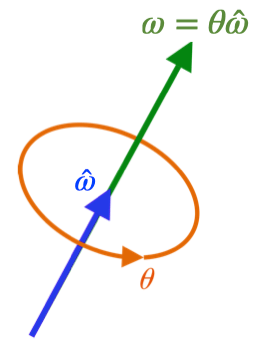
欧拉定理:任意三维空间中的旋转都可以表示为绕一个固定轴 ω^∈R3(单位向量,满足 ∥ω^∥=1)旋转一个正角度 θ 的结果。
其中:
- ω^:旋转轴的单位向量。
- θ:旋转角度(正方向遵循右手定则)。
- R∈SO(3):=Rot(ω^,θ):三维旋转矩阵,必然可以表示为绕 ω^ 旋转角度 θ 的变换。
轴角表示法的问题:
- 不唯一性:(ω^,θ) 和 (−ω^,−θ) 代表同一个旋转
- 当旋转是单位矩阵 R=I 时(即没有旋转),θ=0,此时旋转轴 ω^ 可以是任意方向。
- 当旋转角度 θ=π 时,绕轴 ω^ 和绕轴 −ω^ 旋转 π 得到的结果是相同的。这种情况对应 tr(R)=−1。
如果我们将旋转角 θ 限制在 (0,π) 这个开区间内,那么对于大部分旋转,其轴角表示就是唯一的(不考虑不旋转、旋转 π)。
轴角表示到旋转矩阵#
对于一个单位轴向量(axis)u=[x,y,z]⊤,其对应的叉乘矩阵(cross product matrix)K 定义为:
K=0z−y−z0xy−x0
其具有性质:当 K 与任意向量 v 相乘时,运算结果等同于 u 和 v 的叉乘:
Kv=0z−y−z0xy−x0v1v2v3=−zv2+yv3zv1−xv3−xv2+yv1=u×v
那么,绕单位轴 u 旋转 θ 的旋转矩阵 Rθ 可以表示为:
Rθ=cosθ⋅I+(1−cosθ)(uu⊤)+sinθ⋅K=I+(1−cosθ)(uu⊤−I)+sinθ⋅K=I+(1−cosθ)K2+sinθ⋅K
这就是 Rodrigues 旋转公式(矩阵形式)。
为了证明它,我们先证明向量形式:
Rodrigues 旋转公式(向量形式):在 3D 空间中,任意一个向量 v 沿着单位向量 u 旋转 θ 角度之后的向量 v′ 为:
v′=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)
其详细证明参见 Krasjet / Quaternion ↗ 第 2 节・三维空间中的旋转(第 11 页)。
从向量形式稍加变形,我们就能得到矩阵形式:
v′=cos(θ)v+(1−cos(θ))(u⋅v)u+sin(θ)(u×v)=cos(θ)v+(1−cos(θ))(u⊤v)u+sin(θ)(u×v)=cos(θ)v+(1−cos(θ))u(u⊤v)+sin(θ)(u×v)=[cos(θ)I+(1−cos(θ))(uu⊤)+sin(θ)K]v=Rθv
旋转矩阵 Rθ 也可以写成:
Rθ=eθK
我们可以证明后者和前者是等价的:
eθK=I+θK+2!(θK)2+3!(θK)3+⋯
而我们又有:
K2=−z2−y2xyxzxy−x2−z2yzxzyz−x2−y2
利用 u 是单位向量的性质(x2+y2+z2=1),可简化为:
K2=uu⊤−I
所以:
K3=K⋅K2=K(uu⊤−I)=Kuu⊤−K=−K
这里利用了叉乘性质 Ku=u×u=0。
所以:
K3=−K,K4=−K2,K5=K,…
带回展开形式,合并同类项:
eθK=I+(θ−3!θ3+5!θ5−⋯)K+(2!θ2−4!θ4+⋯)K2=I+sinθK+(1−cosθ)K2=I+sinθK+(1−cosθ)(uu⊤−I)=cosθI+(1−cosθ)uu⊤+sinθK=Rθ
从旋转矩阵 R 反求 (ω^,θ)#
当 θ∈(0,π) 时,可以通过以下公式从旋转矩阵 R 计算出 θ 和 ω^:
-
θ=arccos21[tr(R)−1]
-
[ω^]=2sinθ1(R−R⊤)
注意:[ω^] 表示与向量 ω^ 相关联的反对称矩阵(skew-symmetric matrix)/ 叉乘矩阵
证明:θ=arccos21[tr(R)−1]
对罗德里格公式两边取迹 (trace):
tr(R)=tr(I+sinθ[ω^]+(1−cosθ)[ω^]2)
利用迹的线性性质 tr(A+B)=tr(A)+tr(B) 和 tr(cA)=c⋅tr(A):
tr(R)=tr(I)+sinθ⋅tr([ω^])+(1−cosθ)⋅tr([ω^]2)
代入已知的迹的值:tr(I)=3, tr([ω^])=0, tr([ω^]2)=−2。
tr(R)=3+sinθ⋅0+(1−cosθ)⋅(−2)=3−2(1−cosθ)=3−2+2cosθ=1+2cosθ
整理得到 cosθ:
2cosθ=tr(R)−1cosθ=21[tr(R)−1]θ=arccos(21[tr(R)−1])
证明:[ω^]=2sinθ1(R−R⊤)
首先计算 R 的转置 R⊤。
利用性质:
-
[ω^]⊤=−[ω^]
-
([ω^]2)⊤=([ω^][ω^])⊤=[ω^]⊤[ω^]⊤=(−[ω^])(−[ω^])=[ω^]2
即 [ω^]2 是对称矩阵。
R⊤=(I+sinθ[ω^]+(1−cosθ)[ω^]2)⊤=I⊤+(sinθ[ω^])⊤+((1−cosθ)[ω^]2)⊤=I+sinθ[ω^]⊤+(1−cosθ)[ω^]2=I−sinθ[ω^]+(1−cosθ)[ω^]2
现在计算 R−R⊤:
R−R⊤=(I+sinθ[ω^]+(1−cosθ)[ω^]2)−(I−sinθ[ω^]+(1−cosθ)[ω^]2)=(I−I)+(sinθ−(−sinθ))[ω^]+((1−cosθ)−(1−cosθ))[ω^]2=0+(2sinθ)[ω^]+0=2sinθ[ω^]
当 θ∈(0,π) 时,sinθ=0,所以我们可以两边同除以 2sinθ:
[ω^]=2sinθ1(R−R⊤)
由此,我们可以定义两个旋转矩阵之间的 旋转距离。
旋转距离:从姿态 R1 转到姿态 R2 所需的最小旋转角度。
易知,两个旋转的关系是:
(R2R1⊤)R1=R2
那么,旋转距离 dist(R1,R2) 由以下公式给出(注意 θ(⋅) 是上述欧拉定理中的函数):
dist(R1,R2)=θ(R2R1⊤)=arccos(21[tr(R2R1⊤)−1])
四元数(Quaternion)#
扩展内容,下节课详细推导。
参考:
- Krasjet / Quaternion ↗
- Wiki / Quaternion ↗