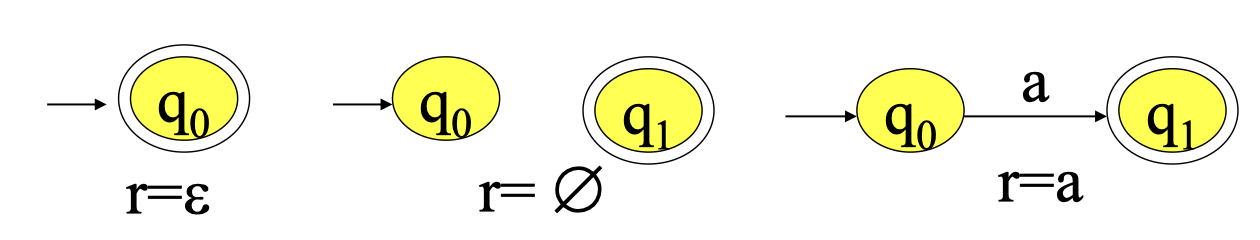从 NFA 构造 DFA#
闭包 ε_closure(S)#
定义:从状态集合 S 中 任一状态出发,仅沿 ε 弧到达的状态集合(包括 S 自身)称为 S 的 ε 闭包,记为 ε_closure(S):
T=S∪(⋃edge(t,ε)),t∈T
其中,edge(t,a) 是 M 中从状态 t 出发,仅沿 a 弧到达的状态集合。
DFA M’ 中的状态#
- M′ 中的每个状态是 M 的状态集合。
- 令 t0 是 M 的初始状态,M′ 的初始状态 d0=ε_closure({t0})。
- 包含 M 的任意终止状态的状态集合都是 M′ 中的终止状态。
DFA M’ 的转移函数#
DFAedge(d,a)=ε_closure(t∈d⋃edge(t,a))
其中:
- d 是 M 的状态集合
- a∈Σ
- edge(t,a) 是 NFA M 中从状态 t 出发,仅沿 a 弧到达的状态集合。
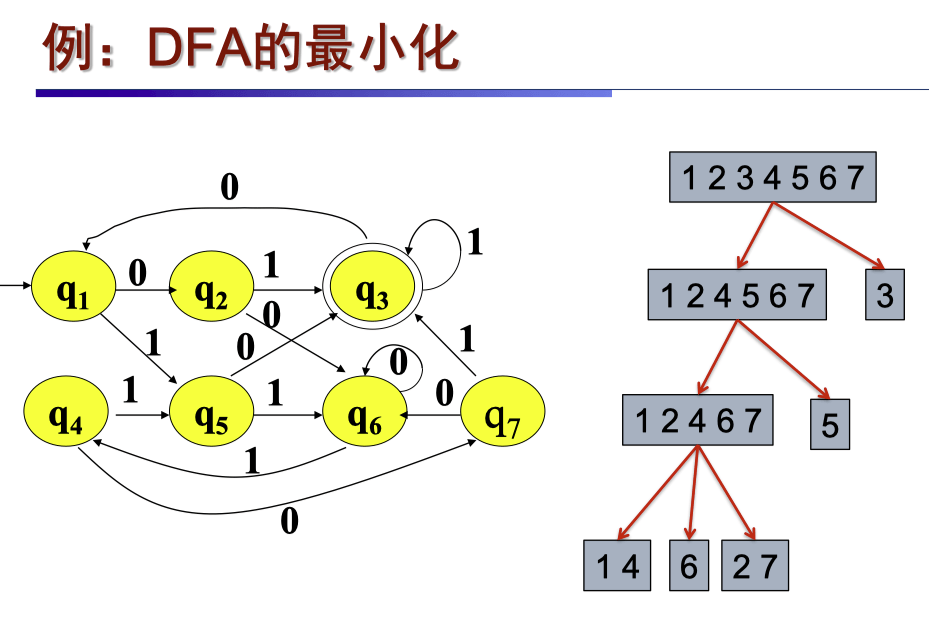
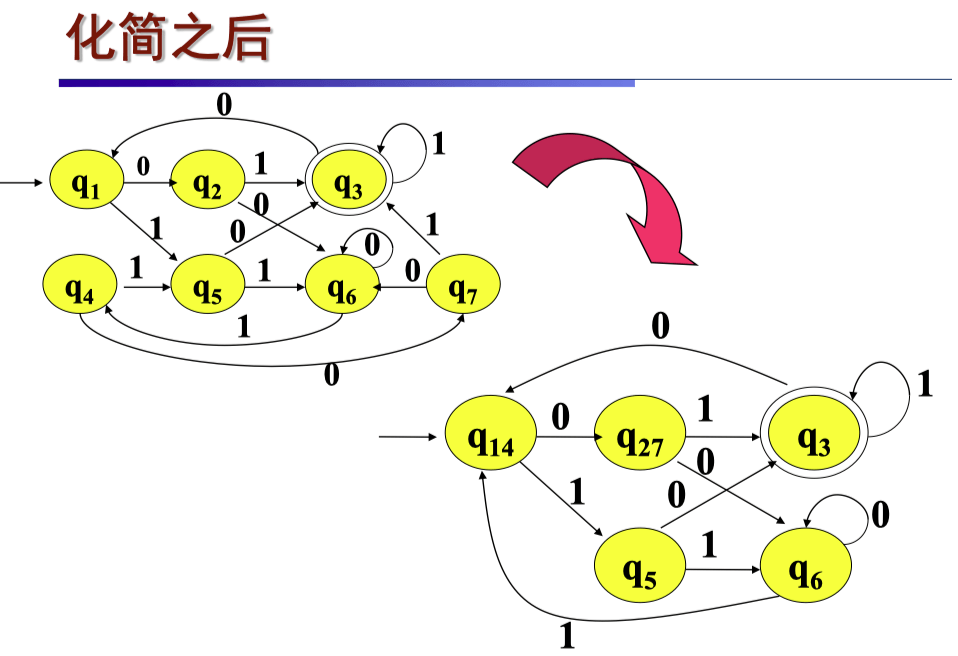
DFA 的最小化#
给定 DFA M=(Σ,Q,q0,F,δ),寻找一个状态数更少的 DFA M′,使 L(M′)=L(M)。
可以证明,存在一个最少状态的 DFA M′,使 L(M)=L(M′)。
等价状态#
- 设 p,q∈Q,若对任意 w∈Σ∗,δ(p,w)∈F 当且仅当 δ(q,w)∈F(F 是终态集合),则称 p 和 q 是等价状态
- 否则,称 p 和 q 是可区别的
等价状态的意义:如果两个状态是等价的,则可以将它们合并成一个状态而不影响 DFA 接受的语言。
等价状态的判别条件#
等价状态定义了状态集合上的等价关系。因此状态集合能被划分成等价类。
两个状态 p 和 q 等价应满足如下条件:
- 一致性条件:p 和 q 必须同时为接受状态或为非接受状态。
- 蔓延性条件:
- 对于 ∀a∈Σ,δ(p,a)=r,δ(q,a)=s,r 和 s 必须 等价
- 反之若 r 和 s 不等价,则 p 和 q 不等价
等价类划分方法#
- 把所有状态划分为两个组:接受状态组和非接受状态组。
- 任意选定一个输入符号 a,判断每个组中的各个状态对于 a 的转换,如果落入不同的组中,就把该组中的状态按照转换之后的组进行分割,使分割之后的每个组对于 a 的转换都落入同一个组。
- 重复第 2 步,直至每个组中的所有状态都等价。
感觉是一个不断二分的过程?
从正则表达式构造 FA(有限自动机)#
定理:设 r 是 Σ 上一个正则表达式,则存在 FA M 接受 L(r),并且 M 的终态是唯一的且无有向边射出。
证明:对正则表达式 r 的 运算符数目 作归纳。
设 r 具有零个运算符,必有 r=ε 或 r=∅ 或 r=a∈Σ,则 FA 分别为:
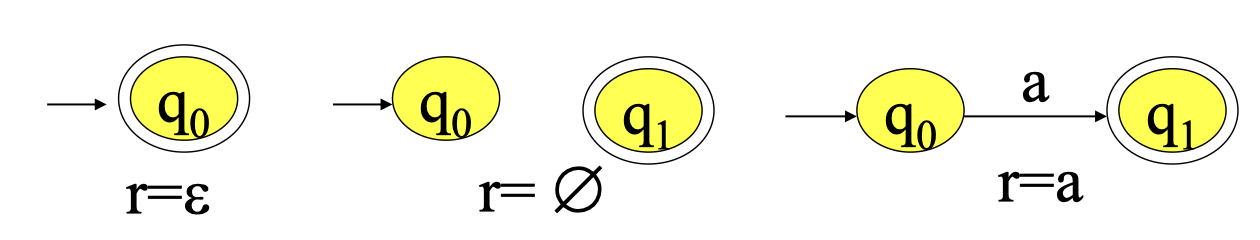
设结论对少于 i(i≤1)个运算的正则表达式 r 成立。
当 r 有 i 个运算时,有三种情况:
- r=r1∣r2
- r=r1r2
- r=r1∗
有 M1=(Σ1,Q1,q1,F1,δ1),M2=(Σ2,Q2,q2,F2,δ2) 且 L(M1)=L(r1),L(M2)=L(r2)。
由 M1 和 M2 构造 M,使得 L(M)=L(r),构造方法如图示如下:
-
情况 1:r=r1∣r2
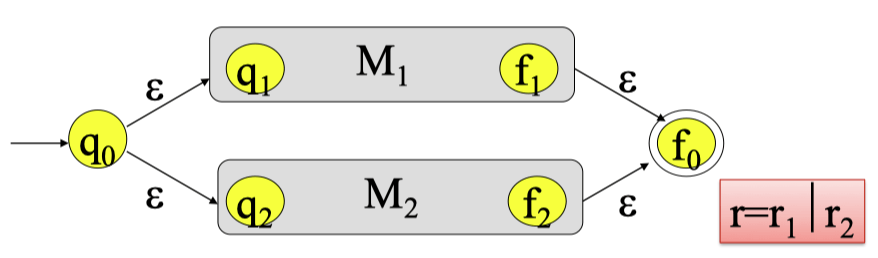
-
情况 2:r=r1r2
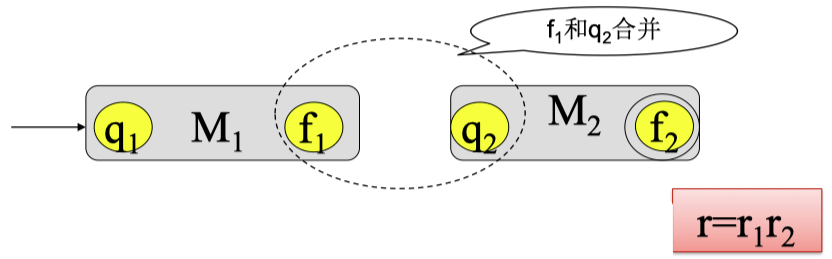
-
情况 3:r=r1∗
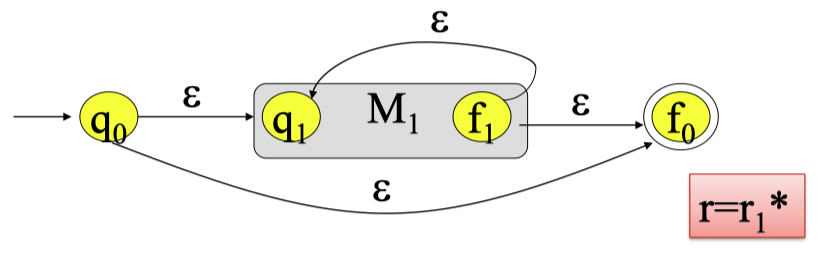
由此可以证明:假定知道 r 的计算顺序,对于任意正则表达式 r,可以构造一个 FA M,使得 L(M)=L(r)。
转换得到的 NFA 的特性#
- 状态数量最多为 r 中的运算符和运算符分量总数的两倍
- 有且只有一个开始状态和一个接受状态
- 除接受状态之外,每个状态要么有一条标号不为 ε 的出边,要么有两条标号为 ε 的出边
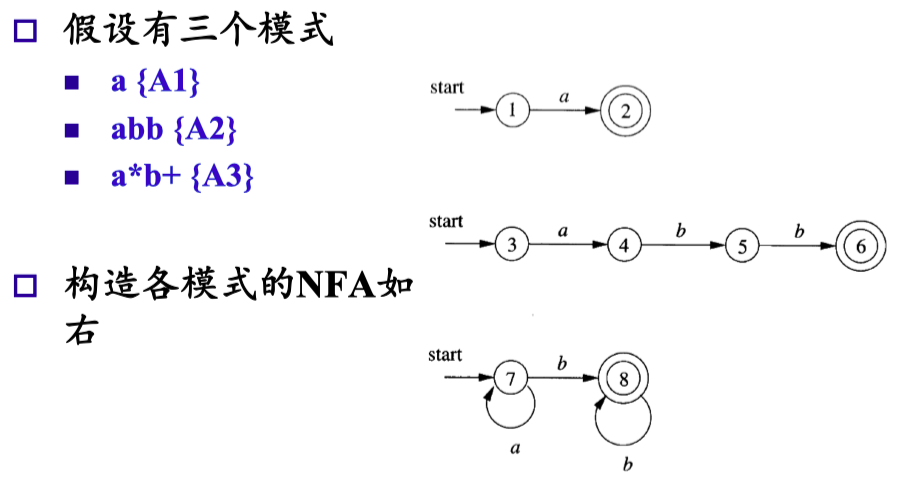
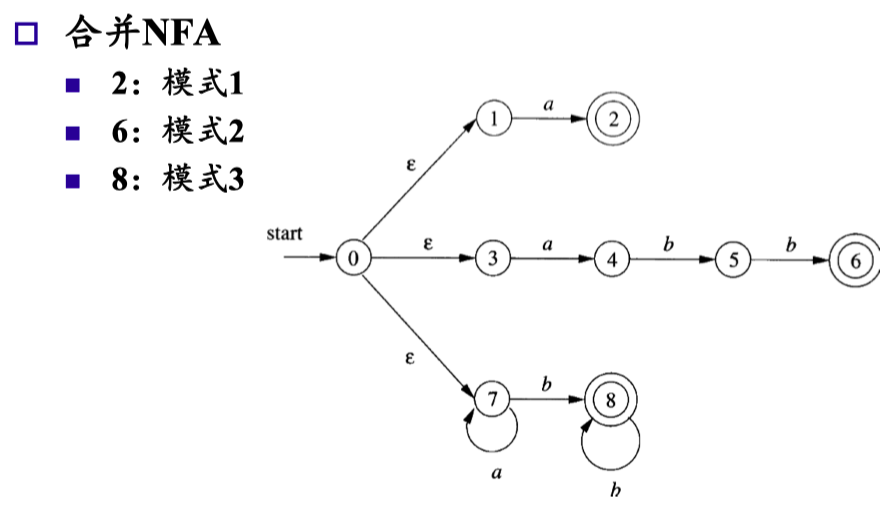
NFA 合并的方法#
- 引入新状态:引入新的开始状态 s0,并引入从这个开始状态到各个原开始状态的 ε 转换
- 语言并集:得到的 NFA 所接受的语言是原来各个 NFA 语言的 并集
- 不同接受状态:不同的接受状态可代表不同的模式
- 模式识别:不仅判断输入前缀是否 NFA 的语言,还需知道对应于哪个模式
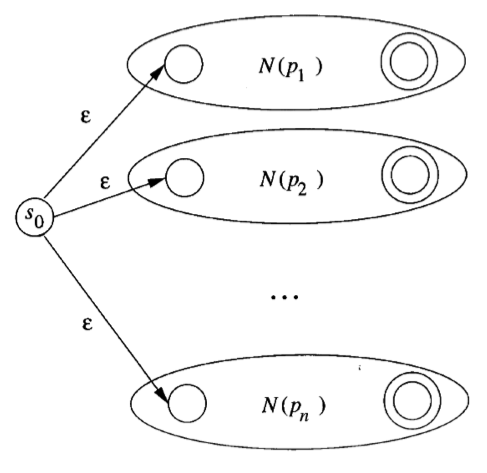
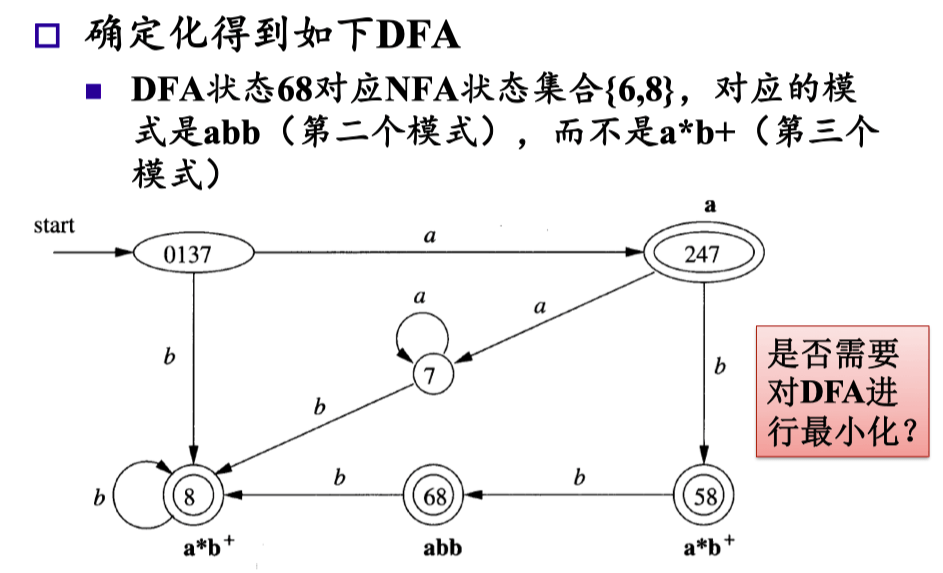
NFA 到 DFA 的转换#
-
确定化:对得到的 NFA 进行确定化,得到 DFA。
可进一步对得到的 DFA 的状态进行最小化。
-
状态集合:一个 DFA 的接受状态对应于 NFA 状态的集合,其中 至少包括一个 NFA 接受状态。
如果其中包括多个对应于不同模式的 NFA 接受状态,则表示当前的输入前缀对应于多个模式,存在冲突。
-
模式输出:找出第一个这样的模式,将这个模式作为这个 DFA 接受状态的输出。
运行的方式#
- 模拟 DFA,不断读入字符串中的字符,直到某一时刻没有后继为止(不是达到某个接受状态)
- 回头查找最后的接受状态,执行相应的动作
- 如果查不到,报告词法错误
- 在回退时,需要同时回退读入的字符