词法分析 I

词法分析器#

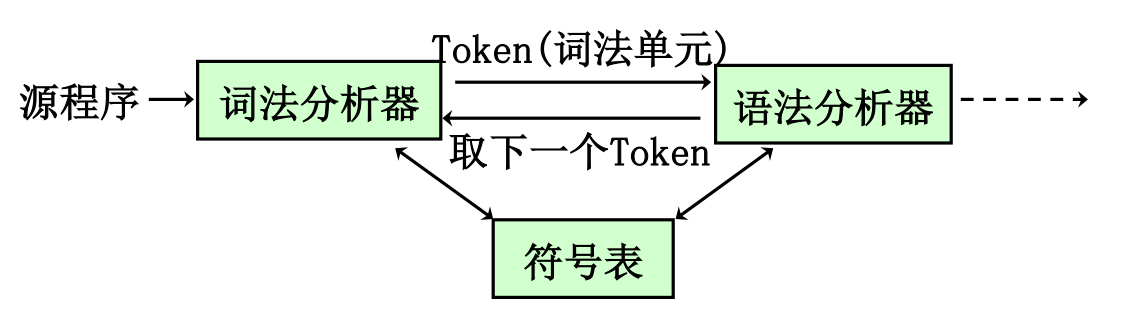
• 读入源程序字符流，输出 token 序列
• 过滤空白 / 换行 / 制表符 / 注释
• 将 token 信息添加到符号表
• 逻辑上独立于语法分析，但是通常和语法分析器在同一 Pass

基础概念#

词法单元 token#

结构：<词法单元名, 属性值(可选)>

• 单元名：表明该词法单位的种类，是表示词法单位种类的抽象符号，词法分析器通过各 token 的单元名即可确定词法单元序列的结构
• 属性值：可选，用于语义分析之后的阶段

模式 pattern#

描述一类词法单元的词素可能具有的形式

词素 lexeme#

• 源程序中的字符序列
• 如果一个词素和某个 token 的模式相匹配，它会被词法分析器识别为该 token 的实例

词法分析器的功能#

• 识别词法单元 token
• 去除注释 / 空白 / 空行 / 制表符
• 将编译器生成的错误信息关联到源文件
• 可能要进行一些 预处理：识别宏 macro；宏的扩展

token 的类别#

• 关键字 Keyword：if, else, while, return，没有属性值
• 标识符 Identifier：变量名等
• 字面常数 Literal：12，true，1e+3
• 运算符 Operator：+ - * /
• 分界符 Delimiter：逗号 / 分号 / 冒号 /etc

词法分析器的输出#

Token 的基本输出格式：<类别编码, 词法单元自身的属性值>

在词法分析过程中，有时候需要无限长的向前看

词法分析的设计#

• 可以实现为单独的一个扫描（pass）
• 也可以作为语法分析 / 语义分析的子程序，即每调用一次 getToken() 函数即获得一个 token

语言和正则表达式#

规约（Specification）：用正则表达式来描述处理词法单元时用到的模式类型

字母表 Alphabet#

字母表：符号的非空有穷集合

每一程序语言都有自己的字母表

• 机器语言：符号 0 和 1
• ASCII 字符集

符号串 String / 字 word#

已知字母表 $\Sigma$

1. $ε$ 是 $\Sigma$ 上的一个 符号串 （空串）
2. 若 $\alpha$ 是 $\Sigma$ 上的符号串，而 $a$ 是 $\Sigma$ 的元素，则 $\alpha a$ 是 $\Sigma$ 上的符号串。
3. $\beta$ 是 $\Sigma$ 上的符号串，当且仅当它由 1 和 / 或 2 导出（递归定义）。

定义：由字母表中的符号所组成的 任意有穷序列 被称为该字母表上的 符号串（String），也称作 字（Word） 。

通常约定#

• 靠前的小写字母表示 符号：$a, b, c$
• 小写希腊字母或靠后的小写英文字母表示 符号串：$α, β, γ, x ,y ,z$
• $ε$ 通常表示 空串
• 大写字母表示 符号串集合：$A,B,C$

相关概念#

设 $x$ 是一个符号串，定义如下概念：

• 前缀（prefix）：移走 $x$ 尾部的 零个 或多个连续的符号。
• 后缀（suffix）：移走 $x$ 头部的 零个 或多个连续的符号。
• 子串（substring）：从 $x$ 中删去一个前缀和一个后缀。
• 真前缀 / 真后缀 / 真子串：首先要非空（和集图不同），而且不等，即 $y\neq x\mathrm{~}\&\mathrm{~}y\neq\mathbf{\varepsilon}$
• 子序列（subsequence）：从 $x$ 中删去 零个或多个 符号（这些符号 不要求是连续的 ）。
• 逆转（reverse） ：或称转置，用 $x^R$ 表示。将 $x$ 中的符号按相反次序写出而得到的符号串。
• 长度（length） ：符号串中的符号的数目。如 $|aab| = 3$，$|\varepsilon| = 0$

符号串的运算#

1. 连接 (concatenation)

   设 $x$ 和 $y$ 是符号串，它们的连接 $xy$ 是把 $y$ 的符号写在 $x$ 的符号之后得到的符号串。

   例如，$x = ba,{~}y = nana\Rightarrow{~}xy = banana$

2. 方幂 (exponentiation)

   • $x^0 = \varepsilon$
   • $x^1 = x$
   • $x^2 = xx$
   • $x^n = x^{n-1}x$

语言（符号串集合）#

语言（language）：某个给定字母表上的一个任意的可数的符号串集合。

语言的例子#

• 空集 $\varnothing$
• 只包含空串的集合 $\{\varepsilon\}$
• 所有符合规范的 C 语言标识符的集合
• 所有语法正确的 C 语言程序的集合
• 所有语法正确的英语句子的集合

语言的运算#

设 $L$ 和 $M$ 是两个符号串集合，则：

1. 合并 (union)

   $$L \cup M = \{s | s \in L \text{ 或 } s \in M\}$$

2. 连接 (concatenation)

   $$LM = \{st | s \in L \text{ 且 } t \in M\}$$

3. 方幂 (exponentiation)

   • $L^0 = \{\varepsilon\}$
   • $L^1 = L$
   • $L^2 = LL$
   • $L^n = L^{n-1}L$

4. 语言 $L$ 的 Kleene 闭包（closure）

   记作 $L^*$：

   $$L^* = \bigcup_{i \geq 0} L^i = L^0 \cup L^1 \cup L^2 \cup L^3 \cup \ldots$$

5. 语言 $L$ 的正闭包（positive closure）

   记作 $L^+$：

   $$L^+ = L \cdot L^*$$ $$L^+ = \bigcup_{i \geq 1} L^i = L^1 \cup L^2 \cup L^3 \cup L^4 \cup \ldots$$

辨析#

1. 空集 $\varnothing$：空集是一个不包含任何元素的集合。
2. 只包含空串的集合 $\{\varepsilon\}$：这个集合包含一个元素，即空串 $\varepsilon$。空串是长度为零的字符串。

运算性质：

• 空集 $\varnothing$：没有元素。

  因此，对于任何集合 $M$，有：

  $$\varnothing M = M \varnothing = \varnothing$$

  因为空集与任何集合的笛卡尔积仍然是空集

• 集合 $\{\varepsilon\}$：只包含空串。

  这个集合包含一个元素 $\varepsilon$。对于任何集合 $M$，有：

  $$\{\varepsilon\} M = M \{\varepsilon\} = M$$

  因为空串与任何字符串的连接操作不会改变字符串

正则表达式与正则语言 Regular Expression#

定义：某个字母表 $\Sigma$ 上的正则表达式及其对应的正则集合（正则语言），满足以下条件：

1. $\varepsilon$ 是一个正则表达式，表示的语言 $L(\varepsilon) = \{\varepsilon\}$。
2. 若 $a \in \Sigma$，$a$ 是一个正则表达式，$L(a) = \{a\}$。
3. 归纳步骤：设 $r$ 和 $s$ 是 $\Sigma$ 上的正则表达式：
   • $(r) | (s)$ 是一个正则表达式，表示语言 $L(r) \cup L(s)$，即或
   • $(r)(s)$ 是一个正则表达式，表示语言 $L(r) L(s)$，即连接在一起
   • $(r)^*$ 是一个正则表达式，表示语言 $(L(r))^*$，即重复
   • $(r)$ 是一个正则表达式，表示语言 $L(r)$

注意：去掉一个正则表达式中的冗余括号之后，它表示的正则语言不变（注意运算的优先级）。

正则表达式示例#

例：$\Sigma = \{a, b\}$

• $a | b$：$\{a, b\}$
• $(a | b)(a | b)$：$\{aa, ab, ba, bb\}$
• $a^*$：$\{\varepsilon, a, aa, aaa, aaaa, \dots\}$
• $(a | b)^*$ 或 $(a^*b^*)^*$：$\{\varepsilon, a, b, aa, ab, ba, bb, aaa, \dots\}$
• $a^*b$：$\{b, ab, aab, aaab, \dots\}$

C 语言标识符：可视化 ↗

(A|B|...|Z|a|b|...|z|_)((A|B|...|Z|a|b|...|z|_ |0|1|...|9))*
// [A-Z_][A-Za-z0-9_]*

有符号整数：可视化 ↗

(+|-|ε)(0|1|...|9)(0|1|...|9)*
// [+-]?[0-9][0-9]*

正则表达式的性质#

设 $e_1, e_2, e_3$ 均为某字母表上的正则表达式，则有：

• 单位正则表达式 $\varepsilon$：$\varepsilon e = e \varepsilon = e$
• 交换律：$e_1 | e_2 = e_2 | e_1$
• 结合律：$e_1 | (e_2 | e_3) = (e_1 | e_2) | e_3$，$e_1(e_2 e_3) = (e_1 e_2)e_3$
• 分配律：$e_1(e_2 | e_3) = e_1 e_2 | e_1 e_3$，$(e_1 | e_2)e_3 = e_1 e_3 | e_2 e_3$

此外：

• $r^* = (r\varepsilon)^*$
• $r^{**} = r^*$
• $(r|s)^* = (r^* s^*)^*$

正则定义（Regular Definition）#

正则定义是如下形式的定义序列：

其中：

• $R_1, R_2, \ldots, R_n$ 为正则表达式。
• $D_1, D_2, \ldots, D_n$ 为正则表达式名字。

限定：在 $R_i$ 中只能出现字母表 $\Sigma$ 中的字符，以及前面已定义的正则表达式名字，即 $D_1, D_2, \ldots, D_{i-1}$。

我们用这种辅助定义式（相当于规则）来定义程序语言的单词符号。

正则表达式的扩展形式#

为了表达的方便，通常可以对正则表达式做如下的扩展：

• 1 次或多次出现：$(r)+$ 用来表示 $L(r)+$

  $r^* = r+|\varepsilon \quad r+ = rr^* = r^* r$

• 0 次或 1 次出现：$r?$ 用来表示 $r | \varepsilon$

  也就是 $L(r) \cup \{\varepsilon\}$

• 字符类：$[abc]$ 表示 $a|b|c$；$[a-z]$ 表示 $a|b|c|\ldots|z$

建议看 RegexLearn ↗。

例题#

写出语言 “所有相邻数字都不相同的非空数字串” 的正则定义。

解答：正则定义如下

将这些正则定义逆序排列就是答案。

1. 顶层规则 answer ：

   • answer 可以是以 0 开头的数字串，或者以 no_0 开头的数字串。
   • 对于以 0 开头的串，后面可以跟任意多个 (no_0 0)，最后再跟一个 no_0 或者为空（$\varepsilon$）。
   • 对于以 no_0 开头的串，直接匹配 no_0。

2. 子表达式 no_0 ：

   • no_0 代表不能以 0 开头的数字串，其定义类似于 answer，但替换了数字。
   • no_0 可以是以 1 开头，后面可以跟任意多个 (no_0-1 1)，最后再跟一个 no_0-1 或者为空（$\varepsilon$）。
   • 对于以 no_0-1 开头的串，直接匹配 no_0-1。

3. 递归定义 ：

   • 其他子表达式 no_0-1，no_0-2，直到 no_0-8，都以类似的方式定义，保证生成的串中相邻数字始终不同。
   • 最终，no_0-8 只能匹配 9。