CAUTION
致各位同学:本笔记的撰写目的是用作参考,请勿直接抄袭,否则后果自负。
我的推荐做法是,你可以阅读我的博文后了解都有哪些坑,但自己实现的时候千万不要看我的代码,避免抄袭风险。
PartA#
需要编写一个 csim.c 程序,来模拟缓存机制。
测试指令#
make && ./test-csim出现 TEST_CSIM_RESULTS=27 字样即代表成功。
编写细节#
感觉没什么好说的,主要是从汇编回到 C 有点陌生了,注意参数读、文件读和内存分配管理的方法就行。
具体的文件读写,系统 I/O 的知识在第十章才会讲到,这里涉及到的 FILE* 流的知识则是在 10.10 节,所以如果你现在不会的话你可以选择提前预习第十章(挺短的),或者只是先简单了解一下所需函数的使用方法。
文件读写#
#include <stdlib.h>
FILE* trace_file; // 定义文件指针
trace_file = fopen(optarg, "r"); // 打开文件
fscanf(trace_file, "%s %lx,%d\n", &operation, &address, &size) == 3; // 读取文件,返回值为成功读取的参数个数FILE *:文件指针,指向文件的指针,用于读写文件。
fopen(const char *path, const char *mode):打开文件,返回文件指针。用 r 模式打开文件,表示只读。
fscanf(FILE *stream, const char *format, ...):从文件流中读取格式化输入。
%s表示字符串%lx表示 16 进制数%d表示十进制数。返回值为成功读取的参数个数,所以这里指定为 3 个。
参数读取#
#include <getopt.h> // getopt
#include <stdlib.h> // atoi
int main(int argc, char* argv[]) {
int option;
while ((option = getopt(argc, argv, "hvs:E:b:t:")) != -1) {
switch (option) {
case 'h':
printUsage();
exit(0);
case 'v':
v = 1;
break;
case 's':
s = atoi(optarg); // 外部变量 optarg 指向当前选项参数的指针,atoi将字符串转换为整数
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
trace_file = fopen(optarg, "r");
break;
default:
printUsage();
exit(0);
}
}
}getopt(int argc, char * const argv[], const char *optstring):解析命令行参数。
argc表示参数个数argv表示参数列表optstring表示选项字符串,选项字符串中的字母表示选项,冒号表示选项后面需要参数(必填)。返回值为当前选项字母,如果没有选项了则返回 -1。
在本例中,选项字符串为
hvs:E:b:t:,表示有 5 个选项,其中s、E、b、t后面需要参数。h、v后面不需要参数。关于
optarg,可以理解为是用来保存选项的参数的,而且虽然你没有定义它,但是因为你引入了getopt.h头文件,所以它是一个外部变量,你可以直接使用它。本次测评不要求
h和v选项,所以你也可以用s:E:b:t:作为选项字符串(当然后面的逻辑也要对应修改)。
atoi(const char *nptr):将字符串转换为整数。
内存分配管理#
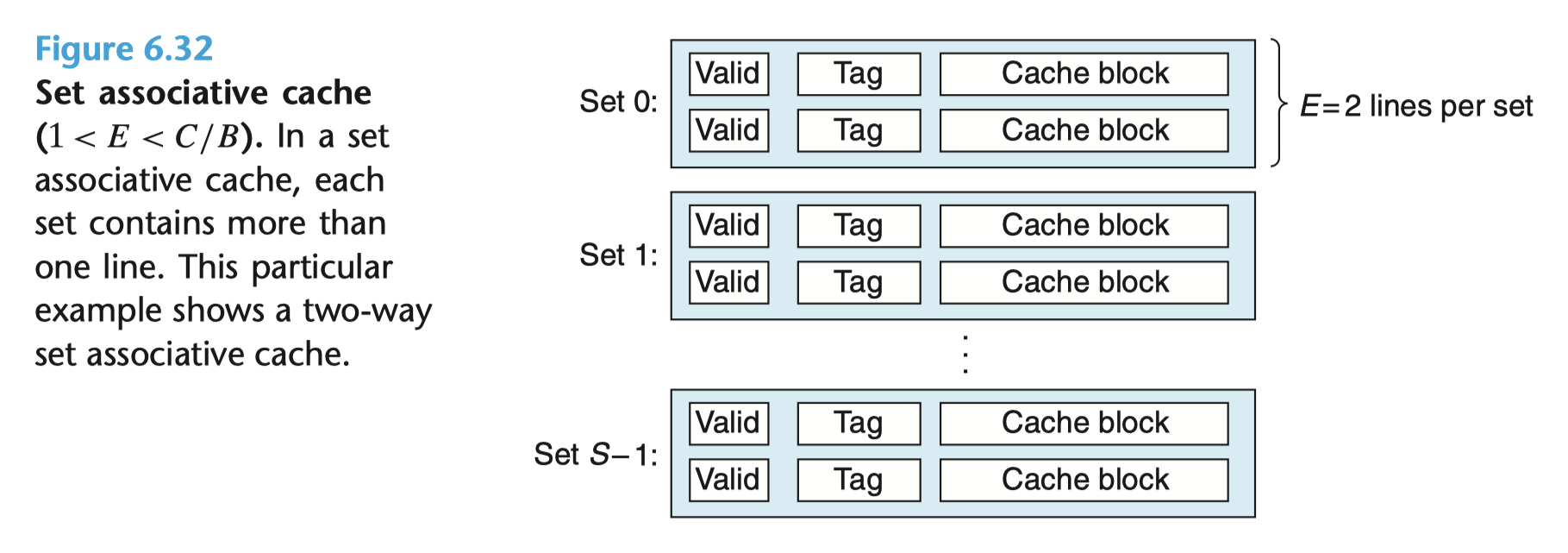
注:附图来自英文原版 CSAPP 3rd P661 Figure 6.32
struct line {
int valid; // 有效位
int tag; // 标记
int last_used_time; // 最后使用时间
}; // 字节信息是没用的,不用存
// 定义组,每个组有 E 个行
typedef struct line* set;
// 定义缓存,有 S 个组
set* cache;
// 初始化缓存
cache = (set*)malloc(sizeof(set) * (1 << s));
for (int i = 0; i < (1 << s); i++) {
cache[i] = (set)malloc(sizeof(struct line) * E);
for (int j = 0; j < E; j++) {
cache[i][j].valid = -1;
cache[i][j].tag = -1;
cache[i][j].last_used_time = -1;
}
}注意结构体使用 sizeof 时,要加上 struct 关键字。
cache 是一个 set 数组,每个 set 有 E 个 line,每个 line 有 3 个参数,分别是 valid、tag 和 last_used_time。
因而 cache 的类型是 set*,即指向 set 的指针,而 set 的类型是 line*,即指向 line 的指针。
malloc和calloc都是动态分配内存的函数,malloc只分配内存,calloc分配内存并初始化为 0。malloc的参数为分配的字节数,calloc的参数为分配的个数和每个元素的字节数。
别忘了最后释放内存:
free(cache);踩坑#
Modify 跳转技巧#
Modify 修改操作 = Load 加载操作 + Store 存储操作,所以在 M 操作时,需要访问两次缓存。
你编写的程序不用支持 -v 参数,所以你可以使用如下的跳转表:
switch (operation) {
case 'I':
continue;
case 'M': // Modify = Load + Store
useCache(address);
case 'L': // Load
case 'S': // Store
useCache(address);
}这种写法可以让 M 操作直接多执行一次 useCache 函数,而不用再写一遍。但是,如果你想追求效率(尽管这个 Part 并不要求)或者想要支持 -v 参数,那么你可以直接多给 useCache 传递一个 is_modify 参数,来判断是否为 M 操作。若是,则可以直接令第二次写为 HIT,而不用再次访问缓存。具体实现可以参考我的代码。
值得一提的是,在所有的测试样例中,只有 mem.trace 中存在 M 操作,而 handout 中给出的测试命令行均没有测试它,也就没有测试 M 操作的正确性。你必须使用 test-csim 来测试 M 操作的正确性。
地址是 64 位,而不是 32 位#
在 csim.c 中,地址是 64 位的,而不是 32 位的。所以你需要使用 %lx 来读取地址。同时你不能使用 int 类型来存储地址,而应该使用 unsigned long 或者 __uint64_t 类型或者 size_t 类型(执行的机器是 64 位的)。
另外注意对取地址时,一定要注意是否设置了对于高位(tag 位)的掩码,否则可能会出现段错误(数组越界了)。
int set_pos = address >> b & ((1 << s) - 1);LRU(Least Recently Used)算法#
初始化一个 line 的时候,也许将 last_used_time 初始化为 -1 会更好(区别于初始的 timestamp = 0)。因为这样可以判断这个 line 是否被使用过(即判断是否为冷不命中,决定是否要给 eviction 加一)。
在每次执行 useCache 的时候,让 timestamp 加一,即可维护一个时间戳(而不用使用什么标准库的时间戳,那样会导致两个问题,一个是可能精度不够(每次执行 useCache 的时间间隔可能太短),另一个是可能还要处理浮点数问题)。
同时,在遍历一个组的时候,你可以合并遍历和查找最小时间戳的操作,这样可以减少一次遍历。
其他#
printSummary() 函数定义在 cachelab.h 中,所以你需要在 csim.c 中引入 cachelab.h 头文件。
puts 和 printf 函数都可以用来输出字符串,但是 puts 函数会自动在字符串后面加上换行符,而 printf 函数不会。
#include "cachelab.h"
printSummary(hit, miss, eviction);如何理解地址的缓存#
我的理解是,对于原本标记 “在内存中的地址(一串 64 位十六进制数)”,通过拆分出 Tag/Set/Byte 这三段,映射到了缓存中的唯一地方(类似于一个哈希函数,大范围到小范围,但是保证了一定的局部性)。当然,映射时就会出现类似冲突 / 驱逐(类似哈希冲突,本质是小范围映射会损失,无法真的不冲突地放下所有的大范围地址)的问题。
成品代码#
// Arthals 2110306206@stu.pku.edu.cn
// File : csim.c
// Time : 2023-11-03 09:06:08
// Author : Arthals
// Software: Visual Studio Code
#include <stdio.h>
#include <getopt.h>
#include <stdlib.h>
#include "cachelab.h"
struct line {
int valid;
int tag;
int last_used_time;
};
// 定义组,每个组有 E 个行
typedef struct line* set;
// 定义缓存,有 S 个组
set* cache;
// 定义全局缓存参数
int v = 0, s, E, b, t, timestamp = 0;
// 定义全局返回参数
unsigned hit = 0, miss = 0, eviction = 0;
void printUsage() {
puts("Usage: ./csim [-hv] -s <num> -E <num> -b <num> -t <file>");
puts("Options:");
puts(" -h Print this help message.");
puts(" -v Optional verbose flag.");
puts(" -s <num> Number of set index bits.");
puts(" -E <num> Number of lines per set.");
puts(" -b <num> Number of block offset bits.");
puts(" -t <file> Trace file.");
puts("");
puts("Examples:");
puts(" linux> ./csim -s 4 -E 1 -b 4 -t traces/yi.trace");
puts(" linux> ./csim -v -s 8 -E 2 -b 4 -t traces/yi.trace");
}
void useCache(size_t address, int is_modify) {
int set_pos = address >> b & ((1 << s) - 1);
int tag = address >> (b + s);
set cur_set = cache[set_pos];
int lru_pos = 0, lru_time = cur_set[0].last_used_time;
for (int i = 0;i < E;++i) {
if (cur_set[i].tag == tag) {
++hit;
// 如果是修改操作,那么还有一次写,会加一次命中(已被加载)
hit += is_modify;
cur_set[i].last_used_time = timestamp;
if (v) {
printf("hit\n");
}
return;
}
if (cur_set[i].last_used_time < lru_time) {
lru_time = cur_set[i].last_used_time;
lru_pos = i;
}
}
++miss;
// 修改操作时,还有写的一次命中(已驱逐后加载)
hit += is_modify;
// 冷不命中
eviction += (lru_time != -1);
if (v) {
if (lru_time != -1) {
if (is_modify)
printf("miss eviction hit\n");
else
printf("miss eviction\n");
}
else {
printf("miss\n");
}
}
// 驱逐
cur_set[lru_pos].last_used_time = timestamp;
cur_set[lru_pos].tag = tag;
return;
}
int main(int argc, char* argv[]) {
int option;
FILE* trace_file;
// 获取参数
if (argc == 1) {
printUsage();
exit(0);
}
// 读取参数
while ((option = getopt(argc, argv, "hvs:E:b:t:")) != -1) {
switch (option) {
case 'h':
printUsage();
exit(0);
case 'v':
v = 1;
break;
case 's':
s = atoi(optarg); // 外部变量 optarg 指向当前选项参数的指针,stdlib::atoi将字符串转换为整数
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
trace_file = fopen(optarg, "r");
break;
default:
printUsage();
exit(0);
}
}
// 校验参数
if (s <= 0 || E <= 0 || b <= 0 || s + b > 64 || trace_file == NULL) {
printUsage();
exit(1);
}
// 设置校验位数,发现没用到,遂注释
// t = 64 - s - b;
// 初始化缓存
cache = (set*)malloc(sizeof(set) * (1 << s));
for (int i = 0; i < (1 << s); i++) {
cache[i] = (set)malloc(sizeof(struct line) * E);
for (int j = 0; j < E; j++) {
cache[i][j].valid = -1;
cache[i][j].tag = -1;
cache[i][j].last_used_time = -1;
}
}
// S 38c08c, 1
// L 30c080, 4
// M 30c080, 4
int size;
char operation;
size_t address;
while (fscanf(trace_file, "%s %lx,%d\n", &operation, &address, &size) == 3) {
++timestamp;
if (v) {
printf("%c %lx,%d ", operation, address, size);
}
switch (operation) {
case 'I':
continue;
case 'M': // Modify = Load + Store
useCache(address, 1);
break;
case 'L': // Load
case 'S': // Store
useCache(address, 0);
}
}
free(cache);
printSummary(hit, miss, eviction);
}
运行:
make && ./test-csim得到:
Your simulator Reference simulator
Points (s,E,b) Hits Misses Evicts Hits Misses Evicts
3 (1,1,1) 9 8 6 9 8 6 traces/yi2.trace
3 (4,2,4) 4 5 2 4 5 2 traces/yi.trace
3 (2,1,4) 2 3 1 2 3 1 traces/dave.trace
3 (2,1,3) 694 453 449 694 453 449 traces/mem.trace
3 (2,2,3) 201 37 29 201 37 29 traces/trans.trace
3 (2,4,3) 212 26 10 212 26 10 traces/trans.trace
3 (5,1,5) 231 7 0 231 7 0 traces/trans.trace
6 (5,1,5) 265189 21777 21745 265189 21777 21745 traces/long.trace
27
TEST_CSIM_RESULTS=27大功告成!
PartB#
缓存参数:s = 5, E = 1, b = 5。
所以这是一个有 32 个组()的直接映射高速缓存(),每个组只有 1 个块,每个块有 32 个字节()。
也就是说,一共可以放得下 1024 个字节,即 256 个 int。
32x32#
测试指令:
make && ./test-trans -M 32 -N 32满分线:misses <= 300。
观察到示例转置函数的结果:hits:869, misses:1184, evictions:1152
显然这是极差的,因为 A 和 B 的大小一致,而且存储的地址偏差正好使得其对应位置的数据都在同一个组(行 / 块)中(初始地址映射的块相同)。
以下讨论何时会出现冲突。考虑默认程序,我们总是需要将 A[i][j] 读出后写到 B[j][i]。
因而,我们需要考虑他们各自在上级缓存中的位置。你可以认为行优先读时,每 8 个连续的 int 总是映射到同一个 Set/Block(即 A[i][8k+0] ~ A[i][8k+7])。对 B 同理。
所以,我们发现,直接按元素写的时候,会出现大量的不命中。但是实际是不命中只有 1184 次,如果每个读写都造成两次不命中显然不止这么点,那么什么时候会命中?
考虑读 A[i][j] 时,我们总要写 B[j][i]。因而存储着两个数据的块的起始偏移量地址(按照 int 数计算)分别为:
A[i][j]:i × 32 + jB[j][i]:j × 32 + i
由于每 8 个 int 偏移一个缓存 Set,所以在缓存中,两个块分别存储如下:
A[i][j]:存储在第⌊(i × 4 + ⌊j/8⌋)/32⌋个块,存储着A[i][ ⌊j/8⌋ ]~A[i][ ⌊j/8⌋+7 ]B[j][i]:存储在第⌊(j × 4 + ⌊i/8⌋)/32⌋个块,存储着B[j][ ⌊i/8⌋ ]~B[j][ ⌊i/8⌋+7 ]
所以,当 i = j 时,两个块的 Set 会发生冲突,导致大量的不命中。而当 i != j 时,两个块的 Set 不会发生冲突。
- 对于读 A 操作来说,我们往往具有很好的局部性,因为是行优先读,所以每 8 个数,除了第一次加载,后面的 7 次都会命中。
- 对于写 B 操作来说,我们完全没有利用局部性。考虑我们写 B 的第 j 行,我们第一次写(
B[j][0])和第二次写(B[j][1])之间至少包括了对 B 的一整列(列优先,31 行,B[j+1][0]~B[j-1][1])的全部写,而我们的缓存大小只有 256 个数的大小(即 8 行),当前行早就被刷掉了,所以我们写 B 完全没机会出现命中。而且在对角线处时,我们还会因为要写 B 而导致对于已经读入的 A 的行发生冲突不命中(即要发生一次驱逐)。
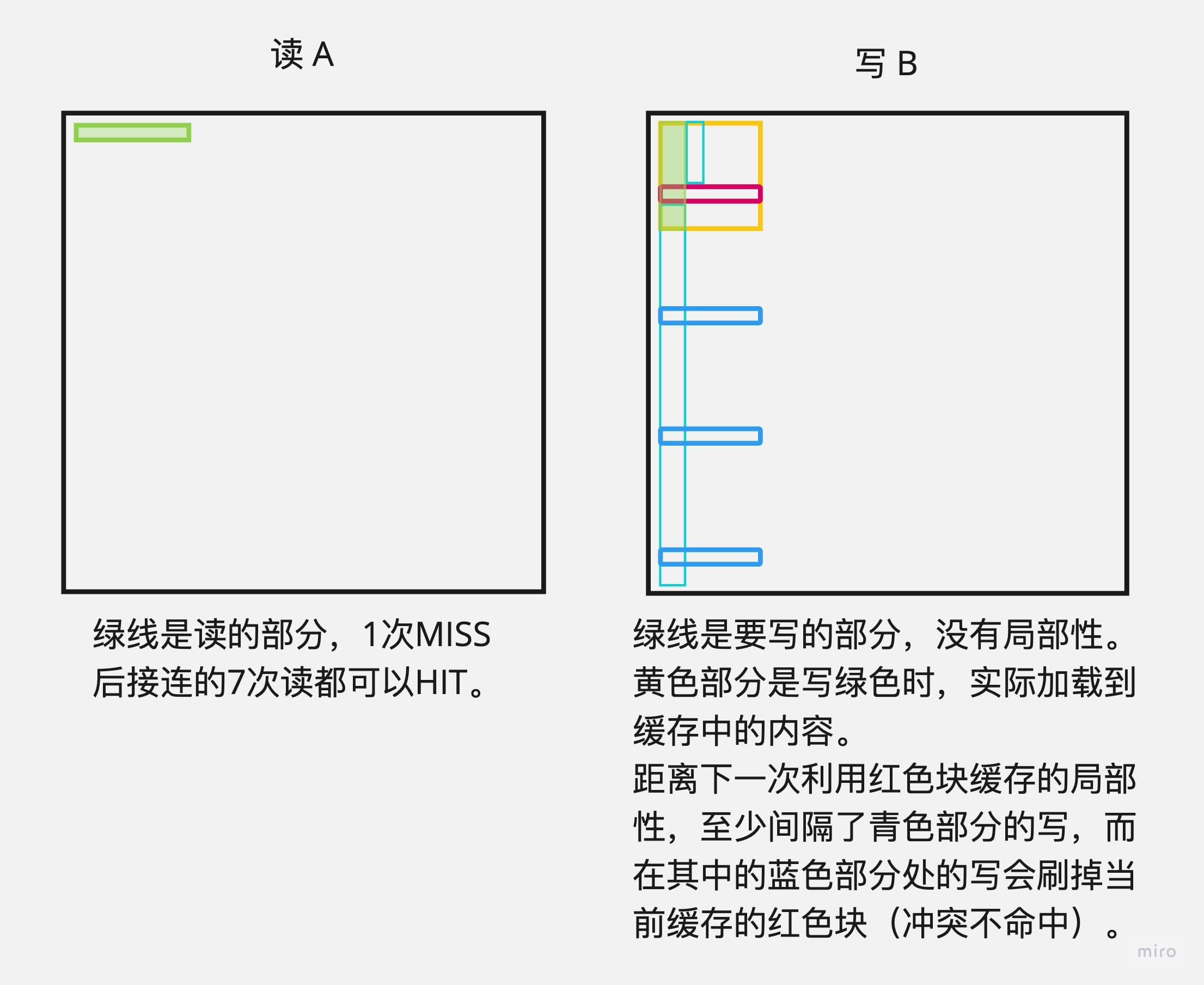
所以整体计算下来,应当发生 1024(写 B 全部不命中)+ 4(写 A 每行每 8 个数不命中一次)* 32(写 A 的行)+ 32(对角线处写 B 造成读 A 驱逐,需要重新读一次),即 1184 次不命中。
此处写这么细,是因为后续处理别的尺寸的时候也可以进行类似的推导。
调用 csim-ref 来查看 trace:
./csim-ref -v -s 5 -E 1 -b 5 -t trace.f1 > trace.f1.v果不其然,有大量的 miss:
L 10e0c0,4 miss
S 14e4a0,4 miss eviction
L 10e0c4,4 hit
S 14e520,4 miss eviction
L 10e0c8,4 hit
S 14e5a0,4 miss eviction
L 10e0cc,4 hit
S 14e620,4 miss eviction
L 10e0d0,4 hit
S 14e6a0,4 miss eviction
L 10e0d4,4 hit
S 14e720,4 miss eviction
L 10e0d8,4 hit
S 14e7a0,4 miss eviction
L 10e0dc,4 hit
S 14e820,4 miss eviction
L 10e0e0,4 miss eviction
S 14e8a0,4 miss eviction于是,我们很自然的想到,通过限制写 B 的范围,来利用 B 的局部性。而这也就是书上讲过的分块技巧:将 32x32 的矩阵分成 8x8 的小块,这样就可以充分利用局部性,读 A 一次连续读入 8 个元素,然后转置,再连续写入 B。即避免了对于写 B 时,因为列优先顺序写造成的缓存驱逐。
同时我们使用多个局部变量来存储从 A 读出来的数据,这样可以最大化地利用局部性。
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
REQUIRES(M > 0);
REQUIRES(N > 0);
// s = 5, E = 1, b = 5
// 总变量:4 个循环变量 + 8 个临时变量 = 12 个变量
int a, b, c, d, e, f, g, h;
if (M == 32) {
// 先把 A 复制 B,再转置 B,避免因为 A 的下一次读驱逐 B 的同一行,导致 B 的下一次写 MISS
// 8*8 分块
// 总 MISS:16(块数)*[8(读)+8(写)] = 256
// 显示 MISS = 260,但是通过添加 trans() 的代码并清空缓存,然后对比测试差异,可知实际只有 256 个 MISS
// 故猜测那 4 个多的 MISS 可能是别的函数调用所致,也可通过观察 trace.f0 发现确实开头多了 1 个 S 和 3 个 L
for (int i = 0; i < N; i += 8) { // 当前行
for (int j = 0; j < M; j += 8) { // 当前列
// 首先将 A[i][j]~A[i+7][j+7] 复制到 B[j][i]~B[j+7][i+7]
for (int k = 0;k < 8;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
e = A[i + k][j + 4];
f = A[i + k][j + 5];
g = A[i + k][j + 6];
h = A[i + k][j + 7];
B[j][i + k] = a;
B[j + 1][i + k] = b;
B[j + 2][i + k] = c;
B[j + 3][i + k] = d;
B[j + 4][i + k] = e;
B[j + 5][i + k] = f;
B[j + 6][i + k] = g;
B[j + 7][i + k] = h;
}
}
}
}
ENSURES(is_transpose(M, N, A, B));
}运行:
make && ./test-trans -M 32 -N 32得到:
func 0 (Transpose submission): hits:1765, misses:288, evictions:256可以发现我们已经将 miss 降低到了 288,小于 300 的满分限,收获满分!
但是,这就是完美无缺的吗?显然不是,我们可以继续优化。
注意到理论最优 MISS 数应当是 16(块数) * [8(读A)+8(写B)] = 256 次,为什么会多出来 32 次呢?
这是因为当 i=j 时,A[i][i] 和 B[i][i] 的组数是一样的,所以每次处理对角线上的块时,都会额外出现 8 次 MISS:
- 写 B 的第 i 列,导致 A 的第 i+1 行被驱逐
- 读 A 的第 i+1 行,导致 B 的第 i+1 行被驱逐
- 写 B 的第 i+1 列,冲突不命中
- …
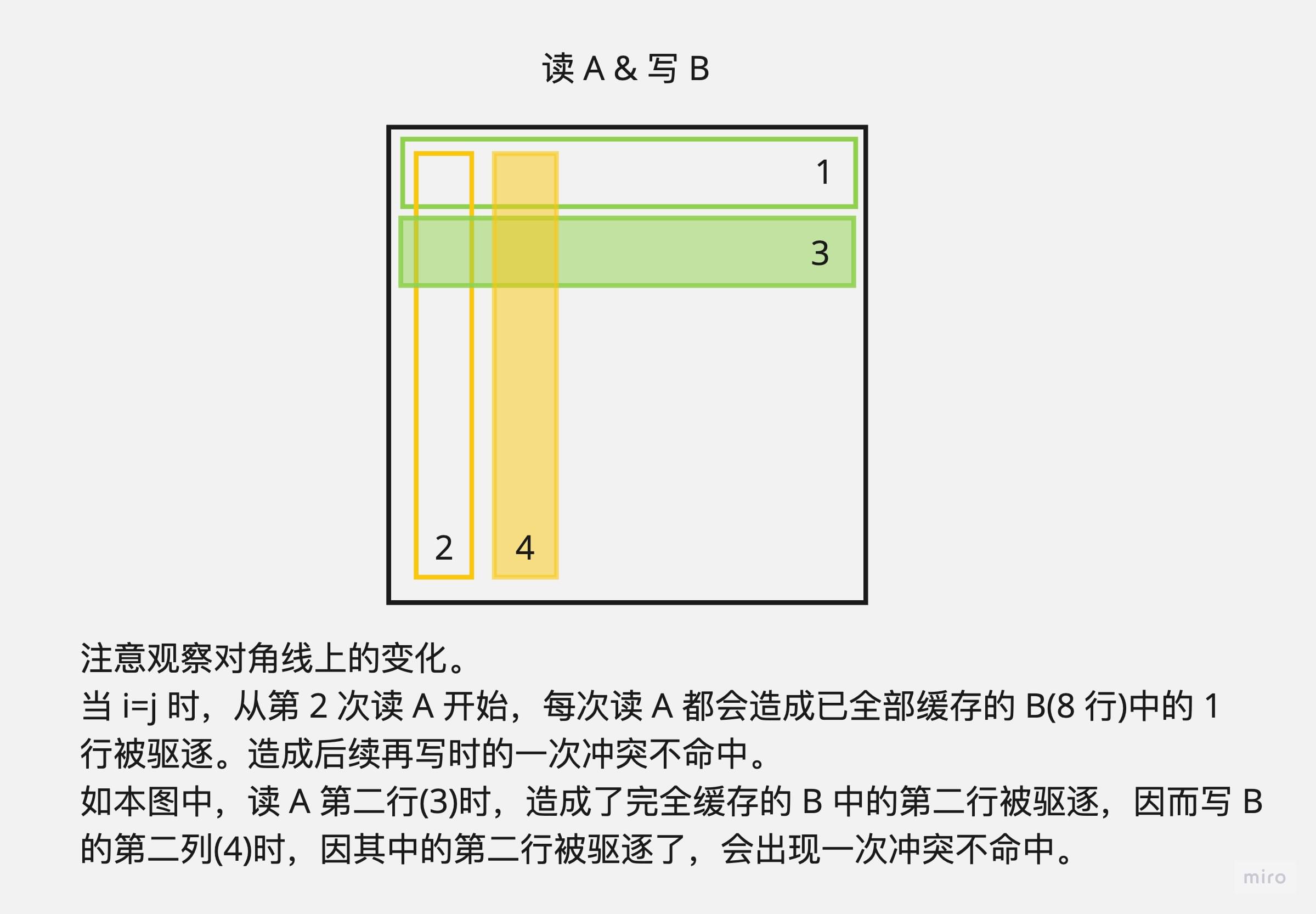
有没有什么优化方法呢?当然是有的,我们可以先将 A 的一个块完整、不转置地复制到 B,然后再转置 B,这样对 B 的转置与写时,因为 B 已经完全加载到了缓存中,所以不会出现任何的不命中。
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
REQUIRES(M > 0);
REQUIRES(N > 0);
// s = 5, E = 1, b = 5
// 总变量:4 个循环变量 + 8 个临时变量 = 12 个变量
int a, b, c, d, e, f, g, h;
if (M == 32) {
// 先把 A 复制 B,再转置 B,避免因为 A 的下一次读驱逐 B 的同一行,导致 B 的下一次写 MISS
// 8*8 分块
// 总 MISS:16(块数)*[8(读)+8(写)] = 256
// 显示 MISS = 260,但是通过添加 trans() 的代码并清空缓存,然后对比测试差异,可知实际只有 256 个 MISS
// 故猜测那 4 个多的 MISS 可能是别的函数调用所致,也可通过观察 trace.f0 发现确实开头多了 1 个 S 和 3 个 L
for (int i = 0; i < N; i += 8) { // 当前行
for (int j = 0; j < M; j += 8) { // 当前列
// 首先将 A[i][j]~A[i+7][j+7] 复制到 B[j][i]~B[j+7][i+7]
for (int k = 0;k < 8;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
e = A[i + k][j + 4];
f = A[i + k][j + 5];
g = A[i + k][j + 6];
h = A[i + k][j + 7];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
B[j + k][i + 4] = e;
B[j + k][i + 5] = f;
B[j + k][i + 6] = g;
B[j + k][i + 7] = h;
}
// 转置 B
for (int k = 0;k < 8;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
}
ENSURES(is_transpose(M, N, A, B));
}运行:
make && ./test-trans -M 32 -N 32得到:
Summary for official submission (func 0): correctness=1 misses=260可以发现我们已经将 miss 降低到了 260,非常接近理论值 256 了,而经过测试,这 4 个多出来的 MISS 其实函数调用所致。
64x64#
测试指令:
make && ./test-trans -M 64 -N 64满分线:misses <= 1300。
首先,我们直接使用 32x32 中的代码:
if (M == 32 || M==64){...}得到输出:
Summary for official submission (func 0): correctness=1 misses=3332发现 miss 过多,这是为什么呢?
回忆一下我们的 cache 参数:s = 5, E = 1, b = 5,即 block 有 32 个字节(存 8 个 int) ,32 个组,每个组只有 1 个行。所以我们的缓存总容量是 256 个 int,而 64x64 的矩阵 4 行即可占用 256 个 int,所以我们 8x8 分块后,上半块和下半块的数据会发生冲突不命中,换句话说,就是读 A[i][0] 和 A[i+4][0] 时会造成冲突不命中,写 B 同理。
如果直接修改代码改成 4x4 分块,我们的确就可以解决这个问题:
if (M == 64) {
for (int i = 0; i < N; i += 4) { // 当前行
for (int j = 0; j < M; j += 4) { // 当前列
// 首先将 A[i][j]~A[i+3][j+3] 复制到 B[j][i]~B[j+3][i+3]
for (int k = 0;k < 4;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
}
// 转置 B
for (int k = 0;k < 4;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
}运行:
make && ./test-trans -M 64 -N 64得到:
Summary for official submission (func 0): correctness=1 misses=1604收获了 4.5 分,但是仍然不够理想。
注意这里不能采用 4x8 分块,因为这样虽然可以避免 A 矩阵的读的冲突不命中,但是 B 矩阵的写的冲突不命中仍然存在。
不过这也启发了我们,既然可以通过 4x8 分块首先避免对于 A 矩阵的读的冲突不命中,那么 B 矩阵的写的冲突不命中是不是可以通过 “暂时性” 地将后 4 个元素先放到同一行的块里来避免呢?
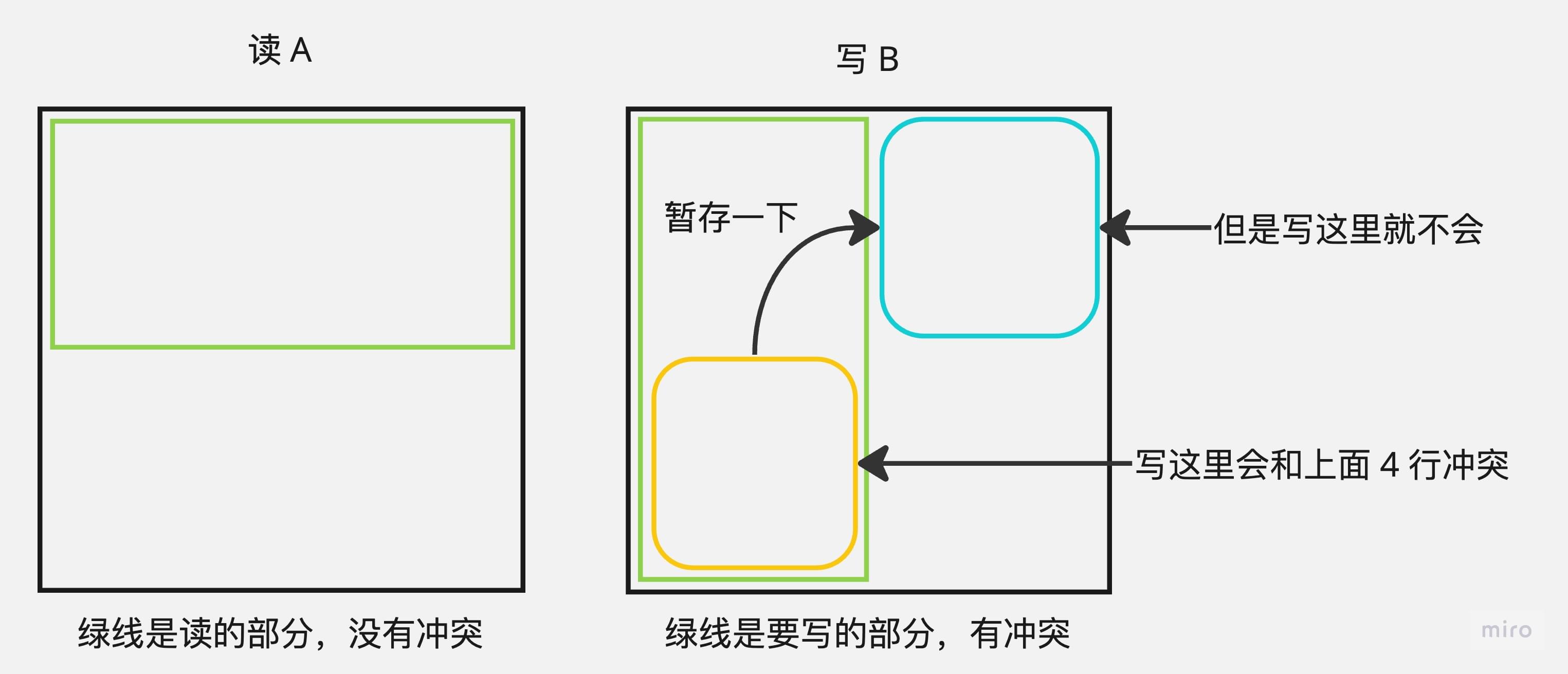
于是我们得到了优化思路:既然直接 8x8 分块不行,那我们就先 8x8 分大块,再在每个大块内 4x4 地分小块,然后注意,读完 A 的第一行(8 个 int)后,我们将前 4 个正常转置并写入 B,然后将后 4 个先放到一个暂时存储块中,这样就可以避免写下半块时的冲突不命中了。
考虑 α[2][2]、β[2][2] 为 A、B 8x8 分块之后的矩阵再进行 4x4 分块得到的子矩阵,其每个元素都是 4x4 个 int 。
以下所有代码说明,建议参照 NFLS-CHINA / CSAPP - Cache Lab 的更(最)优秀的解法 ↗ 一文的图片对照着看,我相信你会有更好的理解。
for (int i = 0; i < N; i += 8) { // 当前行
for (int j = 0; j < M; j += 8) { // 当前列
// 先复制
for (int k = 0;k < 4;++k) {
// 从 A 中取 α[0][0]+α[0][1]的第 k 行,执行 4 次,即读出 A 的上半块,每次循环,读 A 都必然 MISS
// 所以总计 4 次 MISS。
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
e = A[i + k][j + 4];
f = A[i + k][j + 5];
g = A[i + k][j + 6];
h = A[i + k][j + 7];
// 转置前四个数到 β[0][0] 的第 k 列,4 次 MISS
// 若 i=j 还会因为上一步读 A 造成冲突不命中,所以额外造成 3 次冲突不命中。
B[j][i + k] = a;
B[j + 1][i + k] = b;
B[j + 2][i + k] = c;
B[j + 3][i + k] = d;
// 将后四个转置后,先复制到 β[0][1] 的第 k 列
// 可以避免此时去写 β[1][0] 的冲突不命中
B[j][i + k + 4] = e;
B[j + 1][i + k + 4] = f;
B[j + 2][i + k + 4] = g;
B[j + 3][i + k + 4] = h;
}
}
}- 对于 i ≠ j:4 + 4 = 8 次 MISS
- 对于 i = j: 4 + 4 + 3 = 11 次 MISS
此时,已经转置完毕 β[0][0](左上矩阵),而转置好的 β[1][0](左下矩阵)暂时位于 β[0][1](右上矩阵)。
同时,A 的前四行已经完全被读完并用完了。所以我们可以放心的开始读 A 的后四行了。
// 此时,已经转置完毕 β[0][0]
// 转置好的 β[1][0] 位于 β[0][1]
// 移动 β[0][1] 到 β[1][0]
// 同时将 α[1][0] 复制并转置到 β[0][1]
for (int k = 0;k < 4;++k) {
// 读 α[1][0] 的第 k 列,首次循环造成 4 次 MISS,后续循环均 HIT
// 对于 i=j 时,因为循环间读 B (见下一步,位于上半块)会造成 1 次冲突不命中,原有的一行缓存被驱逐
// 所以总计造成 4 / 7 次 MISS
e = A[i + 4][j + k];
f = A[i + 5][j + k];
g = A[i + 6][j + k];
h = A[i + 7][j + k];
// 复制 β[0][1] 的第 k 行,一定是行优先读,否则写的时候会出现额外的冲突不命中
// 若 i ≠ j 时因为上一部分最后写了这里,所以全部命中
// 若 i=j,每次循环都会因为上一步读 A 造成了冲突不命中,所以每次循环 1 次 MISS,总计 4 次 MISS
// 所以总计造成 0 / 4 次 MISS
a = B[j + k][i + 4];
b = B[j + k][i + 5];
c = B[j + k][i + 6];
d = B[j + k][i + 7];
// 将 α[1][0] 的第 k 列复制到 β[0][1] 的第 k 行,因为上一步读的时候已经完成缓存,所以写的时候不会 MISS
B[j + k][i + 4] = e;
B[j + k][i + 5] = f;
B[j + k][i + 6] = g;
B[j + k][i + 7] = h;
// 将 β[0][1] 的第 k 行复制到 β[1][0] 的第 k 行
// 注意你这里是按行读写的,所以对于所有情况,每次循环造成 1 次冲突不命中(上一步读上半块了,一定没缓存了)
// 所以总计造成 4 次 MISS
B[j + k + 4][i] = a;
B[j + k + 4][i + 1] = b;
B[j + k + 4][i + 2] = c;
B[j + k + 4][i + 3] = d;
}这里我们已经将 β[1][0](左下矩阵)交换回正确的位置,以及转置了 β[0][1](右上矩阵)。
- 对于 i ≠ j:4 + 4 = 8 次 MISS
- 对于 i = j: 7 + 4 + 4 = 15 次 MISS
注意我们先读 A 再读 B,这里也可以先读 B 再读 A ,两者没有区别。我原以为,读 β[0][1](右上矩阵)(实际上存的是 β[1][0](左下矩阵)) 接写 β[0][1](右上矩阵)可以避免 MISS,但实际测试无影响。读者可以思考一下是为什么。
而 β[1][1](右下矩阵)仍然没做操作,我们使用类似 32x32 中的先复制再转置的方法,将 β[1][1](右下矩阵)转置好。
// 复制 α[1][1] 到 β[1][1]
// 依旧是先复制再转置以避免冲突不命中
// 若 i≠j,完全没有 MISS,因为 A、B 均在上个部分被读入缓存
// 若 i=j,因为上一部分最后是写 B 的最后一行,但是其他行都是正常的,所以读 A 时会出现 1 次冲突不命中,
// 读完 A 写 B 时,必定出现冲突不命中,每次循环 1 次 MISS
// 所以总计造成 0 / 5 次 MISS
for (int k = 4;k < 8;++k) {
a = A[i + k][j + 4];
b = A[i + k][j + 5];
c = A[i + k][j + 6];
d = A[i + k][j + 7];
B[j + k][i + 4] = a;
B[j + k][i + 5] = b;
B[j + k][i + 6] = c;
B[j + k][i + 7] = d;
}
// 转置 β[1][1]
// 全部 HIT
for (int k = 4;k < 8;++k) {
// 对角线不用交换
for (int l = 4;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}- 对于 i ≠ j:0 次 MISS
- 对于 i = j:5 次 MISS
最终,我们得到了满分的代码:
if (M == 64) {
// 因为每个 8*8 分块中,上半块和下半块会冲突不命中,所以再把每个 8*8 分块分成 4 个 4*4 分块
// 然后通过暂时性存储 β[1][0](左下块) 到 β[0][1](右上块) 来避免冲突不命中
// 若直接写到 β[1][0](左下块),则会写 B 的上半块(4*8) 和下半块(4*8) 时出现冲突不命中
// 特别的,对于 i=j 的情况,还是会出现冲突不命中,因为 A 本身和 B 就是冲突的
// 计算出的总 MISS 数为 (8+8)*56+(11+15+5)*8 = 1144 次,但是实际是 1148 次,应该又是程序调用的问题
for (int i = 0; i < N; i += 8) { // 当前行
for (int j = 0; j < M; j += 8) { // 当前列
// 先复制
for (int k = 0;k < 4;++k) {
// 从 A 中取 α[0][0]+α[0][1]的第 k 行,执行 4 次,即读出 A 的上半块,每次循环,读 A 都必然 MISS
// 所以总计 4 次 MISS。
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
e = A[i + k][j + 4];
f = A[i + k][j + 5];
g = A[i + k][j + 6];
h = A[i + k][j + 7];
// 转置前四个数到 β[0][0] 的第 k 列,4 次 MISS
// 若 i=j 还会因为上一步读 A 造成冲突不命中,所以额外造成 3 次冲突不命中。
B[j][i + k] = a;
B[j + 1][i + k] = b;
B[j + 2][i + k] = c;
B[j + 3][i + k] = d;
// 将后四个转置后,先复制到 β[0][1] 的第 k 列
// 可以避免此时去写 β[1][0] 的冲突不命中
B[j][i + k + 4] = e;
B[j + 1][i + k + 4] = f;
B[j + 2][i + k + 4] = g;
B[j + 3][i + k + 4] = h;
}
// 此时,已经转置完毕 β[0][0]
// 转置好的 β[1][0] 位于 β[0][1]
// * 对于 i ≠ j:4 + 4 = 8 次 MISS
// * 对于 i = j: 4 + 4 + 3 = 11 次 MISS
// ------- //
// 移动 β[0][1] 到 β[1][0]
// 同时将 α[1][0] 复制并转置到 β[0][1]
for (int k = 0;k < 4;++k) {
// 读 α[1][0] 的第 k 列,首次循环造成 4 次 MISS,后续循环均 HIT
// 对于 i=j 时,因为循环间读 B (见下一步,位于上半块)会造成 1 次冲突不命中,原有的一行缓存被驱逐
// 所以总计造成 4 / 7 次 MISS
e = A[i + 4][j + k];
f = A[i + 5][j + k];
g = A[i + 6][j + k];
h = A[i + 7][j + k];
// 复制 β[0][1] 的第 k 行,一定是行优先读,否则写的时候会出现额外的冲突不命中
// 若 i ≠ j 时因为上一部分最后写了这里,所以全部命中
// 若 i=j,每次循环都会因为上一步读 A 造成了冲突不命中,所以每次循环 1 次 MISS,总计 4 次 MISS
// 所以总计造成 0 / 4 次 MISS
a = B[j + k][i + 4];
b = B[j + k][i + 5];
c = B[j + k][i + 6];
d = B[j + k][i + 7];
// 将 α[1][0] 的第 k 列复制到 β[0][1] 的第 k 行,因为上一步读的时候已经完成缓存,所以写的时候不会 MISS
B[j + k][i + 4] = e;
B[j + k][i + 5] = f;
B[j + k][i + 6] = g;
B[j + k][i + 7] = h;
// 将 β[0][1] 的第 k 行复制到 β[1][0] 的第 k 行
// 注意你这里是按行读写的,所以对于所有情况,每次循环造成 1 次冲突不命中(上一步读上半块了,一定没缓存了)
// 所以总计造成 4 次 MISS
B[j + k + 4][i] = a;
B[j + k + 4][i + 1] = b;
B[j + k + 4][i + 2] = c;
B[j + k + 4][i + 3] = d;
}
// 这里我们已经将 β[1][0](左下矩阵)交换回正确的位置,以及转置了 β[0][1](右上矩阵)。
// * 对于 i ≠ j:4 + 4 = 8 次 MISS
// * 对于 i = j: 7 + 4 + 4 = 15 次 MISS
// ------- //
// 复制 α[1][1] 到 β[1][1]
// 依旧是先复制再转置以避免冲突不命中
// 若 i≠j,完全没有 MISS,因为 A、B 均在上个部分被读入缓存
// 若 i=j,因为上一部分最后是写 B 的最后一行,但是其他行都是正常的,所以读 A 时会出现 1 次冲突不命中,
// 读完 A 写 B 时,必定出现冲突不命中,每次循环 1 次 MISS
// 所以总计造成 0 / 5 次 MISS
for (int k = 4;k < 8;++k) {
a = A[i + k][j + 4];
b = A[i + k][j + 5];
c = A[i + k][j + 6];
d = A[i + k][j + 7];
B[j + k][i + 4] = a;
B[j + k][i + 5] = b;
B[j + k][i + 6] = c;
B[j + k][i + 7] = d;
}
// 转置 β[1][1]
// 全部 HIT
for (int k = 4;k < 8;++k) {
// 对角线不用交换
for (int l = 4;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
// * 对于 i ≠ j:0 次 MISS
// * 对于 i = j:5 次 MISS
}
}
}
运行:
make && ./test-trans -M 64 -N 64得到:
Summary for official submission (func 0): correctness=1 misses=1148距离理论最优值 1024(8x8 分块,64 个块,每个块 16 次 miss) 仍然有一定差距,但是已经很接近了,而且已经收获了满分。
如果你想继续优化,显然是要特别处理对角线上的块的,因为他们每次都会出现冲突不命中,所以可以通过先复制到一个临时块这样的方法来避免,这里就不展开了 (才不是懒得卷了)。
60x68#
测试指令:
make && ./test-trans -M 60 -N 68满分线:misses <= 1600。
首先尝试 4x4 分块:
if (M == 60) {
for (int i = 0; i < N; i += 4) { // 当前行
for (int j = 0; j < M; j += 4) { // 当前列
// 首先将 A[i][j]~A[i+3][j+3] 复制到 B[j][i]~B[j+3][i+3]
for (int k = 0;k < 4;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
}
// 转置 B
for (int k = 0;k < 4;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
}
运行:
make && ./test-trans -M 60 -N 68得到:
Summary for official submission (func 0): correctness=1 misses=1623发现似乎已经接近满分了啊?那我们只需要贪心地对大部分地方用 8x8 分块,再用 4x4 分块处理余下的部分就行了:
if (M == 60) {
// 行列都不整除 8,但正好可以避免冲突不命中
// 如果直接使用 4x4 分块,总 MISS 数为 1623,已经很接近满分
// 再次基础上,再贪心拆出一个 8x8 分块,然后用 4x4 解决剩余部分,即可拿到满分
// 总 MISS:1567
// 8x8 分块处理 64x56 的部分
for (int i = 0; i < 64; i += 8) {
for (int j = 0; j < 56; j += 8) {
for (int k = 0;k < 8;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
e = A[i + k][j + 4];
f = A[i + k][j + 5];
g = A[i + k][j + 6];
h = A[i + k][j + 7];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
B[j + k][i + 4] = e;
B[j + k][i + 5] = f;
B[j + k][i + 6] = g;
B[j + k][i + 7] = h;
}
// 转置 B
for (int k = 0;k < 8;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
// 4x4 处理剩余部分
for (int i = 0; i < N; i += 4) {
for (int j = 56; j < M; j += 4) {
for (int k = 0;k < 4;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
}
// 转置 B
for (int k = 0;k < 4;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
for (int i = 64; i < N; i += 4) {
for (int j = 0; j < 56; j += 4) {
for (int k = 0;k < 4;++k) {
a = A[i + k][j];
b = A[i + k][j + 1];
c = A[i + k][j + 2];
d = A[i + k][j + 3];
B[j + k][i] = a;
B[j + k][i + 1] = b;
B[j + k][i + 2] = c;
B[j + k][i + 3] = d;
}
// 转置 B
for (int k = 0;k < 4;++k) {
// 对角线不用交换
for (int l = 0;l < k;++l) {
a = B[j + k][i + l];
B[j + k][i + l] = B[j + l][i + k];
B[j + l][i + k] = a;
}
}
}
}
}
运行:
make && ./test-trans -M 60 -N 68得到:
Summary for official submission (func 0): correctness=1 misses=1567完美!下播!
Handin#
首先运行:
python driver.py得到结果:
Part A: Testing cache simulator
Running ./test-csim
Your simulator Reference simulator
Points (s,E,b) Hits Misses Evicts Hits Misses Evicts
3 (1,1,1) 9 8 6 9 8 6 traces/yi2.trace
3 (4,2,4) 4 5 2 4 5 2 traces/yi.trace
3 (2,1,4) 2 3 1 2 3 1 traces/dave.trace
3 (2,1,3) 694 453 449 694 453 449 traces/mem.trace
3 (2,2,3) 201 37 29 201 37 29 traces/trans.trace
3 (2,4,3) 212 26 10 212 26 10 traces/trans.trace
3 (5,1,5) 231 7 0 231 7 0 traces/trans.trace
6 (5,1,5) 265189 21777 21745 265189 21777 21745 traces/long.trace
27
TEST_CSIM_RESULTS=27
Your simulator Reference simulator
Points (s,E,b) Hits Misses Evicts Hits Misses Evicts
3 (1,1,1) 9 8 6 9 8 6 traces/yi2.trace
3 (4,2,4) 4 5 2 4 5 2 traces/yi.trace
3 (2,1,4) 2 3 1 2 3 1 traces/dave.trace
3 (2,1,3) 694 453 449 694 453 449 traces/mem.trace
3 (2,2,3) 201 37 29 201 37 29 traces/trans.trace
3 (2,4,3) 212 26 10 212 26 10 traces/trans.trace
3 (5,1,5) 231 7 0 231 7 0 traces/trans.trace
6 (5,1,5) 265189 21777 21745 265189 21777 21745 traces/long.trace
27
Part B: Testing transpose function
Running ./test-trans -M 32 -N 32 -t
Running ./test-trans -M 64 -N 64 -t
Running ./test-trans -M 60 -N 68 -t
Cache Lab summary:
Points Max pts Misses
Csim correctness 27.0 27
Trans perf 32x32 8.0 8 260
Trans perf 64x64 8.0 8 1148
Trans perf 60x68 10.0 10 1567
Total points 53.0 53注意阅读 README 中要求的代码格式:
- 缺少标题注释或标题注释不具描述性:扣 2 分
- 缺少函数头注释或函数头注释不具描述性:每处扣 1 分,最多扣 2 分
- 缩进不一致:扣 2 分
- 行长度严重超过 80 个字符(仅限极端情况):每处扣 1 分,最多扣 2 分
- 错误检查不充分:扣 1 分
- 任何其他严重影响可读性的问题:扣 2 分
本仓库内提供了一个 test-length.py 脚本,可以检查行长度是否超过 80 个字符,使用方法:
python test-length.py注意,提交前一定要先 make 并生成 handin.tar,然后改个名交了就行啦。
Other#
一些别的我觉得可能有用的教程:
NFLS-CHINA / CSAPP - Cache Lab 的更(最)优秀的解法 ↗:暂存想法的来源,很生动的图示。
孟永康 / 《深入理解计算机系统》配套实验:Cache Lab ↗:很好的解析了为什么尺寸变化会出现冲突。配有测试程序。